论文解读（DMVCJ）《Deep Embedded Multi-View Clustering via Jointly Learning Latent Representations and Graphs》

论文信息

论文标题：Deep Embedded Multi-View Clustering via Jointly Learning Latent Representations and Graphs
论文作者：Zongmo Huang、Yazhou Ren、Xiaorong Pu、Lifang He
论文来源：2022, ArXiv
论文地址：download
论文代码：download

1 Introduction

　　隶属于多视图聚类（MVC）算法，本文出发点是同时考虑特征信息和结构信息。

2 Method

　　问题声明：给定一个多视图数据集 $X=   \left\{X^{v}\right\}_{v=1}^{m}$，其中 $X^{v}=\left\{x_{1}^{v} ; x_{2}^{v} ; \ldots ; x_{n}^{v}\right\} \in   R^{n \times d^{v}}$，$d^{v}$ 是第 $v$ 个视图中特征向量的维数，$n$ 是实例数。我们的目标是将 $n$ 个实例划分为 $k$ 个簇。具体来说，我们的目标是通过联合学习不同视图之间的图结构和特征表示来更好地聚类结果。

　　总体框架：

　　

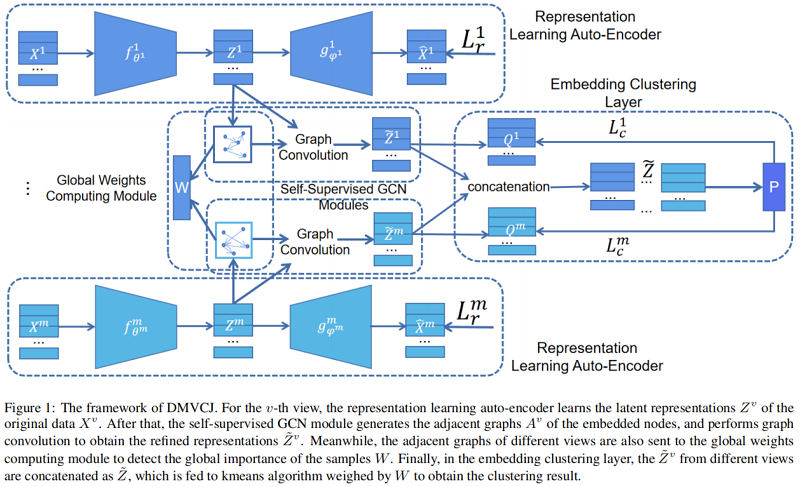
　　模型包括四个模块：

• • representation learning auto-encoder
  • self-supervised GCN module
  • global weights computing module
  • embedding clustering layer

2.1 Representation Learning Auto-Encoder

　　使用 $f_{\theta^{v}}^{v}$ 和 $g_{\phi^{v}}^{v}$ 来表示第 $v$ 个视图的编码器和解码器，其中 $\theta^{v}$ 和 $\phi^{v}$ 是可学习的参数。自编码器过程可以写为：

　　　　$z_{i}^{v}=f_{\theta_{v}}^{v}\left(x_{i}^{v}\right)\in R^{d_{v}} \quad\quad\quad(1)$

　　　　$\hat{x}_{i}^{v}=g_{\phi_{v}}^{v}\left(z_{i}^{v}\right)\in R^{d_{v}}\quad\quad\quad(2)$

　　重构损失：

　　　　$L_{r}^{v}=\sum\limits_{i=1}^{n}\left\|x_{i}^{v}-g_{\phi^{v}}^{v}\left(f_{\theta^{v}}^{v}\left(x_{i}^{v}\right)\right)\right\|_{2}^{2}\quad\quad\quad(3)$

2.2 Self-Supervised GCN Module

　　让 $Z^{v}=\left\{z_{1}^{v} ; z_{2}^{v} ; \ldots ; z_{n}^{v}\right\} \in R^{n \times d_{v}}$ 表示第$ $v$ 个视图中所有样本的潜在表示。

　　该模块首先根据嵌入表示的距离，利用kNN算法对相邻矩阵进行构造。然后对嵌入表示使用类似图卷积操作进一步处理，因此改进的嵌入表示 $\tilde{z}_{i}^{v}$ 计算为：

　　　　$\tilde{z}_{i}^{v}=\left(\tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}}\right)^{2} z_{i}^{v}\quad\quad\quad(4) $

　　其中

• • $\tilde{A}=I_{n}+A$
  • $\tilde{D}_{i i}=\sum_{j} \tilde{A}_{i j}$

2.3 Global Weights Computing Module

　　为了减轻噪声样本的影响，我们引入了一个由多个视图的相邻图得到的全局样本加权向量 $W=\left[w_{1}, w_{2}, \ldots, w_{n}\right]$ 。具体来说，对于第 $v$ 个视图中的第 $i$ 个节点，它在细化的相邻矩阵 $\tilde{A}^{v}$ 中的内度 $\eta_{i}^{v}$ 为：

　　　　$\eta_{i}^{v}=\sum\limits _{i} \tilde{A}_{i j}^{v}\quad\quad\quad(5)$

　　在2.2节模块中，$\tilde{A}^{v}$ 是由kNN算法导出的，对于第 $i$ 个节点，$\eta_{i}^{v}$ 的值表示在第 $v$ 个视图中视其为邻居的节点数（包括自身）。不难看出，$\eta_{i}^{v}$ 较高的节点通常位于簇的中心附近，而度值很小的节点可能是噪声点。将此理论扩展到多个视图，那么 $\eta_{i}=\sum_{v=1}^{m} \eta_{i}^{v}$ 的值反映了第 $i$ 个该样本的全局重要性。然后用一个简单的线性函数计算第 $i$ 个实例 $w_{i}$ 的全局权值：

　　　　$w_{i}=\min \left(\eta_{i} / \lambda, 1\right) \in(0,1]\quad\quad\quad(6)$

　　其中，$\lambda$ 被设置为 $\eta= [\eta(1), \eta(2), \ldots, \eta(n)]$ 的中值，确认至少有一半的样本被视为正常样本，并且所有的样本都可以参加训练。

2.4 Embedding Clustering Layer

　　在得到改进的嵌入表示 $\tilde{Z}^{v}=   \left\{\tilde{z}_{1}^{v} ; \tilde{z}_{2}^{v} ; \ldots ; \tilde{z}_{n}^{v}\right\} \in R^{n \times d_{v}}$ 后，应用嵌入聚类层 $c_{\mu^{v}}^{v}$ 计算第 $v$ 个视图中样本的聚类分配，其中 $\mu^{v}$ 表示可学习的聚类质心。具体来说，基于深度嵌入聚类模型中广泛使用的 $\text{Student's  t-distribution}$，在第 $v$ 个视图中，第 $i$ 个例子属于第 $j$ 个聚类的概率为：

　　　　$q_{i j}^{v}=c_{\mu^{v}}^{v}\left(\tilde{z}_{i}^{v}\right)=\frac{\left(1+\left\|\tilde{z}_{i}^{v}-\mu_{j}^{v}\right\|^{2}\right)^{-1}}{\sum_{j}\left(1+\left\|\tilde{z}_{i}^{v}-\mu_{j}^{v}\right\|^{2}\right)^{-1}}\quad\quad\quad(7) $

　　设 $Q^{v}=\left\{q_{1}^{v} ; q_{2}^{v} ; \ldots ; q_{n}^{v}\right\} \in R^{n \times k}$ 表示第 $v$ 个视图中所有样本的聚类分配。在本模块中，我们采用对偶自监督方法，即通过最小化单视图集群分配 $Q^{v}$ 和全局伪标签 $P$ 之间的差异来提高嵌入的特征在每个视图中的表示能力。

　　具体地说，$P$ 通过以下程序获得：首先，对于每个样本，将其嵌入的表示连接到所有视图中：

　　　　$\tilde{z}_{i}=\left[\tilde{z}_{i}^{1}, \tilde{z}_{i}^{2}, \ldots, \tilde{z}_{i}^{m}\right] \in R^{\sum_{v=1}^{m} d_{v}}\quad\quad\quad(8) $

　　然后，我们应用加权 kmeans 生成全局聚类质心 $ c_{j}$：

　　　　$\min _{c_{1}, c_{2}, \ldots, c_{k}} \sum_{i=1}^{n} \sum_{j=1}^{k} w_{i}\left\|\tilde{z}^{i}-c_{j}\right\|^{2}\quad\quad\quad(9) $

　　用 $\text{Student's t-distribution}$ 计算每个全局嵌入和每个集群质心之间的软分配 $s_{i j}$：

　　　　$s_{i j}=\frac{\left(1+\left\|\tilde{z}_{i}-c_{j}\right\|^{2}\right)^{-1}}{\sum_{j}\left(1+\left\|\tilde{z}_{i}-c_{j}\right\|^{2}\right)^{-1}} \quad\quad\quad(10) $

　　最后，通过以下方法计算全局伪标签 $P$：

　　　　$p_{i j}=\frac{\left(s_{i j}^{2} / \sum_{i} s_{i j}\right)}{\sum_{j}\left(s_{i j}^{2} / \sum_{i} s_{i j}\right)}\quad\quad\quad(11) $

　　其中，$P_{i j}$ 表示第 $i$ 个实例属于第 $j$ 个簇的概率。

　　在得到 $P$ 后，我们将每个视图的聚类损失 $L_{c}^{v}$ 定义为伪标签 $P$ 和 $Q^{v}$ 之间的Kullback-leibler散度(DKL)：

　　　　$L_{c}^{v}=D_{K L}\left(P \| Q^{v}\right)=\sum\limits_{i=1}^{n} w_{i} \sum\limits _{j=1}^{k} p_{i j} \log \frac{p_{i j}}{q_{v}^{i j}}\quad\quad\quad(12) $

　　通过优化 $Eq.12$，利用多个视图的信息提高每个视图嵌入自动编码器的表示能力，从而提高多视图聚类性能。

　　使用样本权重 $Eq.6$ 来细化重建损失 $Eq.3$，并与集群损失 $Eq.12$ 联合，每个视图中DMVCJ的损失函数为：

　　　　$L^{v}=\sum_{i=1}^{n} w_{i}\left(\left\|x_{i}^{v}-g_{\phi^{v}}^{v}\left(f_{\theta^{v}}^{v}\left(x_{i}^{v}\right)\right)\right\|_{2}^{2}+\gamma \sum_{j=1}^{k} p_{i j} \log \frac{p_{i j}}{q_{v}^{i j}}\right)\quad\quad\quad(13) $

　　其中，$\gamma$ 为一个趋势偏离系数。

2.5 Optimization

　　在训练过程结束后，我们再次计算伪标签 $P$，并得到第 $i$ 个样本的最终聚类分配 $y_i$：

　　　　$y_{i}=\underset{j}{\arg \max }\left(P_{i j}\right)\quad\quad\quad(14) $

　　算法如下：

　　

3 Experiement

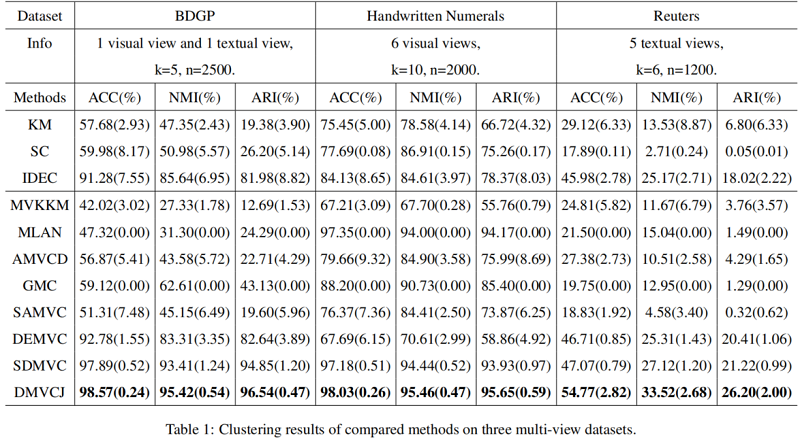
多视图聚类

　　

4 Conclusion

　　了解一下多视图聚类。

 

修改历史

2022-06-15 创建文章

 

论文解读目录