论文解读（gCooL）《Graph Communal Contrastive Learning》

论文信息

论文标题：Graph Communal Contrastive Learning
论文作者：Bolian Li, Baoyu Jing, Hanghang Tong
论文来源：2022, WWW
论文地址：download 
论文代码：download

1 Introduction

　　出发点：GCL 中节点级对比损失会有一定概率将同一社区中的节点视为负对，这是不合理的。

　　首先提出一种基于图结构信息学习社区划分的 Dense Community Aggregation（𝐷𝑒𝐶𝐴）算法。接下来，引入一种新的 Reweighted Self-supervised Cross-contrastive（𝑅𝑒𝑆𝐶）训练方案，将同一社区中的节点在表示空间中拉得更近。

　　本文框架：多视图对比。

2 Preliminaries

2.1 Similarity Measurement

　　Exponent cosine similarity:

　　　　$\delta_{c}\left(x_{1}, x_{2}\right)=\exp \left\{\frac{x_{1}^{T} x_{2} / \tau}{\left\|x_{1}\right\| \cdot\left\|x_{2}\right\|}\right\}  \quad\quad\quad(1)$

　　Gaussian RBF similarity:

　　　　$\delta_{e}\left(x_{1}, x_{2}\right)=\exp \left\{-\left\|x_{1}-x_{2}\right\|^{2} / \tau^{2}\right\} \quad\quad\quad(2)$

2.2 Community Detection

　　Modularity. 社区划分中常用的模块度 [42]：

　　　　$ m=\frac{1}{2 M} \sum\limits _{i, j}\left[A[i, j]-\frac{d_{i} d_{j}}{2 M}\right] r(i, j)  \quad\quad\quad(3)$

　　其中，$r(i, j)$ 代表着节点 $i$ 和 节点 $j$  是否属于同一个社区，模块度测量了每条边对局部边缘密度（local edge density  $\left(d_{i} d_{j} / 2 M\right)$）的影响。

　　Edge count function.我们定义了邻接矩阵上的边计数函数（edge count function）：

　　　　$E(C)=\sum\limits _{i, j} \mathbb{1}\left\{A^{C}[i, j] \neq 0\right\}   \quad\quad\quad(4)$

　　其中 $A^{C}$ 是社区 $C$ 的邻接矩阵。

　　Edge density function.边密度函数将真实边计数与给定社区 $C_{k}$ 中的最大可能边数进行比较：

　　　　${\large d(k)=\frac{E\left(C_{k}\right)}{\left|C_{k}\right|\left(\left|C_{k}\right|-1\right)}  }   \quad\quad\quad(5)$

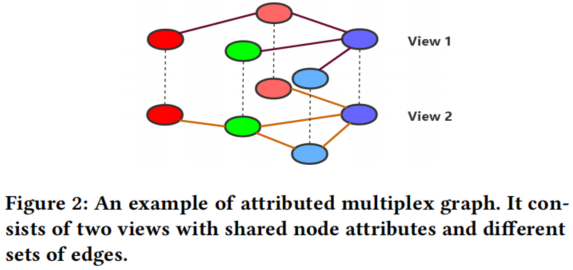
2.3 Attributed Multiplex Graph

　　Multiplex graphs 也被称为 multi-dimensional graphs [39]或 multi-view graphs[12,23,55]，它由多个单视图组成，具有共享的节点和属性，但具有不同的图结构]。

　　Formally, an attributed multiplex graph is  $\mathscr{G}=\left\{G^{1}, G^{2}, \ldots \ldots, G^{R}\right\}$, where  $R \in \mathbb{N}_{+} and each  G^{r}=\left(V, E^{r}\right)$  is an attributed graph. If the number of views  $R=1$, $\mathscr{G}=\left\{G^{1}\right\}$  is equivalent to the attributed graph  $G^{1}$ . We show an example of attributed multiplex graph in Fig.  2 . 

　　　　

3 Method

3.1 Dense Community Aggregation 

　　节点级GCL方法容易出现将结构相近的节点作为负样本配对的问题。

　　本文的方法受到图中的模块化[42]的启发，它测量了社区中的 local edge density 。然而，模块化很容易受到边[36]的变化的干扰，这限制了其在检测社区时的鲁棒性。

　　因此，本文目标是增强模块化的鲁棒性，并通过最大化每个社区的边缘密度来进一步扩展模块化，同时最小化不同社区之间的边缘密度。DeCA 通过端到端训练进行，如 Fig. 3 所示。

　　　　

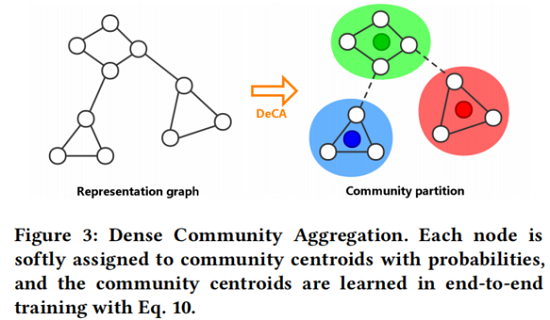
　　本文通过以端到端方式训练一个随机初始化的质心矩阵 $\Phi$ 来学习社区划分，其中每个 $\Phi[k,:]$ 代表第 $k$ 个社区的中心。

　　首先，将图中的每个节点以一定的概率分配给社区质心。具体地说，定义了一个社区分配矩阵 $\boldsymbol{R}$，其中每个 $\boldsymbol{R}[i,:]$ 都是一个标准化的相似度向量，度量第 $i$ 个节点和所有社区质心之间的距离。在形式上，$\boldsymbol{R}$ 是由

　　　　$\boldsymbol{R}=\text { normalize }\left(\delta\left(f_{\theta}(\boldsymbol{X}, \boldsymbol{A}), \boldsymbol{\Phi}\right)\right) \quad\quad\quad(6)$

　　其中，$\delta(\cdot)$ 为 $\text{2.1}$ 节中定义的相似度函数。$f_{\theta}(\cdot)$ 是参数为 $\theta$ 的图编码器，$normalize (\cdot)$ 通过将每个社区的概率除以所有概率之和来归一化，并保持每个 $i$ 的 $\sum_{j} R[i, j]=1$。

　　其次，采用了两个目标来训练社区划分：

　　社区内密度 （intra-community density）：

　　　　$D_{\text {intra }}=\frac{1}{N} \sum\limits _{i, j} \sum\limits_{k}[A[i, j]-d(k)] R[i, k] R[j, k]\quad\quad\quad(7)$

　　社区间密度（inter-community density ）：

　　　　$D_{\text {inter }}=\frac{1}{N(N-1)} \sum\limits_{i, j} \sum\limits_{k_{1} \neq k_{2}} A[i, j] R\left[i, k_{1}\right] R\left[j, k_{2}\right]  \quad\quad\quad(8)$

　　这两个目标测量了每条边对社区边密度（community edge density）的影响。具体来说，在 $Eq. 7$ 和 $Eq. 8$ 中、$A[i, j]-d(k)$ 和 $A[i, j]-0$ 表示真实局部密度 $(A[i, j])$ 和预期密度 $d(k)$ 之间的差距。通过最小化联合目标，将更新质心矩阵 $\Phi$，以达到合理的社区划分：

　　　　$l_{D e C A}(R)=\lambda_{w} D_{\text {inter }}-D_{\text {intra }}   \quad\quad\quad(9)$

　　其中 $\lambda_{w}$ 是系数。此外，为提高计算效率，在实际实现中稍微修改了 $l_{D e C A}$ 的形式。

　　最后，结合了两个图视图的 $l_{D e C A}$ 目标，并同时对它们进行密集的社区聚合：

　　　　$L_{D e C A}=\frac{1}{2}\left[l_{D e C A}\left(R^{1}\right)+l_{D e C A}\left(R^{2}\right)\right]  \quad\quad\quad(10)$

3.2 Reweighted Self-supervised Cross-contrastive Training

　　在本节中，提出 重加权自监督交叉对比（$ReSC$ ）训练方案。

　　首先应用图数据增强来生成两个图视图，然后同时应用 节点对比 和 社区对比 来考虑节点级和社区级的信息。我们引入 node-community 对作为额外的负样本，以解决与负样本在相同的社区中配对节点的问题。

3.2.1 Graph augmentation

　　属性掩藏

　　　　$\widetilde{X}=[X[1,:] \odot \boldsymbol{m} ; \boldsymbol{X}[2,:] \odot \boldsymbol{m} ; \ldots \ldots ; \boldsymbol{X}[N,:] \odot \boldsymbol{m}]^{\prime} \quad\quad\quad(11)$

　　其中，$m[i] \sim \text { Bernoulli }\left(1-p_{v}\right)$，$\odot $ 代表着 Hadamard product 。

　　边丢弃

　　有概率地从原始边集 $E$ 中随机删除边来生成增广边集 $\widetilde{E}$。

　　　　$P\left\{\left(v_{1}, v_{2}\right) \in \widetilde{E}\right\}=1-p_{e}, \forall\left(v_{1}, v_{2}\right) \in E \quad\quad\quad(12)$

　　上述两种数据增强，分别定义为 $t^{1}, t^{2} \sim T$。

　　使用上述两种数据增强生成两个视图：

　　　　$\left(X^{1}, A^{1}\right)=t^{1}(X, A)$

　　　　$\left(X^{2}, A^{2}\right)=t^{2}(X, A)$

　　最后后通过 GCN 编码器获得他们的表示：

　　　　$Z^{1}=f_{\theta}\left(X^{1}, A^{1}\right)$

　　　　$Z^{2}=f_{\theta}\left(X^{2}, A^{2}\right)$

3.2.2 Node contrast

　　在生成两个视图后，同时使用节点对比和社区对比来学习节点表示。

　　本文引入了一个基于InfoNCE[43] 的对比损失来做节点级对比损失：

　　　　$I_{N C E}\left(Z^{1} ; Z^{2}\right)=-\log \sum\limits_{i} \frac{\delta\left(Z^{1}[i,:], Z^{2}[i,:]\right)}{\sum_{j} \delta\left(Z^{1}[i,:], Z^{2}[j,:]\right)} \quad\quad\quad(13)$

　　对这两个视图对称地应用节点对比损失：

　　　　$L_{n o d e}=\frac{1}{2}\left[I_{N C E}\left(Z^{1} ; Z^{2}\right)+I_{N C E}\left(Z^{2} ; Z^{1}\right)\right]\quad\quad\quad(14)$

　　它在两个视图中区分负对，并强制最大化正对[35]之间的一致性。

3.2.3 Community contrast

　　首先，用 $Eq.10$ 训练随机初始化的社区质心矩阵 $\Phi$，得到社区质心。

　　其次，采用一个重新加权的交叉对比目标，将一个视图的节点表示与另一个视图的社区质心进行对比（一种交叉对比的方式）。在形式上，社区对比是由

　　　　${\large \begin{array}{l}l_{\text {com }}(Z, \Phi)=-\log \sum_{i} \frac{\delta\left(Z[i,:], \Phi\left[k_{i},:\right]\right)}{\delta\left(Z[i,:], \Phi\left[k_{i},:\right]\right)+\sum_{k_{i} \neq k} w(i, k) \cdot \delta(Z[i,:], \Phi[k,:])}\end{array}} \quad\quad\quad(15)$

　　其中：

• • $w(i, k)=\exp \left\{-\gamma\|Z[i,:]-\Phi[k,:]\|^{2}\right\}$ 是RBF的权值函数；

　　在这一目标中，相同社区内的节点表示的相似性最大化，因为它们与相同的质心呈正对比，而在不同的社区中，节点表示被负对比分开。

　　同样，对称地计算了生成的两个视图的对比目标：

　　　　$L_{\text {com }}=\frac{1}{2}\left[l_{\text {com }}\left(Z^{1}, \Phi^{2}\right)+l_{\text {com }}\left(Z^{2}, \Phi^{1}\right)\right]\quad\quad\quad(16)$

3.2.4 Joint objective

　　本文提出用 $\alpha$-衰减系数将 $L_{n o d e}$, $L_{D e C A}$ 和 $L_{\text {com }}$ 结合成一个联合目标：

　　　　$L=L_{\text {node }}+\alpha(t) L_{D e C A}+[1-\alpha(t)] L_{\text {com }}\quad\quad\quad(17)$

　　其中，系数 $\alpha(t)=\exp \{-t / \eta\}$ 会随着训练的进行而顺利衰减（ $t$ 为 epoch）。

　　实验观察到，通过 $DeCA$ 训练，社区分区将稳定在几百个 epoch 内，而 $g CooL$ 模型的训练通常需要数千个 epoch。为此，首先将  $\alpha$-衰减主要应用于训练社区划分，并逐步将重点转移到学习节点表示上。

　　综上所述，$ReSC$ 的训练过程如 Algorithm 1 所示。

　　 

3.3 Adaptation to Multiplex graphs

　　将 $gCooL$ 框架用于多重图，并对训练和推理过程进行了一些修改。

3.3.1 Training

　　在多重图中，不再需要通过图增强来生成图视图，因为多重图中的不同视图自然是多重查看的数据。我们建议在每对视图上检测社区（𝐷𝑒𝐶𝐴）和学习节点表示（𝑅𝑒𝑆𝐶）。改进后的训练过程如 Algorithm 2 所示。

　　

3.3.2 Inference

　　在推理时，我们建议通过分类器融合（后集成方式）结合每个视图的分类结果：给定 $R$ 独立分类器的结果，我们根据每个分类器的置信度(即输出softmax分布[17]的最大值)对最终预测进行标记。我们选择置信度最高的结果作为最终的预测。

4 Experiments

4.1 Experimental Setup

4.1.1 datasets

　　

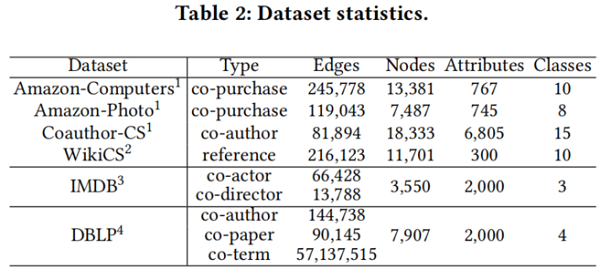
4.1.2 Evaluation protocol

　　对于节点分类任务，我们用 Micro-F1 和 Macro-F1 分数来衡量性能。

　　对于节点聚类任务，我们使用归一化互信息(NMI)评分来衡量性能：

　　　　$N M I=2 I(\hat{Y} ; Y) /[H(\hat{Y})+H(Y)]$

　　其中，$\hat{Y}$ 和 $Y$ 分别为预测的聚类索引和类标签。

　　Adjusted Rand Index (ARI): 

　　　　$A R I=R I-\mathbb{E}[R I] /(\max \{R I\}-\mathbb{E}[R I])$

　　其中， $RI$ 是RandIndex[51]，它测量两个集群索引和类标签之间的相似性。

4.1.3 Baselines

On single-view graphs

• 1) traditional methods including node2vec [13] and DeepWalk [48],
• 2) supervised methods including GCN [28]
• 3) unsupervised methods including MVGRL [16], DGI [59], HDI [21], graph autoencoders (GAE and VGAE) [29] and GCA [78].

On multiplex graphs

• 1) methods with single-view representations including node2vec [13], DeepWalk [48], GCN [28] and DGI [59]
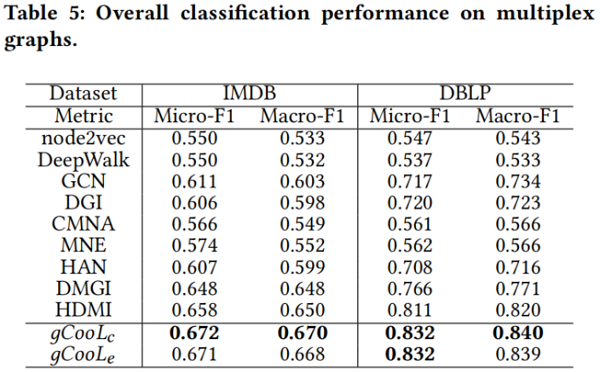
• 2) methods with multi-view representations including CMNA [7], MNE [70], HAN [62], DMGI [44] and HDMI [21].

　　此外，我们比较了不同的聚类基线，包括K-means、光谱双聚类(SBC)[30]和模块化[42]，以显示我们提出的 𝐷𝑒𝐶𝐴(指数余弦相似度 $DeCA_{c}$ 和高斯RBF相似度  $D e C A_{e}$) 的有效性。

4.2 Quantitative Results 

node classification on single-view graphs (Table 3)

　　

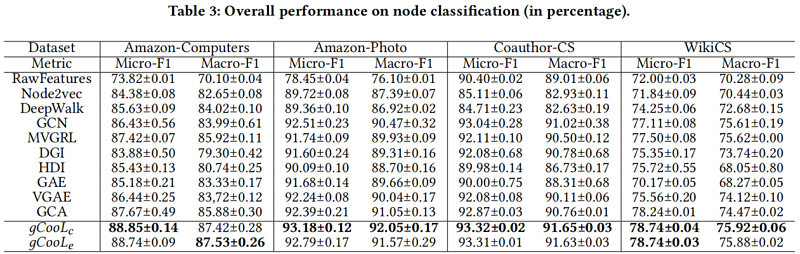
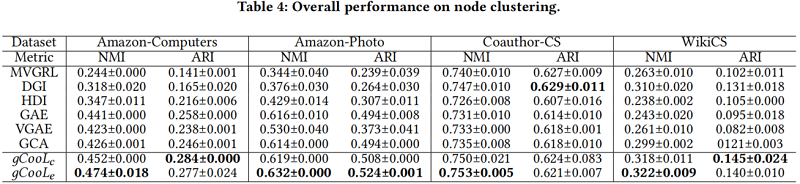
node clustering on single-view graphs (Table 4)

　　

node classification on multiplex graphs (Table 5)

　　

Performance on node clustering

　　

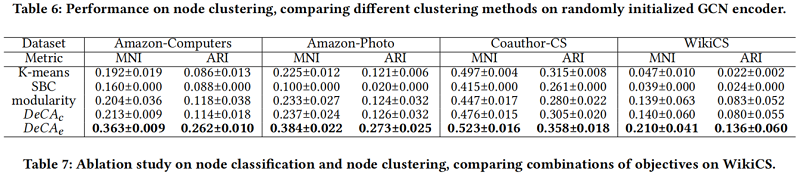
Ablation study

　　

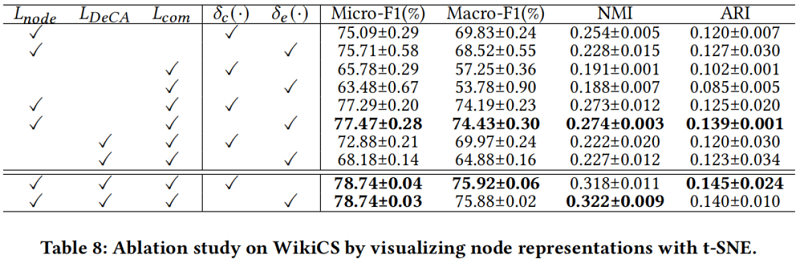
4.3 Visual Evaluations

　　我们通过可视化所分配社区的边缘密度和类熵来说明𝐷𝑒𝐶𝐴的重要性。我们评估每个检查点五次，并显示其平均值和偏差。我们将结果与传统的聚类方法(K-means和光谱双聚类[30])和前模块化[42]进行了比较。我们还可视化了消融研究的节点表示。

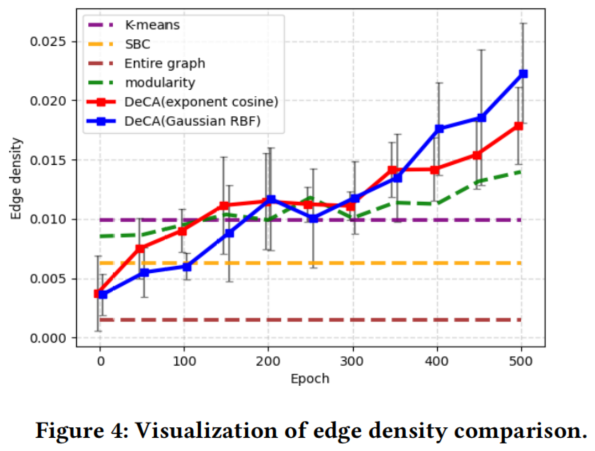
4.3.1 Edge density

　　边缘密度是基于 $\text{Eq.5}$、按所有社区的平均密度计算： 

　　　　$E D=\frac{1}{K} \sum\limits _{k=1}^{K} d(k)  \quad\quad\quad(18)$

　　它被用来衡量𝐷𝑒𝐶𝐴如何学习社区分区，从而使群落内密度最大化( Section 3.1)。从Fig4可以看出，经过几百个 epochs 后，𝐷𝑒𝐶𝐴的性能稳定地优于其他聚类方法。

　　

4.3.2 Class entropy

　　类熵是对一个社区中类标签的同质性（一个社区包含一个主要类或具有低熵的程度）的度量。我们认为，一个好的社区分区应该区分结构上分离的节点，换句话说，就是区分不同类的节点。类熵计算为所有社区中类标签的平均熵：

　　　　$C H=-\frac{1}{K} \sum\limits _{k=1}^{K} \sum\limits_{c} P_{k}(c) \log P_{k}(c) \quad\quad\quad(19)$

　　其中，$P_{k}(c)$ 为第 $k$ 个社区中第 $c$ 类的出现频率。从 $Fig. 5$ 可以看出，经过几百个 epochs 后，𝐷𝑒𝐶𝐴的性能稳定地优于其他聚类方法。

4.3.3 Visualization of node representations

　　为了解节点表示是如何分布的，使用 t-SNE[57] 来减少节点表示的维数以进行可视化。

　　当应用 $𝐿_{𝐷𝑒𝐶𝐴}$ 和 $𝐿_{com}$ 时，每个类的节点表示分别分布更大，这说明了我们所提出的方法的有效性。结果如 Table 8 所示。

　　

6 Conclusion

　　在本文中，我们提出了一种新的图社区对比学习（𝑔𝐶𝑜𝑜𝐿）框架，通过密集的社区聚合（𝐷𝑒𝐶𝐴）算法来学习结构相关社区的社区划分，并通过考虑社区结构的重加权自监督交叉对比（𝑅𝑒𝑆𝐶）训练方案来学习图的表示。所提出的𝑔𝐶𝑜𝑜𝐿在多个任务上始终达到了最先进的性能，并且可以自然地适应于多路图。我们表明，社区信息有利于图表示学习的整体性能。

Appendix

　　在 𝐷𝑒𝐶𝐴，由于边密度依赖于社区的选择，因此社区内密度目标的计算代价高昂且难以向量化。为了解决这个问题，我们推导了 $𝐷_{𝑖𝑛𝑡𝑟𝑎}$ 的一个下界：

　　　　$\begin{aligned}D_{\text {intra }} & \geq \frac{1}{N} \sum_{i, j} \sum_{k}\left[A[i, j]-\max _{\kappa}\{d(\kappa)\}\right] R[i, k] R[j, k] \\&=\frac{1}{N} \sum_{i, j} \sum_{k} \widetilde{A}[i, j] R[i, k] R[j, k] \\&=\widetilde{D}_{\text {intra }}\end{aligned}$

　　其中，$\widetilde{\boldsymbol{A}}=\boldsymbol{A}-\max _{\kappa} d(\kappa) \boldsymbol{I}$ 为扩展邻接矩阵，$\widetilde{D}_{\text {intra }}=\inf D_{\text {intra }}$ 为下界。我们使用 $\widetilde{D}_{\text {intra }}$ 来代替 $\text{Eq.9}$ 中的 $D_{\text {intra }}$.

　　接下来，我们利用社区密度矩阵 $F=R^{\prime} A R$ 和 $\widetilde{F}=R^{\prime} \widetilde{A} R$ 对目标 $D_{\text {inter }}$ 和 $\widetilde{D}_{\text {intra }}$ 进行向量化。$F$ 的条目是 $F[u, v]=\sum_{i} R[i, u] \cdot(A R)[i, v]=\sum_{i, j} A[i, j] R[i, u] R[j, v]$，它自然符合 $\text{Eq.7}$ 和 $\text{Eq.8}$ 的形式。因此，这两个目标可以被重新形式定义为

　　　　$\tilde{D}_{\text {intra }}=\frac{1}{N} \operatorname{tr}(\widetilde{F})\quad\quad\quad(21)$

　　　　$D_{\text {inter }}=\frac{1}{N(N-1)}\left[\sum\limits _{i, j} F[i, j]-\operatorname{tr}(F)\right]\quad\quad\quad(22)$

　　最后，向量化的 𝐷𝑒𝐶𝐴 目标为:

　　　　$\begin{aligned}l_{D e C A}(R) &=\lambda_{w} D_{\text {inter }}-\widetilde{D}_{i n t r a} \\&=\frac{\lambda_{w}}{N(N-1)}\left[\sum\limits _{i, j} F[i, j]-\operatorname{tr}(F)\right]-\frac{1}{N} \operatorname{tr}(\widetilde{F})\end{aligned}\quad\quad\quad(23)$