论文解读（AGE)《Adaptive Graph Encoder for Attributed Graph Embedding》

论文信息

论文标题：Adaptive Graph Encoder for Attributed Graph Embedding
论文作者：Gayan K. Kulatilleke, Marius Portmann, Shekhar S. Chandra
论文来源：2020, KDD
论文地址：download
论文代码：download

1 Introduction

　　基于 GCN 的方法有三个主要缺点：

• • 图卷积滤波器和权值矩阵的纠缠会损害其性能和鲁棒性；
  • 图卷积滤波器是广义拉普拉斯平滑滤波器的特殊情况，但没有保持最优的低通特性；
  • 现有算法的训练目标通常是恢复邻接矩阵或特征矩阵，处理与现实不符；

　　AGE 由两个模块组成：

• • 拉普拉斯平滑滤波器；
  • 自适应编码器；

　　首先，一个GCN 编码器由多个图卷积层组成，每一层包含一个图卷积滤波器 $H$、一个权值矩阵 ($W_1$、$W_2$) 和一个激活函数。[35] 证明，滤波器和权值矩阵的纠缠并没有为半监督图表示学习提供性能增益，甚至损害了训练效率，因为它加深了反向传播的路径。

　　 

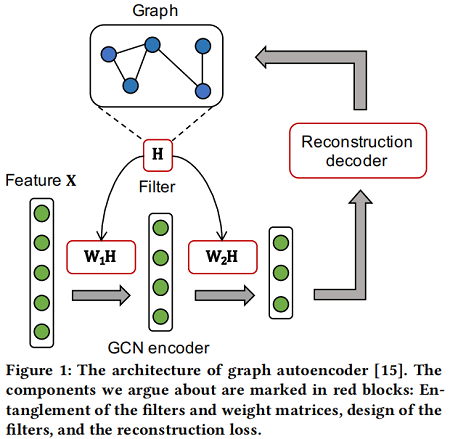
　　其次，考虑图卷积滤波器， [18] 在理论上表明，它们实际上是应用于低通去噪的特征矩阵上的拉普拉斯平滑滤波器 [28]。本文证明了现有的图卷积滤波器并不是最优的低通滤波器，因为它们不能过滤某些高频噪声。因此，它们不能达到最好的平滑效果。

　　最后，本文认为这些算法的训练目标（重建邻接矩阵 [23,31] 或特征矩阵 [24,32]）与现实应用不兼容。具体来说，重构邻接矩阵是将邻接矩阵设为地面真值成对相似度，但不适合于缺乏特征信息的情况。然而，恢复特征矩阵将迫使模型记住特征中的高频噪声，因此也是不合适的。

2 Method

　　整体框架：

　　 

　　组成部分：

• • a Laplacian smoothing filter
    • Laplacian Smoothing Filter: The designed filter $H$ serves as a low-pass filter to denoise the high-frequency components of the feature matrix  $\mathrm{X}$ . The smoothed feature matrix  $\tilde{\mathrm{X}}$  is taken as input of the adaptive encoder.
      
  • an adaptive encoder
    • Adaptive Encoder: To get more representative node embeddings, this module builds a training set by adaptively selecting node pairs which are highly similar or dissimilar. Then the encoder is trained in a supervised manner.　　

2.1 Laplacian Smoothing Filter

　　基本假设：图上邻居节点具有相似性。

2.1.1 Analysis of Smooth Signals

　　从图信号处理的角度来解释图平滑。以 $\mathbf{x} \in \mathbb{R}^{n}$ 作为图信号，每个节点被分配一个值向量。为测量图信号 $x$ 的平滑度，可以计算出图拉普拉斯矩阵 $L$ 和 $x$ 上的瑞利商：

　　　　${\large R(\mathbf{L}, \mathbf{x})=\frac{\mathbf{x}^{\boldsymbol{\top}} \mathbf{L} \mathbf{x}}{\mathbf{x}^{\top} \mathbf{x}}=\frac{\sum\limits_{(i, j) \in \mathcal{E}}\left(x_{i}-x_{j}\right)^{2}}{\sum\limits_{i \in \mathcal{V}} x_{i}^{2}}}  \quad\quad\quad(1)$

　　PS：拉普拉斯矩阵的性质

　　$\begin{aligned}f^{T} L f &=f^{T} D f-f^{T} W f \\&=\sum \limits_{i=1}^{N} d_{i} f_{i}^{2}-\sum \limits_{i=1}^{N} \sum \limits_{j=1}^{N} w_{i j} f_{i} f_{j} \\&=\frac{1}{2}\left(\sum \limits_{i=1}^{N} d_{i} f_{i}^{2}-2 \sum \limits_{i=1}^{N} \sum \limits_{j=1}^{N} w_{i j} f_{i} f_{j}+\sum \limits_{j=1}^{N} d_{j} f_{j}^{2}\right) \\&=\frac{1}{2}\left(\sum \limits_{i=1}^{N} \sum \limits_{j=1}^{N} w_{i j} f_{i}^{2}-2 \sum \limits_{i=1}^{N} \sum \limits_{j=1}^{N} w_{i j} f_{i} f_{j}+\sum \limits_{i=1}^{N} \sum \limits_{j=1}^{N} w_{i j} f_{j}^{2}\right) \\&=\frac{1}{2} \sum \limits_{i=1}^{N} \sum \limits_{j=1}^{N} w_{i j}\left(f_{i}-f_{j}\right)^{2}\end{aligned}$

　　$\text{Eq.1}$ 显然是 $x$ 的标准化方差分数。平滑信号应该在相邻节点上分配相似的值。因此，假设瑞利商较低的信号更平滑，接着给出特征向量 $u_i$ 的光滑性度量：

　　　　${\large R\left(\mathbf{L}, \mathbf{u}_{i}\right)=\frac{\mathbf{u}_{i}^{\top} \mathbf{L} \mathbf{u}_{i}}{\mathbf{u}_{i}^{\top} \mathbf{u}_{i}}=\lambda_{i}}  \quad\quad\quad(2)$

　　$\text{Eq.2}$ 表示平滑的特征向量与较小的特征值相关联，即较低的频率。因此，基于$\text{Eq.1}$、$\text{Eq.2}$   $L$ 分解信号 $x$):

　　　　$\mathbf{x}=\mathbf{U p}=\sum\limits _{i=1}^{n} p_{i} \mathbf{u}_{i} \quad\quad\quad(3)$

　　其中 $p_{i}$ 是特征向量 $\mathbf{u}_{i}$ 的系数，那么 $x$ 的平滑度是：

　　　　${\large R(\mathbf{L}, \mathbf{x})=\frac{\mathbf{x}^{\top} \mathbf{L} \mathbf{x}}{\mathbf{x}^{\top} \mathbf{x}}=\frac{\sum \limits_{i=1}^{n} p_{i}^{2} \lambda_{i}}{\sum \limits_{i=1}^{n} p_{i}^{2}}  }   \quad\quad\quad(4)$

　　因此，为获得更平滑的信号，本文滤波器的目标是在保留低频分量的同时滤掉高频分量。

2.1.2 Generalized Laplacian Smoothing Filter

　　如[28]所述，广义拉普拉斯平滑滤波器为：

　　　　$\mathbf{H}=\mathbf{I}-k \mathbf{L}    \quad\quad\quad(5)$

　　采用 $\mathbf{H}$ 作为滤波器矩阵，滤波后的信号 $\tilde{\mathbf{x}}$ 为：

　　　　${\large \tilde{\mathbf{x}}=\mathbf{H x}=\mathbf{U}(\mathbf{I}-k \Lambda) \mathbf{U}^{-1} \mathbf{U p}=\sum \limits_{i=1}^{n}\left(1-k \lambda_{i}\right) p_{i} \mathbf{u}_{i}=\sum \limits_{i=1}^{n} p^{\prime} \mathbf{u}_{i}  } \quad\quad\quad(6)$

　　因此，为实现低通滤波(low-pass filtering)，频率响应函数 $1-k \lambda$ 应是一个递减和非负函数。叠加 $t$ 次拉普拉斯平滑滤波器，将滤波后的特征矩阵 $\tilde{\mathbf{X}}$ 表示为

　　　　$\tilde{\mathbf{X}}=\mathbf{H}^{t} \mathbf{X}   \quad\quad\quad(7)$

　　请注意，该过滤器根本是非参数化的。

2.1.3  The Choice of k

　　在实践中，使用重整化技巧 $\tilde{\mathrm{A}}=\mathrm{I}+\mathbf{A}$，采用对称归一化图拉普拉斯矩阵

　　　　$\tilde{\mathbf{L}}_{s y m}=\tilde{\mathbf{D}}^{-\frac{1}{2}} \tilde{\mathbf{L}} \tilde{\mathbf{D}}^{-\frac{1}{2}}   \quad\quad\quad(8)$

　　此时滤波器为：

　　　　$\mathbf{H}=\mathbf{I}-k \tilde{\mathbf{L}}_{s y m}  \quad\quad\quad(9)$

　　注意，如果设置 $k=1$，滤波器将成为 GCN 滤波器。
　　为选择最优 $k$，需要计算特征值 $\tilde{\Lambda}$ 的分布（由 $\tilde{\mathbf{L}}_{s y m}=\tilde{\mathbf{U}} \tilde{\Lambda} \tilde{U}^{-1}$ 分解得到）。

　　$\tilde{\mathbf{x}}$ 的平滑度是

　　　　${\large R(\mathbf{L}, \tilde{\mathbf{x}})=\frac{\tilde{\mathbf{x}}^{\top} \mathbf{L} \tilde{\mathbf{x}}}{\tilde{\mathbf{x}} \boldsymbol{\tilde { \mathbf { x } }}}=\frac{\sum_{i=1}^{n} p^{\prime}{ }_{i}^{2} \lambda_{i}}{\sum_{i=1}^{n} p^{\prime}{ }_{i}^{2}}}  \quad\quad\quad(10)$

　　因此，$p^{\prime}{ }_{i}^{2}$ 应随 $\lambda_{i}$ 的增加而减少。将最大特征值表示为 $\lambda_{\max }$，理论上，如果 $k>1 / \lambda_{\max }$ ，滤波器在 $\left(1 / k, \lambda_{\max }\right]$ 内不是低通，因为 $p^{\prime}{ }_{i}^{2}$ 在这个间隔内增加；如果 $k<1 / \lambda_{\max }$ 该滤波器不能使去出高频噪声部分。因此，$k=1 / \lambda_{\max }$ 是最优选择。

　　[7] 证明了拉普拉斯特征值的范围在 $\text{0~2}$ 之间，因此GCN滤波器在 $(1,2]$ 区间内不是低通的。工作 [31] 相应地选择了 $k=1/2$，然而，我们的实验表明，在重整化后，最大特征值 $\lambda_{\max }$ 将缩小到 $3/2$ 左右，这使得 $1/2$ 不是最优。在实验中，我们计算每个数据集的 $\lambda_{\max }$，并设置 $k=1 / \lambda_{\max }$，并进一步分析了不同 $k$ 值的影响。

3 Adaptive Encoder

　　通过 $t$ 层拉普拉斯平滑过滤，输出特征更平滑，保持丰富的属性信息。本文自适应地选择高相似度的节点对作为正训练样本，而低相似度的节点对作为负训练样本。

　　给定过滤后的节点特征 $\tilde{\mathbf{X}}$，节点嵌入由线性编码器 $f$ 进行编码：

　　　　$\mathbf{Z}=f(\tilde{\mathbf{X}} ; \mathbf{W})=\tilde{\mathbf{X}} \mathbf{W}  \quad\quad\quad(11)$

　　其中，$\mathbf{W}$ 是权重矩阵。然后，为度量节点的成对相似度，利用余弦相似度。相似度矩阵 $S$ 为：

　　　　$\mathrm{S}=\frac{\mathrm{ZZ}^{\boldsymbol{T}}}{\|\mathrm{Z}\|_{2}^{2}}   \quad\quad\quad(12)$

　　接下来，我们将详细描述我们的训练样本选择策略。

3.1 Training Sample Selection.

　　在计算相似矩阵后，对相似序列按降序排列。这里 $r_{i j}$ 是节点对的排序位置  $\left(v_{i}, v_{j}\right)$。然后将正样本的最大排序位置设为 $r_{p o s}$，将负样本的最小排序位置设为 $r_{n e g}$。因此，为节点对 $\left(v_{i}, v_{j}\right)$ 生成的标签为

　　$l_{i j}=\left\{\begin{array}{ll}1 & r_{i j} \leq r_{p o s} \\0 & r_{i j}>r_{n e g} \\\text { None } & \text { otherwise }\end{array}\right.   \quad\quad\quad(13)$

　　这样，构造了一个包含  $r_{\text {pos }}$  个正样本和  $n^{2}-r_{n e g}$  个负样本的训练集。在第一次构造训练集时，由于编码器没有被认训练， 直接使用平滑的特征来初始化  $\mathbf{S}$  :

　　　　$\mathbf{S}=\frac{\widetilde{\mathbf{X}} \widetilde{\mathbf{X}}^{\mathbf{T}}}{\|\widetilde{\mathbf{X}}\|_{2}^{2}}   \quad\quad\quad(14)$

　　构造好训练集后，可以用监督的方式训练编码器。在真实世界的图中，不相似的节点对总是远远多于正节点对，因此在训 练集中选择多于  $r_{p o s}$  个负样本。为了平衡正/负样本，在每次迭代中随机选择  $r_{p o s}$  个负样本。平衡训练集用  $\mathcal{O}$  表示。因 此，交叉熵损失表示如下:

　　　　$\mathcal{L}=\sum \limits_{\left(v_{i}, v_{j}\right) \in O}-l_{i j} \log \left(s_{i j}\right)-\left(1-l_{i j}\right) \log \left(1-s_{i j}\right)   \quad\quad\quad(15)$

3.2 Thresholds Update

　　本文为 $r_{p o s}$ 和 $r_{n e g}$ 设计了一个特定的更新策略来控制训练集的大小。在训练开始时，选择更多的样本为编码器寻找粗化的聚类。之后，保留具有更高置信度的样本进行训练，将迫使编码器捕获细化的聚类。

　　在实践中，随着训练过程的进行，$r_{\text {pos }}$ 减少，而 $r_{n e g}^{s t}$ 呈线性增加。将初始阈值设置为 $r_{\text {pos }}^{s t}$ 和 $r_{n e g}^{s t}$，最终阈值设置为 $r_{\text {pos }}^{e d}$ 和 $r_{n e g}^{e d}$ 。有 $r_{\text {pos }}^{e d} \leq r_{\text {pos }}^{s t}$ 和 $r_{n e g}^{e d} \geq r_{\text {neg. }}^{s t}$。假设阈值被更新为 $T$次，我们将更新策略表示为

　　　　${\large r_{\text {pos }}^{\prime}=r_{p o s}+\frac{r_{\text {pos }}^{e d}-r_{\text {pos }}^{s t}}{T}}     \quad\quad\quad(16)$

　　　　${\large r_{n e g}^{\prime}=r_{n e g}+\frac{r_{n e g}^{e d}-r_{n e g}^{s t}}{T}}      \quad\quad\quad(17)$

　　随着训练过程的进行，每次阈值更新时，都会重建训练集并保存嵌入。

　　对于节点聚类，我们对保存嵌入的相似矩阵进行谱聚类[22]，利用戴维斯堡丁索引[8](DBI)选择最佳时期，在没有标签信息的情况下测量聚类质量。对于链路预测，我们在验证集上选择执行得最好的历元。Algorithm 1 给出了计算嵌入矩阵 $Z$ 的总体过程。

　　

4 Experiments

数据集

　　

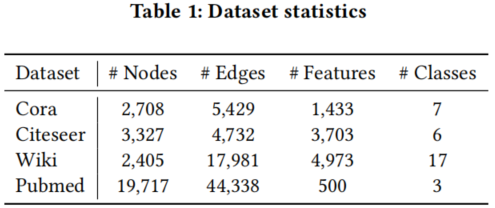
节点聚类

　　 

-----------------------------------------------------------------------------------------------------

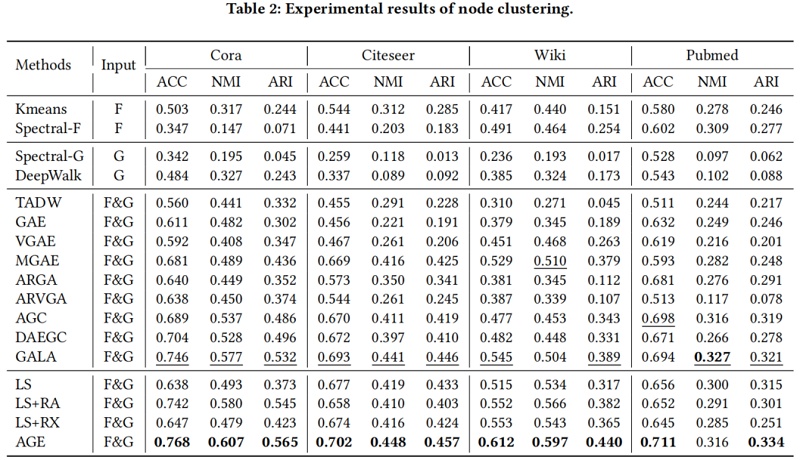
https://zhuanlan.zhihu.com/p/440760513

https://zhuanlan.zhihu.com/p/432080955