论文解读（FDGATII）《FDGATII : Fast Dynamic Graph Attention with Initial Residual and Identity Mapping》

论文信息

论文标题：FDGATII : Fast Dynamic Graph Attention with Initial Residual and Identity Mapping
论文作者：Gayan K. Kulatilleke, Marius Portmann, Ryan Ko, Shekhar S. Chandra
论文来源：2021, arXiv
论文地址：download 
论文代码：download 

1 Introduction

　　图神经网络引入图结构存在的问题：

• • oversmoothing
  • noisy neighbours (heterophily)
  • the suspended animation problem

2 Related Work

2.1 GCNII

　　GCNII 将 GCN 扩展到一个深度模型，使 GCN 能够用两种简单的技术来表示任意系数的 $K$ 阶多项式滤波器：初始残差连接和恒等式映射。在形式上，我们将GCNII的第 $l$ 层定义为：

　　　　$\mathbf{H}^{l+1}=\sigma\left(\left(\left(1-\alpha_{l}\right) \overline{\mathbf{P}} \mathbf{H}^{l}+\alpha_{l} \mathbf{H}^{0}\right)\left(\left(1-\beta_{l}\right) \mathbf{I}_{n}+\beta_{l} \mathbf{W}^{l}\right)\right)     \quad\quad\quad(1)$

　　其中，$\bar{P}=\bar{D}^{-1 / 2} \bar{A} \bar{D}^{-1 / 2}$ 。

　　总之，GCNII

• • 将平滑表示 $\mathbf{P} \mathbf{H}^{l}$ 与到第一层 $\mathbf{H}^{(0)}$ 的初始残差连接相结合；
  • 将 $\mathbf{I}_{n}$ 添加到第 $l$ 个权重矩阵 。通过使用与初始表示 $\mathbf{H}^{0}$ 的连接，GCNII确保每个节点的最终表示至少从输入层保留 $\alpha_{l}$ 倍；

　　GCNII 建立在 Hardt&Ma（2016）的基础上，他证明了 $\mathbf{H}^{l+1}=\mathbf{H}^{l}\left(\mathbf{W}^{l}+\mathbf{I}_{n}\right)$ 形式的恒等映射满足以下性质：1)最优权值矩阵 $\mathbf{W}^{l}$ 具有较小的范数；2)唯一的临界点是全局最小值。第一个特性允许我们在Wl上进行强正则化，以避免过拟合，而后者在训练数据有限的半监督任务中是可取的。第一个特性允许我们在 $\mathbf{W}^{l}$ 上进行正则化，以避免过拟合，而后者在训练数据有限的半监督任务中是可取的。

　　Oono&Suzuki（2019）从理论上证明了GCN层的收敛速度依赖于 $s^{K}$，其中 $s$ 是权重矩阵 $\mathbf{W}^{l}$ 的最大奇异值。GCNII 用 $\left(1-\beta_{l}\right) \mathbf{I}_{n}+\beta_{l} \mathbf{W}^{l}$ 替换 $\mathbf{W}^{l}$ ，导致$\left(1-\beta_{l}\right) \mathbf{I}_{n}+\beta_{l} \mathbf{W}^{l}$ 中的奇异值接近 $1$，这意味着 $s^{K}$ 较大，信息损失减轻。

　　然而，由于GCNII通过均匀平均结合了邻居嵌入，其异质性性能相对较差。另外，对邻近区域的选择性聚合允许关注相关节点。

2.2 Attention Mechanism

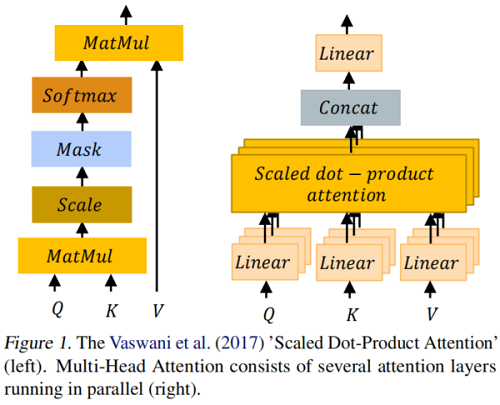
　　注意，本质上是将一个 query Q 和一组 key-value pairs K、V 映射到一个输出，其中 query, keys, values 和输出都是向量（Figure 1）。

　　 

2.3 GAT

　　GCN 将所有邻居赋予相同的权重，而GAT 对不同的邻居赋予不同的权重：

　　　　$H^{l+1}=\sigma( \mathbf{A} \mathbf{h}^{l} \mathbf{W}^{l})  \quad\quad\quad\quad(4)$
　　　　$H^{l+1}=\sigma( \sum_{\mathbf{j} \in \mathcal{N}_{\mathbf{i}}} \mathbf{a}_{i, j}^{l} \mathbf{h}_{j}^{l} \mathbf{W}^{l})  \quad\quad\quad\quad(5)$

　　具体来说，一个评分函数 $e: R^{d} \times R^{d} \rightarrow R$ 计算每条边的得分 $(j，i)$，这表明了邻居 $j$ 的特征对节点 $i$ 的重要性：

　　　　$e\left(\mathbf{h}_{i}, \mathbf{h}_{j}\right)=\operatorname{LeakyReLU}\left(\mathbf{a}^{T} \cdot\left[\mathbf{W} \mathbf{h}_{i} \| \mathbf{W h}_{j}\right]\right) \quad\quad\quad\quad(6)$

　　使用 softmax 对所有邻居 $j \in \mathcal{N}_{i}$ 的注意得分进行归一化，注意函数定义为：

　　　　$\begin{aligned}\alpha_{i j} =\operatorname{softmax}\left(e\left(\mathbf{h}_{i}, \mathbf{h}_{j}\right)\right) =\frac{\exp \left(e\left(\mathbf{h}_{i}, \mathbf{h}_{j}\right)\right)}{\sum \limits_{j^{\prime} \in \mathcal{N}_{i}} \exp \left(e\left(\mathbf{h}_{i}, \mathbf{h}_{j^{\prime}}\right)\right)}\end{aligned} \quad\quad\quad\quad(7)$

　　最后，GAT计算相邻节点的变换特征的加权平均值作为 $i$ 的新表示，使用归一化注意系数：

　　　　$\mathbf{h}_{i}^{\prime}=\sigma\left(\sum \limits_{j \in \mathcal{N}_{i}} \alpha_{i j} \mathbf{W h}_{j}\right)  \quad\quad\quad\quad(8)$

2.4 Dynamic attention

　　Brody等人（2021）指出，标准 GAT 评分函数 $\text{Eq.6}$ 的主要问题是学习到的层 $W$ 和 $a$ 连续应用，因此可以分解成单一的线性层。

　　GATv2 用一个通用逼近器函数代替了线性逼近器。

　　　　$e\left(\mathbf{h}_{i}, \mathbf{h}_{j}\right)=\mathbf{a}^{T} \cdot \text { LeakyReLU }\left(\mathbf{W}\left[\mathbf{h}_{i} \| \mathbf{h}_{j}\right]\right) \quad\quad\quad\quad(9)$

　　因此，GATv2已被证明在有噪声的数据上表现得更好。

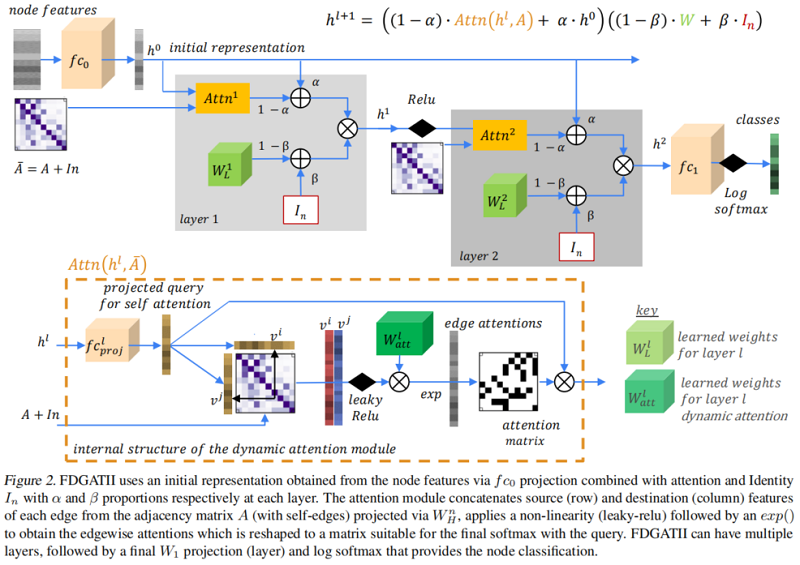
3 Method

　　本质上，我们将GATv2（$\text{Eq.9}$）与初始残差连接和恒等映射结合起来（如 $\text{Eq.3}$），以增强局部聚合，同时确保对异质性的鲁棒性。在 $\text{Eq.3}$ 中，$\alpha$ 和 $\beta$ 分别为初始残差的权值和恒等式的权重。

　　在 $\text{Eq.3}$，GCNII 还使用了一个变量，GCNII*与不同的权重矩阵来平滑表示 $\bar{P} \mathbf{H}^{l}$ 和初始残差 $\mathbf{H}^{0}$。形式上，GCNII*的第 $(l+1)$ 层定义为：
　　　　$\begin{array}{r}\mathbf{H}^{l+1}=\sigma\left(\left(1-\alpha_{l}\right) \overline{\mathbf{P}} \mathbf{H}^{l}\left(\left(1-\beta_{l}\right) \mathbf{I}_{n}+\beta_{l} \mathbf{W}_{1}^{l}\right)\right. \\\left.+\alpha_{l} \mathbf{H}^{0}\left(\left(1-\beta_{l}\right) \mathbf{I}_{n}+\beta_{l} \mathbf{W}_{2}^{l}\right)\right)\end{array}\quad\quad\quad\quad(10)$

　　在我们的模型中，我们使用了这两种形式的补充方法（$\text{Eq.3}$，$\text{Eq.10}$）。

　　框架如下：

　　 

3 Experiment

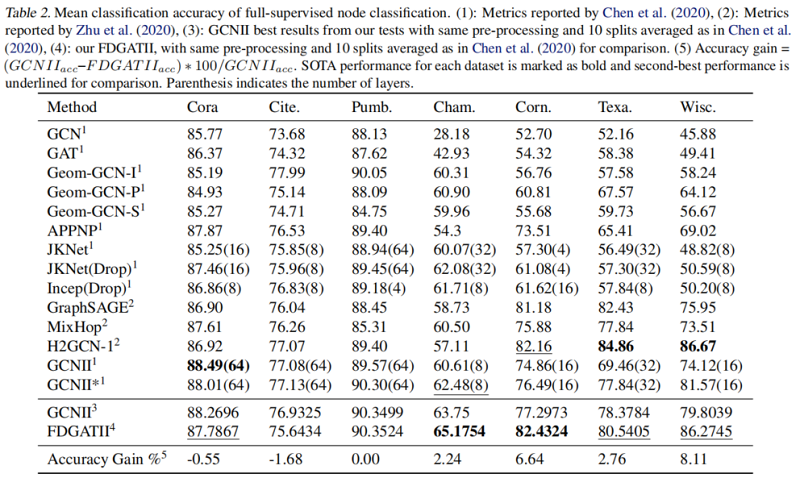
全监督节点分类