论文信息
论文标题:SCGC : Self-Supervised Contrastive Graph Clustering
论文作者:Gayan K. Kulatilleke, Marius Portmann, Shekhar S. Chandra
论文来源:2022, arXiv
论文地址:download
论文代码:download
1 Introduction
目前 GAE 存在的问题
-
- over-smoothing
- noisy neighbours (heterophily)
- the suspended animation problem
创新点:
-
- 使用 MLP 作为 backbone,简单、高效;
- 为加入结构信息,使用 结构损失 作为目标函数;
模型:Graph-MLP 改版
2 Method
整体框架如 Figure 1 所示:
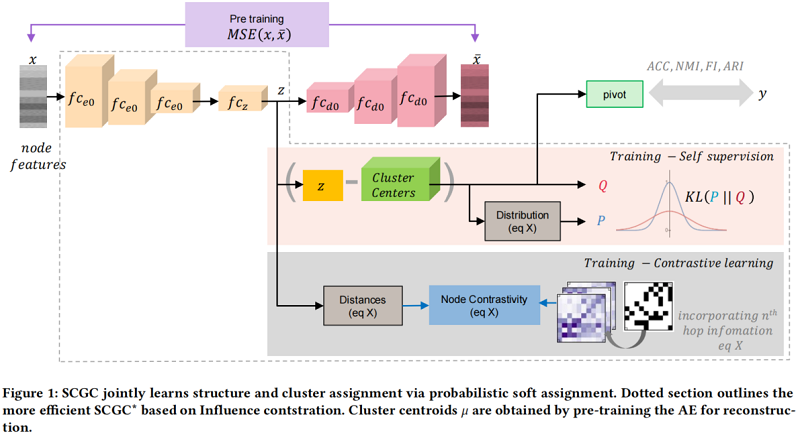
2.1 Graph structure by contrastive loss
对比损失使正或连通节点更近,负或不连通节点在特征空间中更远。基于此思想,将拓扑结构信息合并到嵌入中。
2.1.1 Influence Augmented Contrastive (IAC) loss.
考虑不同深度的节点之间的影响,本文考虑 可加性,对于一个给定的 深度,总影响定义为:
其中, 为深度 处节点 之间关系的系数。
给定 ,将 节点的 损失表示为:
其中, 为温度参数, 为节点 与 之间连接的影响。
对于每个节点, 邻域内的节点被认为是正样本,将其与所有节点进行对比。 损失鼓励有影响的节点在嵌入空间中比无影响的节点更近。接下来,概述了如何计算累积影响。
2.1.2 Determining Influence
归一化邻接矩阵:
次幂提供了节点 和 之间的 跳关系的强度。
通过计算节点之间的累加关系作为节点关系强度,而不是限制在任意的第 跳邻域上。即,将归一化邻接矩阵的 次累积幂定义为 ,其中,。 包含了 中所有先前的邻域跳跃关系的聚合集。 只需要在训练之前计算一次,开销很少。另外,当节点 对节点 的 邻居产生非零影响时, 才能得到非零值。
与我们在影响方面的工作不同,Graph-MLP 提出了基于余弦相似度的 NContrast (NC) 损失进行分类,其中每个节点只考虑 邻域,而不考虑更全面的加性影响。其 的计算如下:
或 的对比损失定义为:
2.2 Self supervised clustering
图聚类本质上是一项无监督的任务,没有反馈来指导优化过程。为此,使用概率分布导出的软标签作为聚类增强的自监督机制,有效地将聚类叠加到嵌入上。
首先获得软集群分配概率 ,嵌入 和簇中心 ,使用 student's t -distribution 作为内核来衡量嵌入和质心之间的相似性,为处理不同的簇:
其中,簇中心 由预先训练过的 AE 的嵌入上的 经 初始化, 是 Student's t-distribution 的自由度。使用 作为所有样本的聚类分配的分布,并在实验中设置 。
节点在 中具有更高的软分配概率,通过将 提高到二次幂并进行归一化,定义一个强调高置信度分配的目标分布,将其定义为:
其中, 为质心 的软簇频率。
为了使数据表示更接近聚类中心,将 KL 散度损失用于 和 分布最小化,迫使当前分布 接近高置信度的目标分布 。通过使用分布 来实现目标分布 来自监督簇分配,然后通过最小化 KL 散度来依次监督分布 ,如下:
2.3 Initial centroids and embeddings
为了提取节点特征并获得初始嵌入 和聚类质心 进行优化,我们采用了基于AE的预训练阶段。首先,我们使用编码器-解码器通过最小化原始数据 和重建数据 重构损失来提取潜在嵌入 ,即:
2.4 Final proposed models
3 Experiments
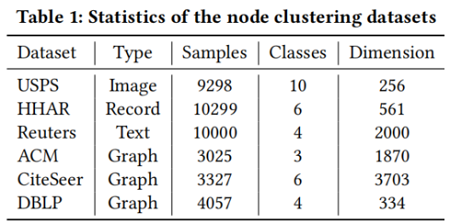
数据集
聚类性能

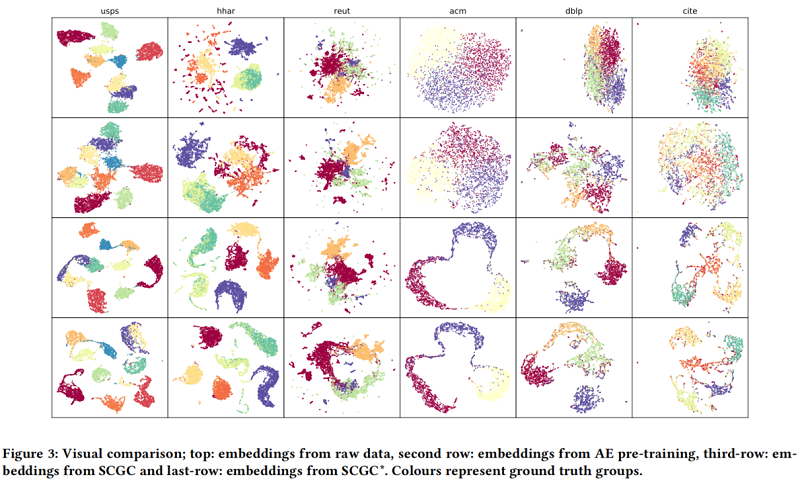
定性结果
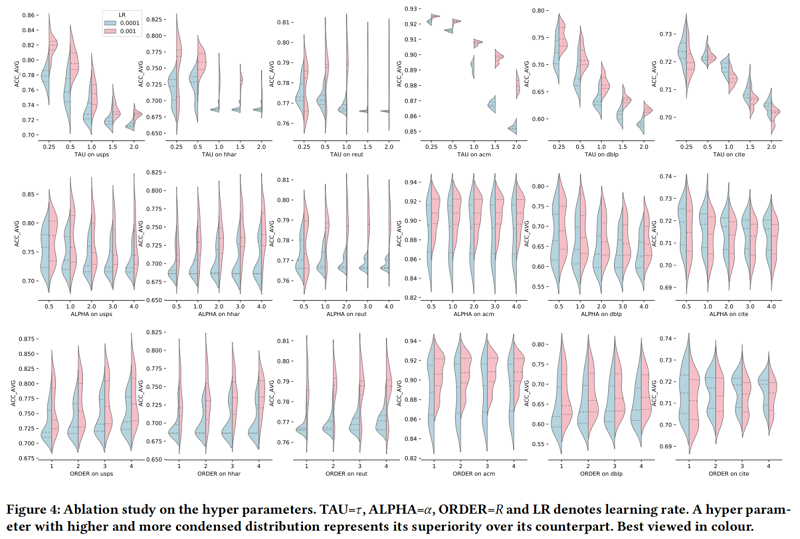
消融实验
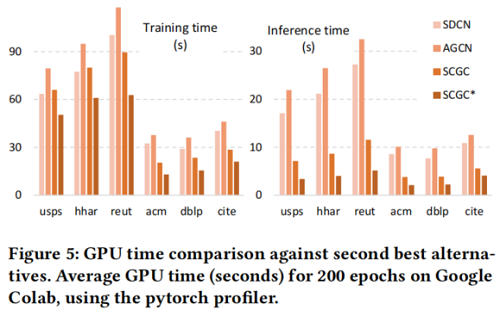
时间开销
4 Conclusion
使用 MLP 作为编码器,并采用结构对比损失做指导。
修改历史
2022-05-20 创建文章
2022-06-23 二次修改
因上求缘,果上努力~~~~ 作者:别关注我了,私信我吧,转载请注明原文链接:https://www.cnblogs.com/BlairGrowing/p/16290017.html



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· winform 绘制太阳,地球,月球 运作规律
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 上周热点回顾(3.3-3.9)
· 超详细:普通电脑也行Windows部署deepseek R1训练数据并当服务器共享给他人