Blair

论文信息

论文标题：Bilinear Graph Neural Network with Neighbor Interactions
论文作者：Hongmin Zhu, Fuli Feng, Xiangnan He, Xiang Wang, Yan Li, Kai Zheng, Yongdong Zhang
论文来源：2019, NeurIPS
论文地址：download 
论文代码：download 

1 Introduction

　　GNNs 中的图卷积操作可以认为是对目标节点的邻居特征线性聚合（加权和）。虽然它改进了目标节点的表示，但这种线性聚合假设邻居节点是相互独立的，而忽略了它们之间可能存在的相互作用。

　　

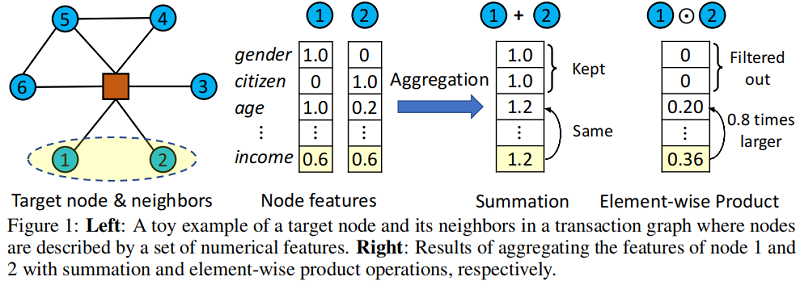
　　在某些情况下，相邻节点之间的相互作用可能是一个指示目标节点特征的强信号。Figure 1 (left) 展示了交易图中目标节点及其邻居的一个玩具示例，其中边表示货币转移关系，节点由一组诸如年龄和收入等特征来描述。考虑评估目标节点的信用等级，直觉是，与富有朋友有密切业务关系的客户有更高的机会偿还贷款。

　　在 Figure 1 (right) 中，我们展示了基于$\text{ sum}$ 的线性聚合器——现有 GNNs 中的一种常见选择——未能突出 $\text{income}$ 特征。相比之下，通过使用基于乘法捕获节点交互的 $\text{Product}$ 聚合器，共享高收入的潜在信号被突出显示，作为辅助效应，一些不太有用的特性被归零。

　　GNNs 中的图卷积操作一般满足两个条件：

• • permutation invariant
  • linear complexity

2 Method

2.1 Preliminaries

　　定义：

• • 图 $G=\left(\mathbf{A} \in\{0,1\}^{N \times N}, \mathbf{X} \in \mathbb{R}^{N \times F}\right)$；
  • 节点 $v$ 的邻居 $\tilde{\mathcal{N}}(v)=\{v\} \cup \mathcal{N}(v)$；
  • 加上自环的节点 $v$ 的邻居 $\tilde{\mathcal{N}}(v)=\{v\} \cup \mathcal{N}(v)$；
  • 节点 $v$ 的度(带自环) $\tilde{d}_{v}=|\tilde{\mathcal{N}}(v)|=d_{v}+1$；
  • 节点 $v$ 的表示 $\mathbf{h}_{v} \in \mathbb{R}^{D}$ ；

　　spatial GNN （GAT）通过递归地聚合来自邻居的特征来实现这一目标：

　　　　$\mathbf{h}_{v}^{(k)}=A G G\left(\left\{\mathbf{h}_{i}^{(k-1)}\right\}_{i \in \tilde{\mathcal{N}}(v)}\right)=\sum\limits _{i \in \tilde{\mathcal{N}}(v)} a_{v i} \mathbf{h}_{i}^{(k-1)} \mathbf{W}^{(k)} \quad\quad\quad(1)$

　　AGG 函数通常被实现为一个加权和，其中 $a_{vi}$ 为邻域 $i$ 的权重。在 GCN 中，$a_{v i}$ 被定义为 $1 / \sqrt{\tilde{d}_{v} \tilde{d}_{i}}$，这是基于拉普拉斯理论的。然而，这种加权和的一个限制是，没有邻居表示之间的交互作用被建模。虽然使用更强大的特征转换函数，如多层感知器(MLP)可以缓解这个问题，但这个过程是相当隐含的和无效的。来自[2]的经验证据，表明MLP在捕获输入特征之间的乘法关系方面效率低下。在这项工作中，我们建议显式地将基于乘法的节点交互注入到AGG函数中。

2.2 Bilinear Aggregator

　　我们提出了一种适用于局部结构中邻居相互作用建模的双线性聚合器：

　　　　${\large B A\left(\left\{\mathbf{h}_{i}\right\}_{i \in \tilde{N}(v)}\right)=\frac{1}{b_{v}} \sum\limits _{i \in \tilde{\mathcal{N}}(v)} \sum\limits _{j \in \tilde{\mathcal{N}}(v) \& i<j} \mathbf{h}_{i} \mathbf{W} \odot \mathbf{h}_{j} \mathbf{W} }   \quad\quad\quad(2)$

　　其中：

• • $\odot$ 为哈达玛积；
  • $v$ 目标节点；
  • $i$ 和 $j$ 是扩展邻居 $\tilde{\mathcal{N}}(v)$ 的节点索引；
  • $b_{v}=\frac{1}{2} \tilde{d}_{v}\left(\tilde{d}_{v}-1\right)$ 表示目标节点 $v$ 的交互次数，对得到的表示进行归一化，以消除节点度的偏差；

　　值得注意的是，我们考虑了目标节点本身，并聚合了来自扩展邻居的信息，这些信息虽然看起来与GNN相同，但原因不同。在GNN中，考虑目标节点是在分层聚合过程中保留其信息，而在BGNN 中，我们考虑的是目标节点与其邻居之间的相互作用也可能携带有用的信号。例如，对于只有一个邻居的稀疏节点，邻居之间的交互不存在，而目标节点和邻居节点之间的交互可能特别有用。

Time Complexity Analysis

　　乍一看，双线性聚合器考虑了邻居（包括目标节点）之间的所有成对交互，因此可能具有二次时间复杂度，高于加权和。然而，通过类似于FM中使用的数学重新公式，我们可以在线性时间内计算聚合器 $\mathcal{O}(|\tilde{\mathcal{N}}(v)|)$，这与与加权和相同。为了证明这一点，我们将 $\text{Eq.2}$ 的等价形式重写为：

　　　　${\large \begin{array}{l} B A\left(\left\{\mathbf{h}_{i}\right\}_{i \in \tilde{\mathcal{N}}(v)}\right)&=\frac{1}{2 b_{v}}\left(\sum\limits _{i \in \tilde{\mathcal{N}}(v)} \sum\limits _{j \in \tilde{\mathcal{N}}(v)} \mathbf{s}_{i} \odot \mathbf{s}_{j}\right.\left.-\sum\limits _{i \in \tilde{\mathcal{N}}(v)} \mathbf{s}_{i} \odot \mathbf{s}_{i}\right)\\  &=\frac{1}{2 b_{v}}((\underbrace{\sum\limits _{i \in \tilde{\mathcal{N}}(v)} \mathbf{s}_{i}}_{\mathcal{O}(|\tilde{\mathcal{N}}(v)|)})^{2}-\underbrace{\sum\limits _{i \in \tilde{\mathcal{N}}(v)} \mathbf{s}_{i}^{2}}_{\mathcal{O}(|\tilde{\mathcal{N}}(v)|)} )\end{array}}    \quad\quad\quad(3)$

　　其中，$\mathbf{s}_{i}=\mathbf{h}_{i} \mathbf{W} \in \mathbb{R}^{D}$

　　可以看出，通过数学的重新表述，我们可以将成对元素级积的和减少为两项的负值，其中每一项都是邻域表示（或其平方）的加权和，可以在 $\mathcal{O}(|\tilde{\mathcal{N}}(v)|)$ 时间内计算。注意，权值矩阵 $W$ 是聚合器中的一个标准操作，因此为了简洁起见，省略了它的时间代价。

Proof of Permutation Invariant

　　从简化的 $\text{Eq.3}$ 可以直观地理解这个特性：当改变输入向量的顺序时，输入的和（第一项）和输入的平方和（第二项）不会改变。因此，输出保持不变，并满足排列不变性。为了提供一个严格的证明，我们给出了双线性聚合器的矩阵形式，这也促进了BGNN的矩阵级实现。双线性聚合器的矩阵形式为：

　　　　$B A(\mathbf{H}, \mathbf{A})=\frac{1}{2} \mathbf{B}^{-1}\left((\tilde{\mathbf{A}} \mathbf{H W})^{2}-\tilde{\mathbf{A}}(\mathbf{H W})^{2}\right)    \quad\quad\quad(4)$

　　其中，

• • $\mathbf{H} \in \mathbb{R}^{N \times D}$ 存储所有节点的表示向量 $h$；
  • $\tilde{\mathbf{A}}=\mathbf{A}+\mathbf{I}$ 是图的邻接矩阵；
  • $\mathbf{I} \in \mathbb{R}^{N \times N}$ 是一个单位矩阵；
  • $B$ 是一个对角矩阵，且 $B_{v v}=b_{v}$；
  • $(\cdot)^{2}$ 表示两个矩阵的逐元素乘法；

　　设 $\mathbf{P} \in \mathbb{R}^{N \times N}$ 是置换矩阵（permutation matrix） 满足：

• • $\mathbf{P}^{T} \mathbf{P}=\mathbf{I}$
  • 对于任何矩阵 $\mathbf{M}$，如果 $\mathbf{P M}$ 存在，则满足 $\mathbf{P M} \odot \mathbf{P M}=\mathbf{P}(\mathbf{M} \odot \mathbf{M})$ 。

　　当我们在节点上应用排列 $\mathbf{P}$ 时，$\mathbf{H}$ 变为 $\mathbf{P H}$，$\tilde{\mathbf{A}}$ 变为 $\mathbf{P} \tilde{\mathbf{A}} \mathbf{P}^{T}$，$\mathbf{B}$ 变为 $\mathbf{P B} \mathbf{P}^{T}$，这导致：

　　　　$\begin{array}{l}B A\left(\mathbf{P H}, \mathbf{P A} \mathbf{P}^{T}\right)&=\frac{1}{2} \mathbf{P B}^{-1} \mathbf{P}^{T}\left(\mathbf{P}(\tilde{\mathbf{A}} \mathbf{H W})^{2}-\mathbf{P } \tilde{\mathbf{A}}(\mathbf{H W})^{2}\right) \\&=\frac{1}{2} \mathbf{P B}{ }^{-1} \mathbf{P}^{T} \mathbf{P}\left((\tilde{\mathbf{A}} \mathbf{H W})^{2}-\tilde{\mathbf{A}}(\mathbf{H W})^{2}\right)\\&=\mathbf{P} \cdot B A(\mathbf{H}, \mathbf{A})\end{array}$

　　上述说明了它表示了排列不变性。

2.3 BGNN Model

　　我们现在来描述所提出的BGNN模型。由于双线性聚合器强调节点交互，并使用加权和聚合器对不同的信号进行编码，我们将它们结合起来，构建一个更具表现性的图卷积网络。我们采用了一个简单的线性组合方案，定义了一个新的图卷积算子为：

　　　　$\begin{aligned}\mathbf{H}^{(k)} &=B G N N\left(\mathbf{H}^{(k-1)}, \mathbf{A}\right) \\&=(1-\alpha) \cdot A G G\left(\mathbf{H}^{(k-1)}, \mathbf{A}\right)+\alpha \cdot B A\left(\mathbf{H}^{(k-1)}, \mathbf{A}\right)\end{aligned}   \quad\quad\quad(5)$

　　Figure 2 说明了模型框架。

　　 

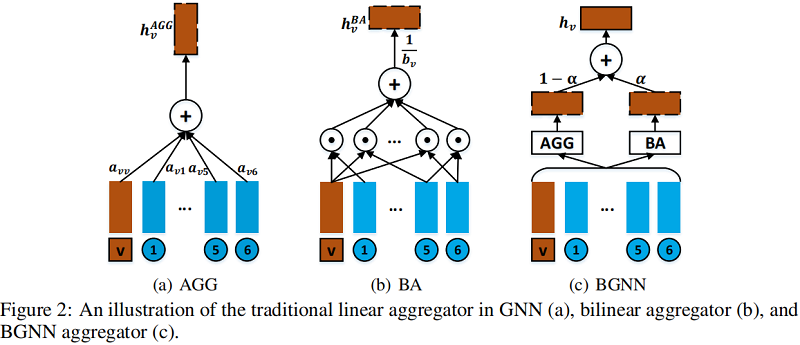
　　由于 AGG 和 BA 都是置换不变的，所以发现这个图卷积算子也是置换不变的是平凡的。当 $\alpha$ 设置为 $0$ 时，不考虑节点交互，BGNN降级为GNN；当 $\alpha$ 设置为 $1$ 时，BGNN只使用双线性聚合器来处理来自邻居的信息。我们的实证研究表明，在 $0$ 和 $1$ 之间的中间值通常可以导致更好的性能，验证了建模节点交互的有效性，并且最优设置在不同的数据集上有所不同。

2.4 Multi-layer BGNN

　　传统的GNN模型通过堆叠多个聚合器，以递归的方式对来自多跳邻居的信息进行编码。例如，$2$ 层的 GNN 模型被形式化为：

　　　　$G N N_{2}(\mathbf{X}, \mathbf{A})=\underbrace{A G G}_{\text {2nd layer }}(\sigma(\underbrace{A G G}_{1 \text { st layer }}(\mathbf{X}, \mathbf{A})), \mathbf{A})  \quad\quad\quad(6)$

　　其中 $\sigma$ 是一个非线性激活函数。类似地，我们也可以以相同的递归方式设计一个 $2$ 层的 BGNN 模型：

　　　　$\underbrace{B G N N}_{\text {2nd layer }}(\sigma(\underbrace{B G N N}_{1 \text { st layer }}(\mathbf{X}, \mathbf{A})), \mathbf{A})     \quad\quad\quad(7)$

　　然而，这种直接的多层扩展涉及到意外的高阶交互。在两层的情况下，第二层的表示将包括两跳邻居之间的部分四阶交互作用，这是难以解释和不合理的。当将BGNN扩展到多层，即 $K$ 层时，我们仍然希望捕获成对的交互，但在 $K$ 跳邻居之间。为此，我们不是直接叠加BGNN层，而是将 $2$ 层BGNN模型定义为：

　　　　$\begin{aligned}B G N N_{2}(\mathbf{X}, \mathbf{A}) &=(1-\alpha) \cdot G N N_{2}(\mathbf{X}, \mathbf{A}) \\&+\alpha\left[(1-\beta) \cdot B A(\mathbf{X}, \mathbf{A})+\beta \cdot B A\left(\mathbf{X}, \mathbf{A}^{(2)}\right)\right]\end{aligned}      \quad\quad\quad(8)$

　　其中，$\mathbf{A}^{(2)}=  binarize  (\mathbf{A} \mathbf{A})$ 存储了图的 $2$ 跳连接性。$binarize$ 将非零条目转换为 $1$。因此，$\mathbf{A}^{(2)}$ 中的非零条目 $(v, i)$ 意味着节点 $v$ 可以在两跳内到达节点 $i$。$\beta$ 是一个超参数，可以权衡 $1$ 跳邻居和 $2$ 跳邻居之间的双线性相互作用的强度。

　　按照同样的原理，我们将BGNN层BGNN定义为：
　　　　$\begin{array}{l}B G N N_{K}(\mathbf{X}, \mathbf{A})&=(1-\alpha) \cdot G N N_{K}(\mathbf{X}, \mathbf{A}) +\alpha \cdot\left(\sum\limits _{k=1}^{K} \beta_{k} \cdot B A\left(\mathbf{X}, \mathbf{A}^{(k)}\right)\right) \\\text { s.t. }, \sum\limits _{k=1}^{K} \beta_{k}&=1\end{array}   \quad\quad\quad(9)$

　　$\mathbf{A}^{(k)}=  binarize  (\underbrace{\mathbf{A} \cdots \mathbf{A}}_{k \text { times }})$ 表示 $k$ 跳连接性的邻接矩阵，$G N N_{K}$ 表示可以递归定义的正常 $k$ 层 GNN。$k$ 层 BGNN 的时间复杂度由 $\mathbf{A}^{(K)}$ 中非零条目的数量决定。为了降低实际的复杂性，我们可以遵循 GraphSage 中的采样策略，采样部分高跳邻居，而不是使用所有的邻居。

Model Training

　　BGNN是一个可微分模型，因此它可以对具有梯度下降的任何差分损失进行端到端优化。在这项工作中，我们关注半监督节点分类任务，在标记节点上使用交叉熵损失优化BGNN(与GCN工作相同的设置，以进行公平的比较)。由于实验数据不大，我们以矩阵形式实现了层图卷积，将可以扩展到大图的批实现和邻居采样作为未来的工作。

3 Experiments

数据集

　　每个节点都有一个具有文档类别的一个 one-hot 的标签。我们在以前的工作中使用了相同的数据分割。也就是说，每个类使用 20 个有标记的节点用于训练。使用 500 个节点和 1000个节点分别作为验证集和测试集。请注意，训练进程可以使用所有节点的特性。对于这个数据分割，我们报告了超过 10 个不同的随机初始化的平均测试精度。

半监督节点分类

　　

　　

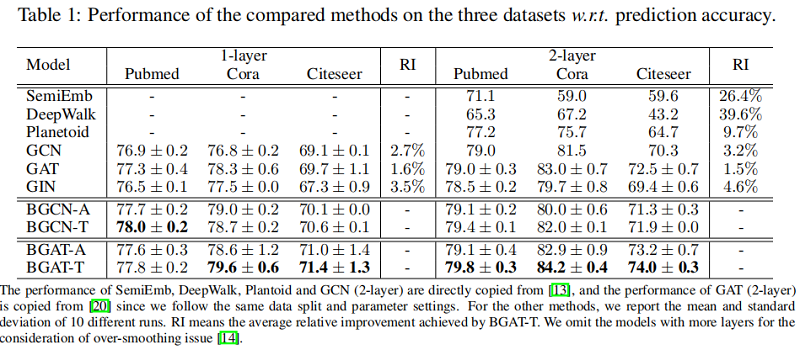
4 Conclusion

　　在本文中，我们提出了一种新的图神经网络框架BGNN，它通过考虑邻居节点之间的相互作用来增强普通GNN的表达性。邻居节点的交互被一个简单但精心设计的双线性聚合器捕获。双线性聚合器的简单性使得BGNN具有与普通GNNw.r.t.相同的模型复杂度可学习参数的数量和分析的时间复杂度。此外，证明了双线性聚合器是置换不变的，这是GNN聚合器[9,27]的一个重要性质。我们将所提出的BGNN应用于半监督节点分类任务，在三个基准数据集上取得了最先进的性能。