论文解读（ClusterSCL）《ClusterSCL: Cluster-Aware Supervised Contrastive Learning on Graphs》

论文信息

论文标题：ClusterSCL: Cluster-Aware Supervised Contrastive Learning on Graphs
论文作者：Yanling Wang, Jing Zhang, Haoyang Li, Yuxiao Dong, Hongzhi Yin, Cuiping Li
论文来源：2022, WWW
论文地址：download 
论文代码：download

1 Introduction

　　图上的监督对比学习很难处理拥有较大的类内（intra-class）差异，类间（inter-class）相似性的数据集。

　　 

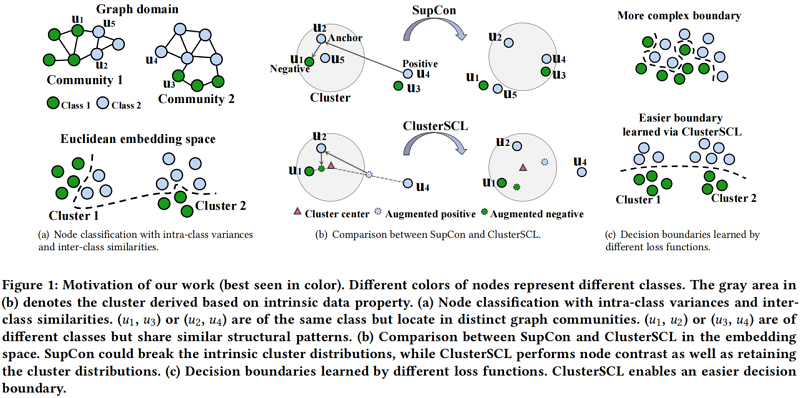
　　Figure 1(a) 顶部中 $(u_1,u_3)$ 、$(u_2,u_4)$ 属于同一个类，但在不同的图社区(类内差异，intra-class variances)，而 $(u_1,u_2)$、$(u_3,u_4)$ 来自不同的类但在同一图社区（类间相似性，inter-class similarities）。针对上述问题，需要找出一个复杂的决策边界，见 Figure 1(a) 底部。

　　当执行自监督对比（SupCon）为 $u_{2}$ 寻找锚节点，如 Figure 1(b) 所示，正样本对属于同一类但位于不同的簇，如 $\left(u_{2}, u_{4}\right)$。简单地把正对（相同标签节点）放在同一嵌入空间，可能间接把不同类的节点，如 $\left(u_{2}, u_{3}\right)$ 看成正对，因为 $u_{3}$ 和 $u_{4}$ 社区结构类似。同时，对属于不同类但位于同一簇中的负样本对，如 $\left(u_{2}, u_{1}\right)$，简单地把它们推开可能间接推开同一类的节点，如 $\left(u_{2}, u_{5}\right)$，因为 $u_{5}$ 在结构上与 $u_{1}$ 相似。

　　上述问题总结为：简单的执行类内差异小，类间方差大的思想，可能会造成分类错误，导致 Figure 1(c) 顶部显示的更复杂的决策边界。

　　本文的想法简单的如 Figure 1(b) 底部所示。

2 Method

2.1 Base CL Scheme: SupCon

　　对一个 batch 内的节点 $v_{i}$ ，其正样本下标集合 $S_{i}$，$s_{i} \in S_{i}$ 是 $v_{i}$ 正样本的索引。SupCon 损失函数如下：

　　　　${\large \mathcal{L}_{\text {SupCon }}=-\sum\limits _{v_{i} \in B} \frac{1}{\left|S_{i}\right|} \sum\limits _{s_{i} \in S_{i}} \log \frac{\exp \left(\mathbf{h}_{i}^{\top} \mathbf{h}_{s_{i}} / \tau\right)}{\sum\limits _{v_{j} \in B \backslash\left\{v_{i}\right\}} \exp \left(\mathbf{h}_{i}^{\top} \mathbf{h}_{j} / \tau\right)}}  \quad\quad\quad(3)$

　　其中 $\mathbf{h}$ 代表着经 $\ell_{2}$-normalized 处理后的表示。

2.2 Proposed CL Scheme: ClusterSCL

　　假设有 $M$ 个簇，引入潜在变量 $c_{i} \in\{1,2, \ldots, M\}$ 来指示节点 $v_{i}$ 归于哪个簇。给定一个锚节点 $v_{i}$ 和一个节点 $v_{j}$，$\text{CDA}$ 通过以下线性插值构造一个 $v_{j}$ 的加强版本：

　　　　$\tilde{\mathbf{h}}_{j}=\alpha \mathbf{h}_{j}+(1-\alpha) \mathbf{w}_{c_{i}} \quad\quad\quad(4)$

　　其中，$\mathbf{w}=\left\{\mathbf{w}_{m}\right\}_{m=1}^{M}$ 表示簇原型。$\tilde{\mathbf{h}}_{j}$ 包含来自 $v_{j}$ 的信息，以及节点 $v_{i}$ 所属的簇的信息。

　　如果锚节点 $v_{i}$ 和对比样本 $v_{j}$ 本身在嵌入空间已经足够相近，那么可以选择直接对比，也可以为其分配一个更大的 $\alpha$  ，使 $v_{j}$  包含更多自身信息。相反，若 $v_{i}$ 和 $v_{j}$ 在嵌入空间中彼此远离，那么使用较小的 $\alpha$ 来衰减来自 $v_{j}$ 的信息，以保证锚点和增强样本之间不会太远。

　　这种方式缩小了特征空间，并拉近了远正样本对之间的距离和拉远了近负样本对之间的距离，帮助保留节点的聚类分布。$\alpha$ 控制着拉近还是拉远，图解如  Figure 2 所示：

　　

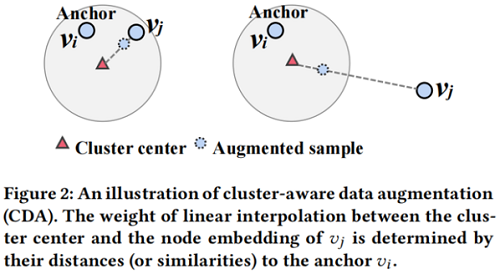
　　本文从从正\负样本对的角度设计了调整 $\alpha$ 的原则，计权重 $\alpha$ 计算方式为：

　　　　${\large \alpha=\frac{\exp \left(\mathbf{h}_{i}^{\top} \mathbf{h}_{j}\right)}{\exp \left(\mathbf{h}_{i}^{\top} \mathbf{h}_{j}\right)+\exp \left(\mathbf{h}_{i}^{\top} \mathbf{w}_{c_{i}}\right)}}  \quad\quad\quad(5)$

　　PS：$\mathbf{h}_{i}$ 和 $\mathbf{h}_{j}$ 位于半径为 $1$ 的超球面的表面上，我们有 $\left\|\mathbf{h}_{i}-\mathbf{h}_{j}\right\|^{2}=2-2 \mathbf{h}_{i}^{\top} \mathbf{h}_{j}$，即表示内积越大代表着表示之间的欧几里得距离小。

　　mixup 和 CDA 都采用线性插值操作来生成虚拟数据点。在这里，阐述 CDA 与 mixup  之间的区别：

• • mixup 通过扩大训练集来提高神经网络的泛化能力，而 CDA 则旨在处理 SupCon 学习中的类内差异和类间相似的问题；　　
  • mixup 在两个样本之间执行线性插值，而 CDA 在一个样本和一个原型之间执行线性插值；　　
  • mixup 独立于学习过程，而 ClusterSCl 中的 CDA 被集成到学习过程中，以利用可学习的参数；

Integrating Clustering and CDA into SupCon Learning

　　流程如下：

　　 

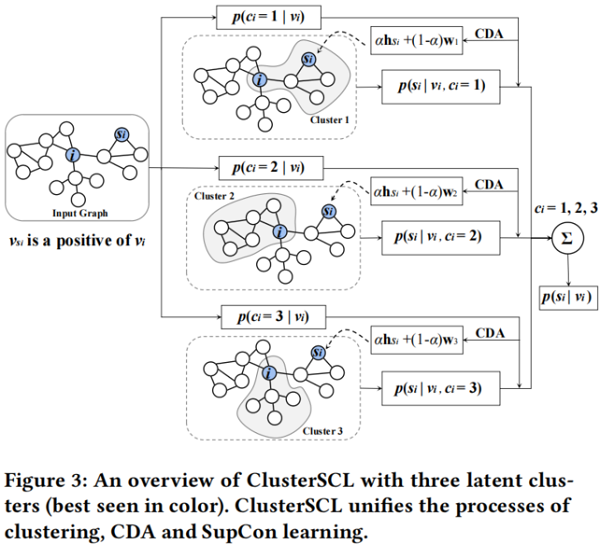
　　在执行 CDA 之前，需要通过下式知道锚节点 $v_i$ 属于哪个簇：

　　　　${\large p\left(c_{i} \mid v_{i}\right)=\frac{\exp \left(\mathbf{h}_{i}^{\top} \mathbf{w}_{c_{i}} / \kappa\right)}{\sum\limits _{m=1}^{M} \exp \left(\mathbf{h}_{i}^{\top} \mathbf{w}_{m} / \kappa\right)}}   \quad\quad\quad(7)$

　　其中，$\kappa$ 为用于调整聚类分布的温度参数，$p\left(c_{i} \mid v_{i}\right) $ 可以视为一个基于原型的软聚类模块。

　　基于 CDA 推导出的节点版本（即已经使用了线性插值），对以下实例识别任务进行建模（聚类感知识别器）：

　　　　${\large \begin{aligned}p\left(s_{i} \mid v_{i}, c_{i}\right) &=\frac{\exp \left(\mathbf{h}_{i}^{\top} \tilde{\mathbf{h}}_{s_{i}} / \tau\right)}{\sum\limits _{v_{j} \in V \backslash\left\{v_{i}\right\}} \exp \left(\mathbf{h}_{i}^{\top} \tilde{\mathbf{h}}_{j} / \tau\right)} \\&=\frac{\exp \left(\mathbf{h}_{i}^{\top}\left(\alpha \mathbf{h}_{s_{i}}+(1-\alpha) \mathbf{w}_{c_{i}}\right) / \tau\right)}{\sum\limits _{v_{j} \in V \backslash\left\{v_{i}\right\}} \exp \left(\mathbf{h}_{i}^{\top}\left(\alpha \mathbf{h}_{j}+(1-\alpha) \mathbf{w}_{c_{i}}\right) / \tau\right)}\end{aligned}}   \quad\quad\quad(6)$

　　由于我们已经对软聚类模块 $p\left(c_{i} \mid v_{i}\right)$ 和聚类感知识别器 $p\left(s_{i} \mid v_{i}, c_{i}\right)$ 进行了建模，因此ClusterSCL  可以建模为以下实例识别任务：

　　　　$p\left(s_{i} \mid v_{i}\right)=\int p\left(c_{i} \mid v_{i}\right) p\left(s_{i} \mid v_{i}, c_{i}\right) d c_{i}   \quad\quad\quad(8)$

Inference and Learning 

　　实际上，由于对数操作内的求和，最大化整个训练数据的对数似然值是不平凡的。我们可以采用 EM 算法来解决这个问题，其中我们需要计算后验分布：

　　　　${\large p\left(c_{i} \mid v_{i}, s_{i}\right)=\frac{p\left(c_{i} \mid v_{i}\right) p\left(s_{i} \mid v_{i}, c_{i}\right)}{\sum\limits _{m=1}^{M} p\left(m \mid v_{i}\right) p\left(s_{i} \mid v_{i}, m\right)} } \quad\quad\quad(9)$

　　然而，由于对整个节点的求和 $\sum\limits _{v_{j} \in V \backslash\left\{v_{i}\right\}} \exp \left(\mathbf{h}_{i}^{\top} \tilde{\mathbf{h}}_{j} / \tau\right)$，计算后验分布是禁止的。我们最大化了由以下方法给出的 $\log p\left(s_{i} \mid v_{i}\right)$ 的 evidence 下界(ELBO)：

　　　　${\large \begin{array}{l}\log p\left(s_{i} \mid v_{i}\right) &\geq \mathcal{L}_{\operatorname{ELBO}}\left(\boldsymbol{\theta}, \mathbf{w} ; v_{i}, s_{i}\right)\\&\begin{aligned}:=& \mathbb{E}_{q\left(c_{i} \mid v_{i}, s_{i}\right)}\left[\log p\left(s_{i} \mid v_{i}, c_{i}\right)\right] -\operatorname{KL}\left(q\left(c_{i} \mid v_{i}, s_{i}\right) \| p\left(c_{i} \mid v_{i}\right)\right)\end{aligned}\\\end{array}}   \quad\quad\quad(10)$

　　其中 $q\left(c_{i} \mid v_{i}, s_{i}\right)$ 是一个近似后 $p\left(c_{i} \mid v_{i}, s_{i}\right)$。ELBO的推导在附录a中提供。在这里，我们将变分分布形式化为：

　　　　${\large q\left(c_{i} \mid v_{i}, s_{i}\right)=\frac{p\left(c_{i} \mid v_{i}\right) \tilde{p}\left(s_{i} \mid v_{i}, c_{i}\right)}{\sum\limits _{m=1}^{M} p\left(m \mid v_{i}\right) \tilde{p}\left(s_{i} \mid v_{i}, m\right)}}  \quad\quad\quad(11)$

　　其中 $\tilde{p}\left(s_{i} \mid v_{i}, c_{i}\right)=\exp \left(\mathbf{h}_{i}^{\top} \tilde{\mathbf{h}}_{s_{i}} / \tau\right) / \sum_{v_{j} \in B \backslash\left\{v_{i}\right\}} \exp \left(\mathbf{h}_{i}^{\top} \tilde{\mathbf{h}}_{j} / \tau\right)$ 在一个批次 $B$ 内计算。请注意，$v_{i}$ 和 $v_{s_{i}}$ 都在该批处理中。此外，我们应用 $\tilde{p}\left(s_{i} \mid v_{i}, c_{i}\right)$ 来估计 $\text{Eq.10}$ 中的 $p\left(s_{i} \mid v_{i}, c_{i}\right)$、并在附录B中作出说明。

　　我们通过一种变分EM算法来优化模型参数，其中我们在 E 步推断 $q\left(c_{i} \mid v_{i}, s_{i}\right)$，然后在 M 步优化ELBO。对一批节点进行采样，我们可以最大化以下目标：

　　　　${\large \mathcal{L}_{\mathrm{ELBO}}(\boldsymbol{\theta}, \mathbf{w} ; B) \approx \frac{1}{|B|} \sum\limits _{v_{i} \in B} \frac{1}{\left|S_{i}\right|} \sum\limits _{s_{i} \in S_{i}} \mathcal{L}_{\operatorname{ELBO}}\left(\boldsymbol{\theta}, \mathbf{w} ; v_{i}, s_{i}\right) }   \quad\quad\quad(12)$

　　我们观察到，只有对集群原型使用随机更新才能得到平凡的解决方案，即大多数实例被分配给同一个集群。为了缓解这一问题，我们在每个训练阶段后应用以下更新：

　　　　${\large \mathbf{w}_{m}=\frac{1}{\left|\bar{V}_{m}\right|} \sum\limits_{v_{i} \in \bar{V}_{m}} \mathbf{h}_{i}, m=1,2, \cdots, M   } \quad\quad\quad(13)$

　　其中，$\bar{V}_{m}$ 表示由 METIS 导出的第 $m$ 个图社区中的节点集。在训练之前，我们根据节点间的互连将整个图 $G$ 划分为 $M$ 个图社区。我们使用社区来粗略地描述集群，并对每个社区中的节点嵌入进行平均，以在每个训练阶段后更新集群原型。请注意，ClusterSCL 采用了 $Eq. 7$，为每个节点推导出一个细化的软集群分布。METIS 输出的硬集群分布仅用于原型更新。此外，我们观察到需要对 $\kappa$ 进行细粒度搜索，这是低效的。根据经验，我们使用一个小的 $\kappa$ 来推导一个相对可靠的聚类预测，并引入一个熵项来平滑预测的聚类分布。通过这样做，我们可以避免在 $\kappa$ 上的细粒度搜索。最后，将 ClusterSCL 损失函数形式化为：

　　　　${\large \mathcal{L}(\boldsymbol{\theta}, \mathbf{w} ; B)=-\mathcal{L}_{\mathrm{ELBO}}(\boldsymbol{\theta}, \mathbf{w} ; B)+\frac{\eta}{|B|} \sum\limits _{v_{i} \in B} \sum\limits _{c_{i}=1}^{M} p\left(c_{i} \mid v_{i}\right) \log p\left(c_{i} \mid v_{i}\right)}    \quad\quad\quad(14)$

　　其中，$\eta \in(0,1]$ 为控制平滑强度的熵项的权值。

　　Algorithm 1 显示了使用Clusterscl进行训练的伪代码。我们在附录C中提供了 ClusterSCL 的复杂性分析。

 　　

3 Experiments

　　实验通过回答以下研究问题来展开：（1）ClusterSCL 如何在节点分类任务上执行？（2）CDA是否生效？（3）ClusterSCL 在不同大小的标记训练数据下表现如何？

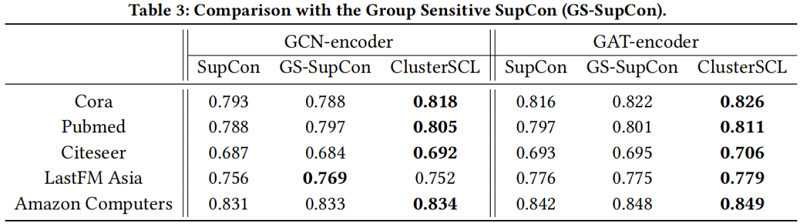
节点分类

　　

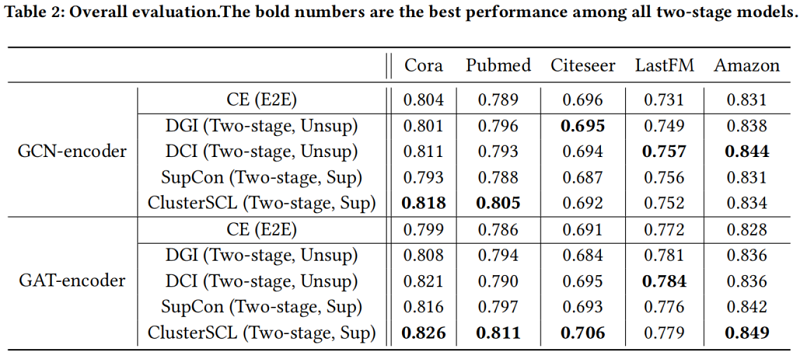
CDA 有效性验证

　　

在不同大小的标记训练数据下的 ClusterSCL 的研究

　　

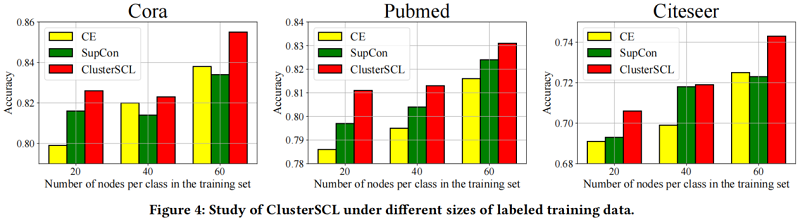
4 Conclusion

　　这项工作初步研究了用于节点分类的图神经网络的监督学习。我们提出了一种简单而有效的对比学习方案，称为聚类感知监督对比学习(聚类scl)。ClusterSCL改进了监督对比(SupCon)学习，并强调了在SupCon学习过程中保留内在图属性的有效性，从而减少了由类内方差和类间相似性引起的负面影响。ClusterSCL比流行的交叉熵、SupCon和其他图对比损失更具有优势。我们认为，ClusterSCL的思想并不局限于图上的节点分类，并可以启发表示学习的研究。