论文解读（DiffPool）《Hierarchical Graph Representation Learning with Differentiable Pooling》

论文信息

论文标题：Hierarchical Graph Representation Learning with Differentiable Pooling
论文作者：Rex Ying, Jiaxuan You, Christopher Morris, Xiang Ren, William L. Hamilton, Jure Leskovec
论文来源：2018, NeurIPS
论文地址：download 
论文代码：download

1 Preamble

　　先针对 Global pooling 痛批一下，即 其忽略了图的层次结构，因为 Global pooling 通常只是简单的使用 求和 或者 神经网络 处理。

　　针对全局池化我见到的一般就是 求和 ，再或者就是 其他池化的组合拼接后再接一个 MLP。

• • $s=\frac{1}{N} \sum\limits_{i=1}^{N} x_{i} $
  • $s=\frac{1}{N} \sum\limits_{i=1}^{N} x_{i} \| \max _{i=1}^{N} x_{i}$

2 Introduction

　　本文提出了 DIFFPOOL，一个可微的图池化模块，可以以分层和端到端的方式适应各种图神经网络架构。

 

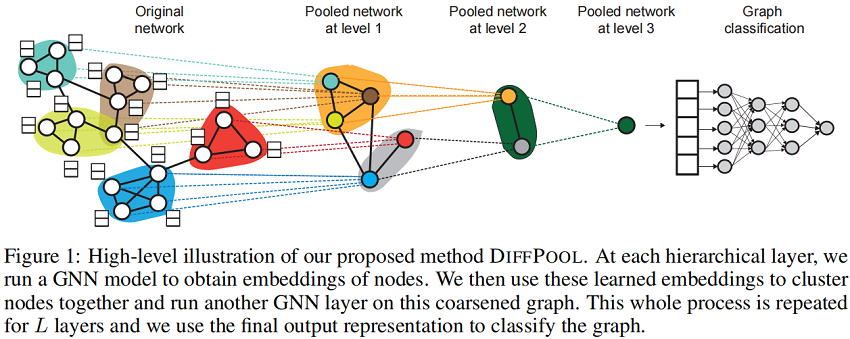
3 Method

3.1  Pooling with an assignment matrix

　　第 $l$ 层的聚类分配矩阵为 $S^{(l)} \in \mathbb{R}^{n_{l} \times n_{l+1}} $。

　　其中：

• • $S^{(l)} $ 的每一行对应第 $l$ 层的 $n_l$ 个节点 ；
  • $S^{(l)}$ 的每一列对应 $l+1$ 层的 $n_{l+1}$ 节点 ；

　　DIFFPOOL  可以表达为 $\left(A^{(l+1)}, X^{(l+1)}\right)=\operatorname{DiFF} \operatorname{POOL}\left(A^{(l)}, Z^{(l)}\right)$ ，即：

　　　　$\begin{array}{l}{\large X^{(l+1)}=S^{(l)^{T}} Z^{(l)} \in \mathbb{R}^{n_{l+1} \times d} } \quad\quad\quad(3) \\{\large A^{(l+1)}=S^{(l)^{T}} A^{(l)} S^{(l)} \in \mathbb{R}^{n_{l+1} \times n_{l+1}}}  \quad\quad\quad(4) \end{array}$

3.2 Learning the assignment matrix

　　嵌入矩阵：

　　　　$Z^{(l)}=\operatorname{GNN}_{l, \text { embed }}\left(A^{(l)}, X^{(l)}\right)   \quad\quad\quad(5)$

 　　分配矩阵：

　　　　$S^{(l)}=\operatorname{softmax}\left(\operatorname{GNN}_{l, \text { pool }}\left(A^{(l)}, X^{(l)}\right)\right)  \quad\quad\quad(6)$

　　Note：最后一层设置聚类分配矩阵设置输出大小为 $1$。

3.3 Auxiliary Link Prediction Objective and Entropy Regularization

　　事实上，$\text{Eq.4}$ 很难通过梯度进行训练，所以本文采用 最小化 

　　　　$L_{\mathrm{LP}}=\left\|A^{(l)}, S^{(l)} S^{(l)^{T}}\right\|_{F}$

　　每个聚类分配矩阵 被希望接近于一个 one-hot 向量，以便明确每个簇的隶属关系，所以本文通过最小化簇分配的熵：

　　　　$L_{\mathrm{E}}=\frac{1}{n} \sum\limits _{i=1}^{n} H\left(S_{i}\right) $

　　其中：

• • $H$ 为熵函数 $H(X)=-\sum \limits_{x\in \mathrm{x}}p(x)\ log p(x)$；
  • $S_{i}$ 为 $S$ 的第 $i$ 行；

　　熵函数如下：

　　

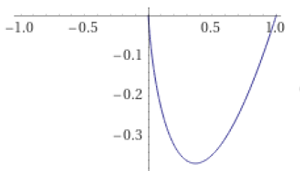
　　在训练过程中，将每层的 $L_{LP} $ 和 $L_{E}$ 添加到分类损失中。

4 Experiments

数据集

　　

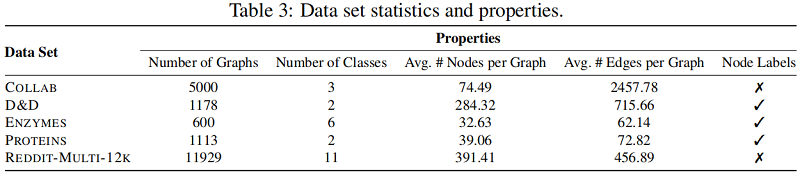
图分类

　　

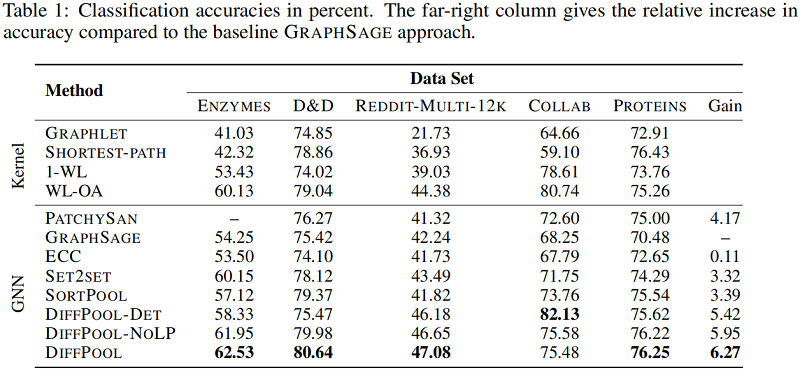
聚类分配分析

　　

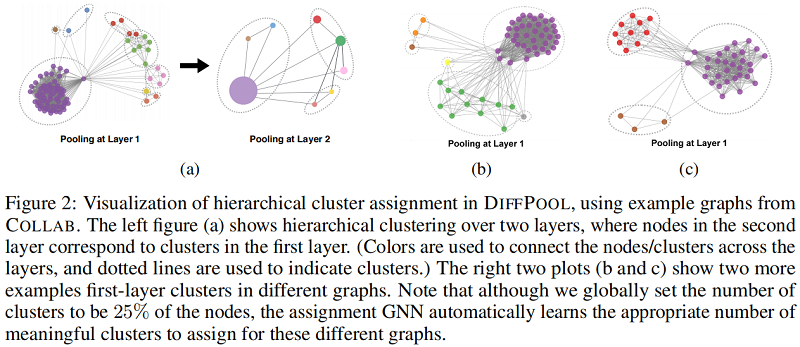
4 Conclusion

　　我们介绍了一种可微池化的gnn方法，它能够提取真实世界图的复杂层次结构。通过将所提出的池化层结合现有的GNN模型，我们在几个图分类基准上获得了新的最先进的结果。有趣的未来发展方向包括学习硬聚类分配，以进一步降低更高层次的计算成本，同时确保可微性，并将分层池化方法应用于其他需要对整个图结构进行建模的下游任务。

修改历史

2022-05-07 创建文章
2022-08-12 修订文章

论文解读目录