论文解读（GMT）《Accurate Learning of Graph Representations with Graph Multiset Pooling》

论文信息

论文标题：Accurate Learning of Graph Representations with Graph Multiset Pooling
论文作者：Jinheon Baek, Minki Kang, Sung Ju Hwang
论文来源：2021, ICLR
论文地址：download 
论文代码：download

1 Introduction

　　图池化存在的问题：获得的图表示需进一步使用池化函数将一组节点表示映射为紧凑的形式。对所有节点表示的简单求和或平均都平等地考虑所有节点特征，而不考虑它们的任务相关性，以及它们之间的任何结构依赖性。

　　图池化方法：

　　 

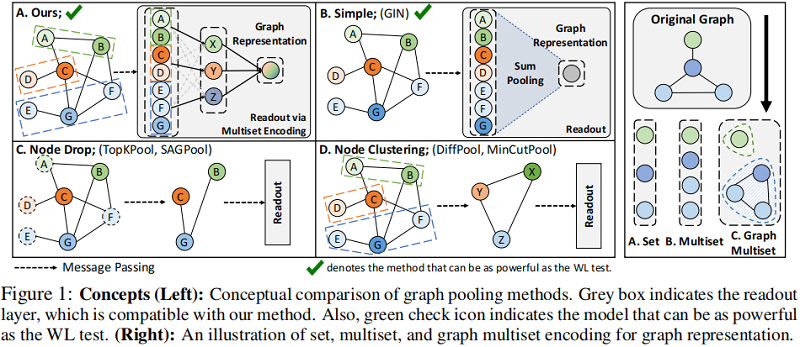
　　图解：

• • Figure 1 (B)：简单对所有节点求和或平均；
  • Figure 1 (C)：节点删除方法，使用来自图卷积层的信息获得每个节点的得分，然后在每个池化步骤中删除得分较低的不必要的节点；
  • Figure 1 (D)：节点聚类方法，利用相似节点的层次结构将相似节点聚类为单个节点；

　　对于节点删除方法存在的问题：在每个池化步骤中都不必要地丢弃一些节点，从而导致那些被丢弃的节点上的信息丢失。

　　对于节点聚类方法存在的问题：计算具有邻接矩阵的密集聚类分配矩阵。这阻止了它们利用图拓扑中的稀疏性，从而导致过高的计算复杂度。

　　我们可以将图表示学习可以看作是一个多集（multiset）编码问题，它允许可能重复的元素，因为一个图可能有冗余的节点表示（见 Figure 1 最右边）。图表示学习可以认为是一个受到结构控制的多集编码问题。编码的目标是：两个不同的图，给出多集的节点特性之间的辅助结构依赖，到两个独特的嵌入。本文利用一个图结构的注意单元来解决这个问题。通过利用这个单元作为一个基本的构建块，我们提出了图多集变换器（Graph Multiset Transformer，GMT），这是一种池化机制，它将给定的图压缩成具有代表性的节点集，然后进一步编码它们之间的关系，以增强图的表示能力。

2 Graph Multiset Pooling

2.1 Preliminaries

　　消息传递的基本定义.....

2.2 Graph Multiset Transformer

Multiset Encoding

　　READOUT  函数需要满足的条件：

• • 单射（injectiveness）
  • 排列不变性（permutation invariance）

Graph Multi-head Attention

　　为克服简单的池化方法（如 sum ）在区分重要节点方面的不足，本文使用注意机制作为池化方案的主要组件。

　　假设有 $n$ 个节点向量，注意力函数的输入(Att)由查询 $\boldsymbol{Q} \in \mathbb{R}^{n_{q} \times d_{k}}$，键 $\boldsymbol{K} \in \mathbb{R}^{n \times d_{k}}$ 和值 $V \in \mathbb{R}^{n \times d_{v}}$，其中 $n_{q}$ 是查询向量的数量，$n$ 是输入节点的数量，$d_{k}$ 是键向量的维度，和 $d_{v}$ 是值向量的维度。然后计算所有键、查询的点积，对相关值，即节点施加更多的权重，如下：$\operatorname{Att}(\boldsymbol{Q}, \boldsymbol{K}, \boldsymbol{V})=w\left(\boldsymbol{Q} \boldsymbol{K}^{T}\right) \boldsymbol{V}$，其中 $w$ 是一个激活函数。我们可以进一步使用多头注意力，而不是计算单一注意力，分别通过线性投影查询 $Q$、键 $K$ 和值$V$ $h$次，产生 $h$ 个不同的表示子空间。则多头注意函数(MH)的输出可表示如下：

　　　　$\begin{array}{left}\operatorname{MH}(\boldsymbol{Q}, \boldsymbol{K}, \boldsymbol{V})=\left[O_{1}, \ldots, O_{h}\right] \boldsymbol{W}^{O} ; \\O_{i}=\operatorname{Att}\left(\boldsymbol{Q} \boldsymbol{W}_{i}^{Q}, \boldsymbol{K} \boldsymbol{W}_{i}^{K}, \boldsymbol{V} \boldsymbol{W}_{i}^{V}\right)\end{array}$

　　其中：

• • $h$ 可以通过并行运算　　
  • 查询 $\boldsymbol{Q} \in \mathbb{R}^{n_{q} \times d_{k}}$，及 $\boldsymbol{W}_{i}^{Q} \in \mathbb{R}^{d_{k} \times d_{k}}$
  • 键 $\boldsymbol{K} \in \mathbb{R}^{n \times d_{k}}$ ，及 $\boldsymbol{W}_{i}^{K} \in \mathbb{R}^{d_{k} \times d_{k}}$
  • 值 $V \in \mathbb{R}^{n \times d_{v}}$，及 $\boldsymbol{W}_{i}^{V} \in \mathbb{R}^{d_{v} \times d_{v}}$
  • 输出投影矩阵：$\boldsymbol{W}^{O} \in \mathbb{R}^{h d_{v} \times d_{\text {model }}}$，$d_{\text {model }}$ 代表着多头注意力（MH）输出维度

　　多头注意力虽然考虑了节点之间的重要性，但是次优的生成了 键（key）和值（value），因为它从 $\text{Eq.1}$ 得到的节点嵌入 $H$ 线性投影得到键（key）和值（value）。

　　　　$\boldsymbol{H}_{u}^{(l+1)}=\operatorname{UPDATE}^{(l)}\left(\boldsymbol{H}_{u}^{(l)}, \operatorname{AGGREGATE}^{(l)}\left(\left\{\boldsymbol{H}_{v}^{(l)}, \forall v \in \mathcal{N}(u)\right\}\right)\right) \quad\quad\quad(1)$

　　为了解决这一限制，本文新定义了一种新的图多头注意块(GMH)。形式上，给定节点特征 $\boldsymbol{H} \in \mathbb{R}^{n \times d}$ 及其邻接信息 $A$，我们使用 GNNs 构造键和值，以显式地利用图结构如下：

　　　　$ \begin{array}{left}\operatorname{GMH}(\boldsymbol{Q}, \boldsymbol{H}, \boldsymbol{A})=\left[O_{1}, \ldots, O_{h}\right] \boldsymbol{W}^{O} ; \\O_{i}=\operatorname{Att}\left(\boldsymbol{Q} \boldsymbol{W}_{i}^{Q}, \operatorname{GNN}_{i}^{K}(\boldsymbol{H}, \boldsymbol{A}), \operatorname{GNN}_{i}^{V}(\boldsymbol{H}, \boldsymbol{A})\right)\end{array} \quad\quad\quad(6)$ 

　　其中，对于 Att 中的键、值矩阵，与 $\text{Eq.5}$ 中的线性投影节点嵌入 $\boldsymbol{K} \boldsymbol{W}_{i}^{K}$ 和 $\boldsymbol{V} \boldsymbol{W}_{i}^{V}$ 相比，$\mathrm{GNN}_{i}$ 的输出包含图的邻近信息。

Graph Multiset Pooling with Graph Multi-head Attention

 　　给定从GNN 获得的节点特征矩阵 $\boldsymbol{H} \in \mathbb{R}^{n \times d}$ ，定义一个 Graph Multiset Pooling （GMPool ），将 $n$ 个节点压缩为 $k$ 个典型节点，使用参数化的种子矩阵 $\boldsymbol{S} \in \mathbb{R}^{k \times d}$，用于直接以端到端方式进行优化的池化操作，如 Figure 2-GMPool ：

　　　　$\begin{array}{left}\boldsymbol{Z}=\mathrm{LN}(\boldsymbol{S}+\operatorname{GMH}(\boldsymbol{S}, \boldsymbol{H}, \boldsymbol{A}))\\\operatorname{GMPool}_{k}(\boldsymbol{H}, \boldsymbol{A})=\mathrm{LN}(\boldsymbol{Z}+\mathrm{rFF}(\boldsymbol{Z})) ; \end{array}  \quad\quad\quad(7)$ 

　　其中：rFF 是独立处理每个单独行的任何行前馈层，LN 是一个层的标准化。

　　注意，$\text{Eq.7}$ 中的 GMH 函数考虑了 $S$ 中的 $k$ 个种子向量（查询）和 $H$中的 $n$ 个节点（键）之间的相互作用，将 $n$ 个节点压缩为 $k$ 个簇，以及查询和键之间的注意力相似性。此外，为了将池化方案从集合扩展到多集，我们只需考虑冗余节点表示。

　　

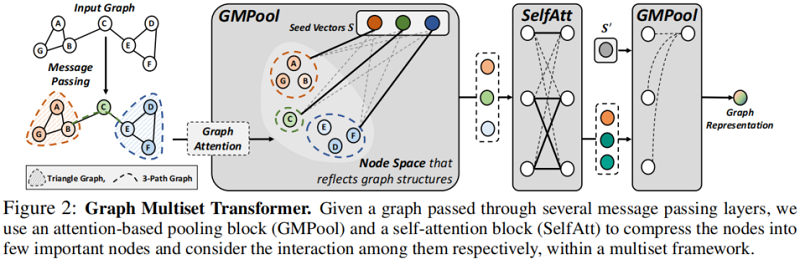
Self-Attention for Inter-node Relationship

　　虽然前面描述的 GMPool 将整个节点压缩为 $k$ 个具有代表性的节点，但该方案的一个主要缺点是它没有考虑节点之间的关系。为了解决这一限制，我们应该进一步考虑 $n$ 个或压缩的 $k$ 个不同节点之间的相互作用。

　　为此，提出了自注意力函数（SelfAtt），如 Figure 2-SelfAtt 所示：

　　　　$\begin{array}{left}\boldsymbol{Z}=\mathrm{LN}(\boldsymbol{H}+\operatorname{MH}(\boldsymbol{H}, \boldsymbol{H}, \boldsymbol{H}))\\\operatorname{SelfAtt}(\boldsymbol{H})=\operatorname{LN}(\boldsymbol{Z}+\operatorname{rFF}(\boldsymbol{Z})) ; \end{array} \quad\quad\quad(8)$ 

　　其中，与 $\text{Eq.7}$ 中考虑 $k$ 个向量和 $n$ 个节点之间相互作用的 GMH 相比，SelfAtt 通过将节点嵌入 $H$ 放在 $\text{Eq.8}$ 的MH中的查询和关键位置来捕获 $n$ 个节点之间的相互关系。为了满足 SelfAtt 的单射特性，它可能不考虑 $n$ 个节点之间的相互作用。

Overall Architecture

　　对于具有节点特征 $X$ 和邻接矩阵 $A$ 的图 $G$，编码器：$G \mapsto \boldsymbol{H} \in \mathbb{R}^{n \times d}$ 表示如下：

　　　　$\operatorname{Encoder}(\boldsymbol{X}, \boldsymbol{A})=\mathrm{GNN}_{2}\left(\mathrm{GNN}_{1}(\boldsymbol{X}, \boldsymbol{A}), \boldsymbol{A}\right) \quad\quad\quad(9)$ 

　　从编码器获得一组节点特征 $\boldsymbol{H} $ 后，池化层将这些特征聚合成单一的向量形式。池化：$\boldsymbol{H}, \boldsymbol{A} \mapsto \boldsymbol{h}_{G} \in \mathbb{R}^{d}$。为了处理大量的节点，我们首先用图多集池(GMPool)将整个图压缩为 $k$ 个具有代表性的节点，这也能适应不同大小的节点，然后利用它们之间的节点与自注意块(SelfAtt)的交互作用。最后，我们使用 $k=1$ 的 GMPool 得到整个图表示如下：

　　　　$\left.\operatorname{Pooling}(\boldsymbol{H}, \boldsymbol{A}\right)=\mathrm{GMPool}_{1}\left(\operatorname{SelfAtt}\left(\operatorname{GMPool}_{k}(\boldsymbol{H}, \boldsymbol{A})\right), \boldsymbol{A}^{\prime}\right) \quad\quad\quad(10)$ 

　　其中，$\boldsymbol{A}^{\prime} \in \mathbb{R}^{k \times k}$ 是粗化的邻接矩阵，因为邻接信息应该在用 $GMPool_k$ 将节点从 $n$ 压缩到 $ k$ 后进行调整。

2.3 Connection With Weisfeiler-lehman Graph Isomorphism Test

　　Weisfeiler-Lehman (WL) test 以其能够有效地区分两种不同的图而闻名，通过在多集上使用单射函数将两个不同的图映射到不同的空间。

　　Theorem 1 (Non-isomorphic Graphs to Different Embeddings). Let $\mathcal{A}: \mathcal{G} \rightarrow \mathbb{R}^{d}$ be a G N N , and Weisfeiler-Lehman test decides two graphs $G_{1} \in \mathcal{G}$ and $G_{2} \in \mathcal{G}$ as non-isomorphic. Then, $\mathcal{A}$ maps two different graphs $G_{1}$ and $G_{2}$ to distinct vectors if node aggregation and update functions are injective, and graph-level readout, which operates on a multiset of node features $\left\{\boldsymbol{H}_{i}\right\}$, is injective.
　　Lemma 2 (Injectiveness on Graph Multiset Pooling). Assume the input feature space $\mathcal{H}$ is a countable set. Then the output of $\operatorname{GMPool}_{k}^{i}(\boldsymbol{H}, \boldsymbol{A})$ with $G M H\left(\boldsymbol{S}_{i}, \boldsymbol{H}, \boldsymbol{A}\right)$ for a seed vector $\boldsymbol{S}_{i}$ can be unique for each multiset $\boldsymbol{H} \subset \mathcal{H}$ of bounded size. Further, the output of full GMPool $(\boldsymbol{H}, \boldsymbol{A})$ constructs a multiset with $k$ elements, which are also unique on the input multiset $\boldsymbol{H}$ .

2.4 Connection with node clustering approaches

　　节点聚类被广泛用于分层地粗化图，如 $\text{Eq.4}$ 所述。然而，由于它们需要存储甚至将邻接矩阵 $A$ 与软赋值矩阵 $\boldsymbol{C}: \boldsymbol{A}^{(l+1)}=\boldsymbol{C}^{(l)^{T}} \boldsymbol{A}^{(l)} \boldsymbol{C}^{(l)}$ 相乘，它们需要 $n$ 个节点的一个二次空间 $\mathcal{O}\left(n^{2}\right)$，这对于大图来说是有问题的。同时，我们的 GMPool 不计算一个粗化的邻接矩阵 $A^{(l+1)}$，这样图池只有在稀疏实现时才可能实现，如 Theorem 4 中形式化的那样。

　　Theorem 4 (Space Complexity of Graph Multiset Pooling). Graph Multiset Pooling condsense a graph with  n  nodes to  $k$  nodes in  $\mathcal{O}(n k)$  space complexity, which can be further optimized to  $\mathcal{O}(n) $.

　　Proposition 5 (Approximation to Node Clustering). Graph Multiset Pooling $GMPool_k$ can perform hierarchical node clustering with learnable k cluster centroids by Seed Vector  S  in $\text{Eq.7}$.

3 Experiment

　　

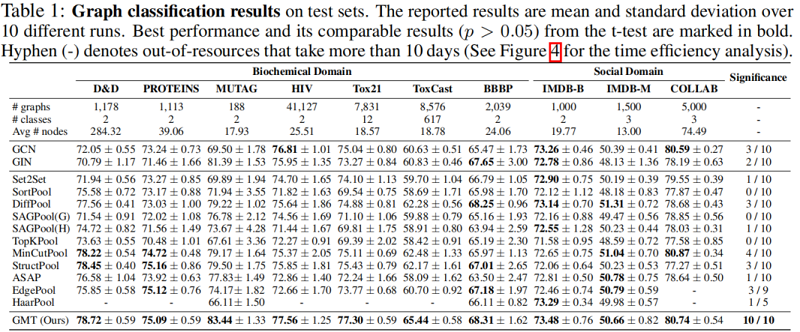
4 Conclusion

　　在这项工作中，我们指出，现有的图池方法要么不考虑每个节点的任务相关性（和或平均值），要么可能不满足注入性（节点下降和聚类方法）。克服这些限制，我们提出了一种新颖的图池方法，图多集变压器(GMT)，不仅编码给定的节点嵌入作为多集唯一地嵌入两个不同的图嵌入两个不同的嵌入，但还考虑图的全局结构和他们的任务相关性在压缩节点特性。我们从理论上证明了所提出的池化函数与WL测试一样强大，并且可以扩展到节点聚类方案中。我们在10个图分类数据集上验证了所提出的GMT，我们的方法在大多数数据集上优于最先进的图池模型。我们进一步表明，我们的方法在图重建和生成任务上优于现有的图池方法，后者需要比分类任务更准确的图表示。我们坚信，所提出的池化方法将带来实质性的实际影响，因为它通常适用于许多正在变得越来越重要的图形学习任务。