论文解读（DGB）《Self-supervised Graph Representation Learning via Bootstrapping》

论文信息

论文标题：Self-supervised Graph Representation Learning via Bootstrapping
论文作者：Feihu Che, Guohua Yang, Dawei Zhang, Jianhua Tao, Pengpeng Shao, Tong Liu
论文来源：2020, Neurocomputing
论文地址：download 
论文代码：download

1 介绍

 　　不使用负样本的对比学习。

2 方法

　　Deep Graph Bootstrapping(DGB) 的框架如下：

　　

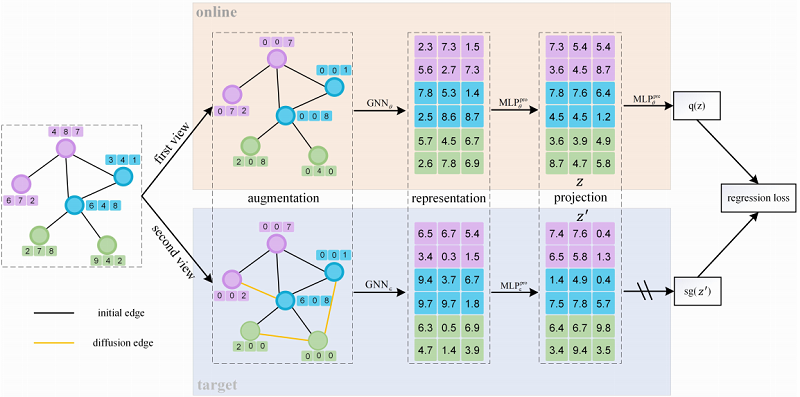
2.1 Encoder

　　$H^{(l+1)}=\sigma\left(\tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}} H^{(l)} W^{(l)}\right)$

2.2 数据增强

　　节点数据增强：

　　node dropout (ND)　　　　　　　　$\widetilde{\mathrm{X}}_{i}=\frac{\tilde{\epsilon}_{i}}{1-\delta_{n d}} \mathrm{X}_{i}$

　　node feature dropout (NFD)　　　　$\tilde{\mathrm{X}}_{i j}=\frac{\tilde{\epsilon}_{i j}}{1-\delta_{n f d}} \mathrm{X}_{i j}$

　　其中：$\delta_{n d}$ 和 $\delta_{n f d}$ 是 ND 和 NFD 各自的丢弃概率，$\tilde{\epsilon}_{i}$ 和 $\tilde{\epsilon}_{i j}$ 分别从伯努利分布 $\left(1-\delta_{n d}\right)$、$\left(1-\delta_{n f d}\right) $ 中提取。

　　邻接矩阵增强：

　　　　$S=\sum\limits _{k=0}^{\infty} \theta_{k} \mathbf{T}^{k}\quad\quad\quad(4)$

　　　　$\mathbf{S}^{\text {heat }}=\exp \left(t \mathbf{A} \mathbf{D}^{-1}-t\right)\quad\quad\quad(5)$

　　　　$\mathbf{S}^{\mathrm{ppr}}=\alpha\left(\mathbf{I}_{n}-(1-\alpha) \mathbf{D}^{-1 / 2} \mathbf{A} \mathbf{D}^{-1 / 2}\right)^{-1}\quad\quad\quad(6)$

2.3 训练方式

　　指数移动平均

 　　　　$\xi \leftarrow p \xi+(1-p) \theta\quad\quad\quad(7)$

2.4 损失函数

　　$\bar{q}(z) \triangleq q(z) /\|q(z)\|_{2}\theta\quad\quad\quad(8)$

　　$\bar{z}^{\prime} \triangleq z^{\prime} /\left\|z^{\prime}\right\|_{2}\theta\quad\quad\quad(9)$

　　$\mathcal{L}_{\theta}^{\text {DGB }} \triangleq\left\|\bar{q}(z)-\bar{z}^{\prime}\right\|_{2}^{2}\theta\quad\quad\quad(10)$

3 实验

数据集

　　

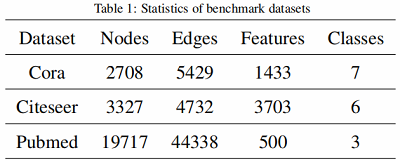
实验结果

　　

　　

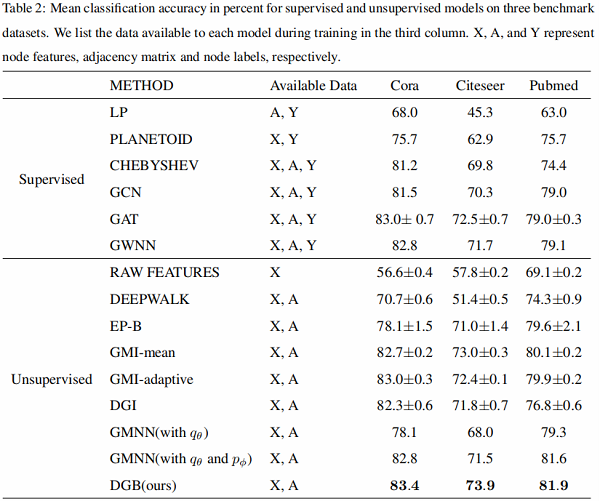
 　　更多细节，请参考论文解读（SelfGNN）《Self-supervised Graph Neural Networks without explicit negative sampling》