图神经网络的攻击防御
一、图神经网络的鲁棒性简介
图神经网络的鲁棒性研究基本上是跟随了卷积神经网络里的鲁棒性研究。给定一张图片,如下所示,可以将其放入CNN模型里,训练好的CNN模型可以给我们不错的效果。但是如果我们给图片加入微小的扰动 $\varepsilon$ (肉眼可能无法识别的扰动),CNN模型可能就会受到欺骗,给出错误的结果。一般来说,这种微小的扰动 $\varepsilon$ 并不是随机生成的(随机生成的如高斯分布生成的误差 $\varepsilon$ ,模型的识别能力不会受很大影响),而是根据算法特意的去生成的,这种特意生成的过程称为对抗攻击。
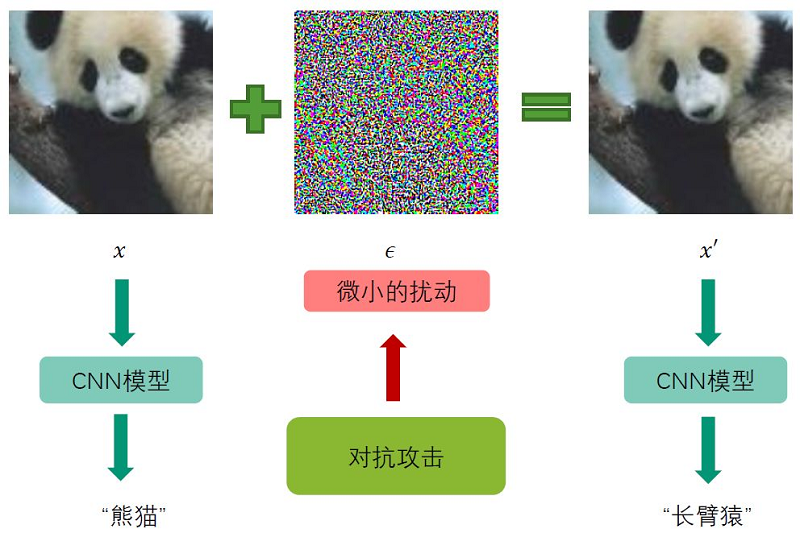
研究表明,图神经网络沿袭了卷积神经网络不鲁棒的特征。假设一个节点分类任务,在未受到扰动的GNN中,模型给定一个预测的结果,给定扰动之后(这个扰动可以是增加一条不存在的边,减少一条存在的边,增加一个不存在的节点,减少一个存在的节点等),模型给出的结果可能发生变化。通过一点扰动就可以改边模型的结果,这样的风险在生物医学、金融等安全领域造成的后果是非常严重的。因此在欺诈检测、金融违约预测等方面对GNN鲁棒性的研究是较多的。

通过前面的叙述可以得知,图对抗攻击通过生成“不容易”察觉的微小扰动来降低GNN的效果,了解图对抗攻击可以帮助我们明白降低GNN效果的原因,对GNN的稳定性和鲁棒性的理解更加深入。图对抗防御则是用来减少扰动带来的影响。
二、图对抗攻击
图对抗攻击通过生成“不容易”察觉的微小扰动来降低GNN的效果。这里的微小的扰动可以分为图结构的扰动和节点特征的扰动。
图结构的扰动和节点特征的扰动。GNN的输入一般就是邻接矩阵 $A$ 和节点的特征矩阵 $X$ 。对 图结构的扰动对应的就是对邻接矩阵进行扰动 $\Delta A$ ,扰动后 $A^{\prime}$ 。对节点特征的扰动对应的就 是对特征矩阵进行扰动 $\Delta X$ ,扰动后 $X^{\prime}$ 。一般而言,扰动是微小的,所以就需要限制扰动的 程度,对应有不同的方法来生成扰动。通常进行扰动的一种标注就是满足如下的公式:
$\left\|A^{\prime}-A\right\|_{0}+\left\|F^{\prime}-F\right\|_{0} \leq \Delta$
更具体一点,扰动的类型在图的结构上,体现为加边、减边、加节点,在特征上,可以更改特征的数值。
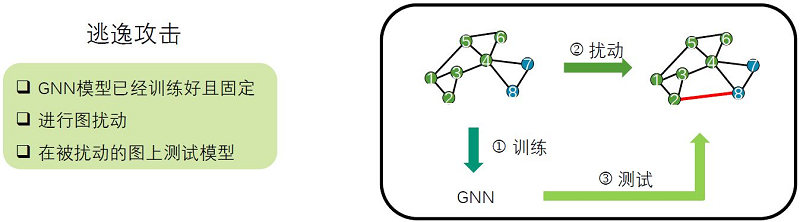
攻击的类型根据扰动在训练的前后分为逃逸攻击(evasion attack)和投毒攻击(poisoning attack)。逃逸攻击(evasion attack)是指对训练好的模型进行攻击,此时攻击者不能修改模型的参数或是结构。如下图所示,第一步,模型首先在一张干净的没有被攻击过的图上进行训练,已经训练好且固定了。第二步,对图进行扰动,比如加边减边等,第三步,在扰动后的图上进行测试。逃逸攻击不会干扰到训练的数据,只是在测试阶段产生影响。在图片领域中,自动驾驶汽车、物联网设备、语音识别系统等都可以应用逃逸攻击。人脸识别中,原始图中没有眼镜的人,带了眼镜之后,模型可能识别效果就会出错。GNN中也同样如此。
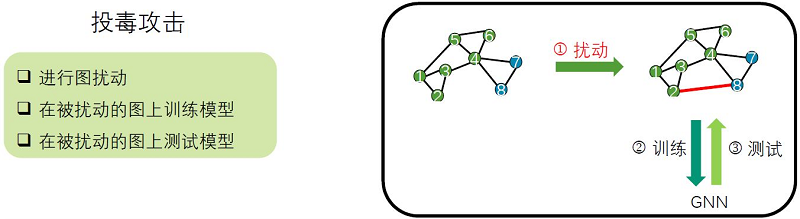
另一种攻击的类型为投毒攻击(poisoning attack)是指在模型训练前进行攻击,此时攻击者可以在训练数据中插入”毒药”从而干扰模型的训练过程。如下图所示,它会对训练数据进行干扰。第一步,就对训练数据进行扰动,比如加边减边等,第二步,GNN模型在被扰动的图上做训练,第三步,在被扰动的图上测试模型。在推荐系统中很容易受到投毒攻击,向推荐系统注入虚假数据,从而使推荐系统按照攻击者的意愿做推荐。
了解了攻击类型或者攻击场景,可以根据攻击者对GNN模型的了解,将模型分为白盒攻击(white-box attack)、灰盒攻击(grey-box attack)和黑盒攻击(black-box attack)。GNN的模型有训练数据、模型结构和模型参数等知识,白盒攻击表示攻击者可以获得被攻击模型的完整信息,所有的信息都是已知的。一般来说,这种情况是不现实的,攻击者没有知道全部信息的能力,但是白盒攻击对图神经网络稳定性的研究还是有意义的。灰盒攻击表示攻击者可以获得被攻击的模型的训练数据,其他的如模型的结构和参数等是不知道的。黑盒攻击则是攻击者不能知道被攻击模型的任何信息,只允许从目标模型中进行查询来获得结果。下面将列举三种类型攻击的常见方法:
1.白盒攻击
(1)PGD拓扑攻击:PGD拓扑攻击是通过扰动图的结构来进行攻击的方式。通过对图结构的改变,使得最终预测的结果发生改变,节点 $v_{i}$ 的类别 $y_{i}$ 改变。
用符号表示如何扰动图的结构。 $A$ 表示图的邻接矩阵, $\bar{A}$ 表示 $A$ 的补,当 $A_{i j}=1$ 时, $\overline{A_{i j}}=0$ ,当 $A_{i j}=0$ 时, $ \overline{A_{i j}}=1$ 。扰动可以公式表示:
$\Delta A=(\bar{A}-A) \odot S $
这里的 $(\bar{A}-A)$ 元素为 $1$ 或 $-1$ , $1$ 表示可以增加的边, $-1$ 表示可以减去的边。 $S \in\{0,1\}^{N \times N}$ 为对称布尔矩阵,表示需要改动哪些边,这个矩阵是攻击者需要学习的, $\odot$ 为矩阵的 Hadamand乘积。扰动过后的结果 $A^{\prime}=A+\Delta A $。
PGD 拓扑攻击的基本思想就是通过学习对 $S$ 来实现修改节点 $v_{i}$ 的类别。对于给定的 $S$ 矩阵和 参数固定的GNN我们可以正向计算节点 $v_{i}$ 的分类概率 $z_{i}$ 。记 $v_{i}$ 真实的标签为 $y_{i}$ ,我们希 望扰动后的类别 $y_{i}$ 的概率不再是最大值,因此可以构造损失函数:
$l\left(v_{i}\right)=z\left[y_{i}\right]-\max _{c \neq y_{i}} z[c]$
最小化每一个节点的标签与标签之外的另一个类别的概率之差, $\max _{c \neq y_{i}} z[c]$ 表示标签类别 $y_{i}$ 之外的类别的概率最大值,使得扰动之后的节点更容易分错类别。有时候,损失到一定的程度 就可以,也就是说两者之间的概率差达到一定的阈值就可以实现攻击的意图。因此,可以对损失函 数进行一个改进:
$l\left(v_{i}\right)=\max \left\{z\left[y_{i}\right]-\max _{c \neq y_{i}} z[c],-\kappa\right\}$
参数 $\kappa>0$ ,这里的限制与知识图谱表征 Trans 系列模型的限制是相似的。有了损失函数之 后,利用反向传播和梯度下降(Projected Gradient Descent)来更新矩阵 $S$ ,首先对损失函数 进行梯度下降,得到的结果是取值任意的实数 $S^{\prime} \in R^{N \times N}$ ,并非是 $[0,1]^{N \times N}$ ,通过一步投 影的步骤Projected,将结果转换为 0 到 1 之间,从而得到取值介于 $[0,1]$ 之间的矩阵 $S^{\prime} \in[0,1]^{N \times N}$ ,其中的元素可以当作采样概率,通过采样获取实际的扰动矩阵,整个模型的 流程如下:

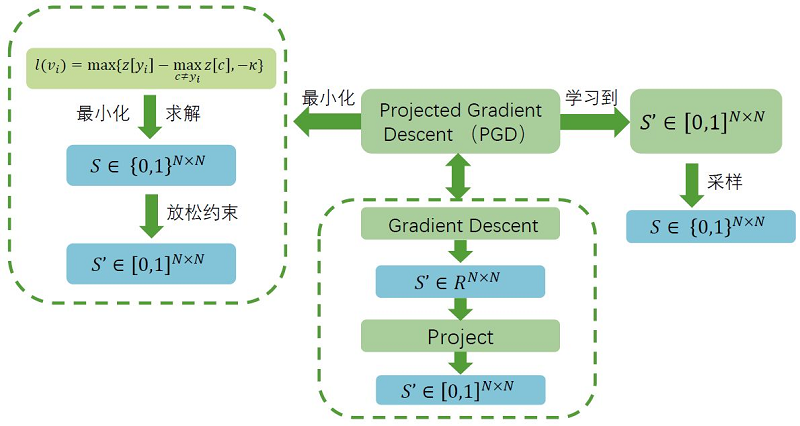
(2) 基于积分梯度的攻击
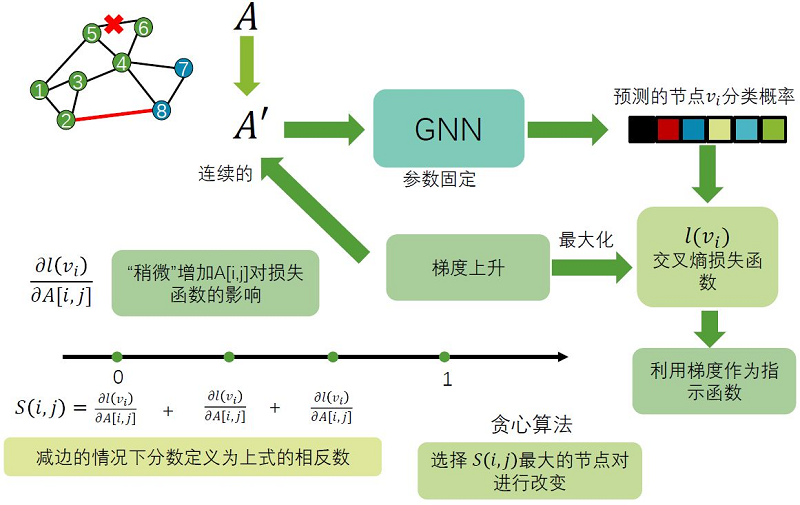
这种方法既可以对图结果进行攻击,也可以对特征进行攻击。当然,这里的特征有限制,设定其都 是二值的特征,对特征进行 $0$ 与 $1$ 互换的扰动。假设我们跟PGD拓扑攻击一样的设定,对节点 邻接矩阵 $A$ 进行扰动,我们希望攻击节点分类任务,对于某个标签为 $y_{i}$ 的节点,攻击者想让 GNN把它分类为其他标签,从而损失函数将交叉熵最大化。因此利用梯度上升最大化节点 $v_{i}$ 的 交叉熵来降低模型性能。但邻接矩阵是离散的,无法直接使用基于梯度的方法,从而可以推广到 $[0,1]$ 区间。
$S_{i j}=\frac{\partial l(v)}{\partial A_{i j}}$ 表示对邻接矩阵某个元素扰动之后的损失函数的变化情况。将偏导数在 [0,1] 区 间上不同位置的取值相加(类似于积分,离散的相加)作为指示函数,这样的 $S_{i j}$ 可以作为一种得 分,衡量对损失函数增大的帮助。对于加边的情况,用以上的算法计算,减边的情况,取相反数可 以得到相同的效果。以上定义好了,使用贪心算法,遍历任意节点的扰动,选择 $S_{i j}$ 最大的情况 得到结果。整个模型的流程如下:
2 灰盒攻击
灰盒攻击,攻击者不能得到被攻击模型的结构和参数,只能得到训练的数据。灰盒攻击通常不是直接攻击给定的模型,而是首先利用训练数据训练一个代理模型,然后攻击这个代理模型。
(1) Nettack
它的攻击是生成针对节点分类任务的对抗图,对于攻击目标 $v_{i}$ 以及它的类别 $y_{i}$ ,Nettack试图 修改图的邻接矩阵和节点特征使得GNN将 $v_{i}$ 分类为其它的标签,同时修改后对邻接矩阵以及节点 特征的扰动要尽可能小:
$\left\|A^{\prime}-A\right\|_{0}+\left\|F^{\prime}-F\right\|_{0} \leq \Delta$
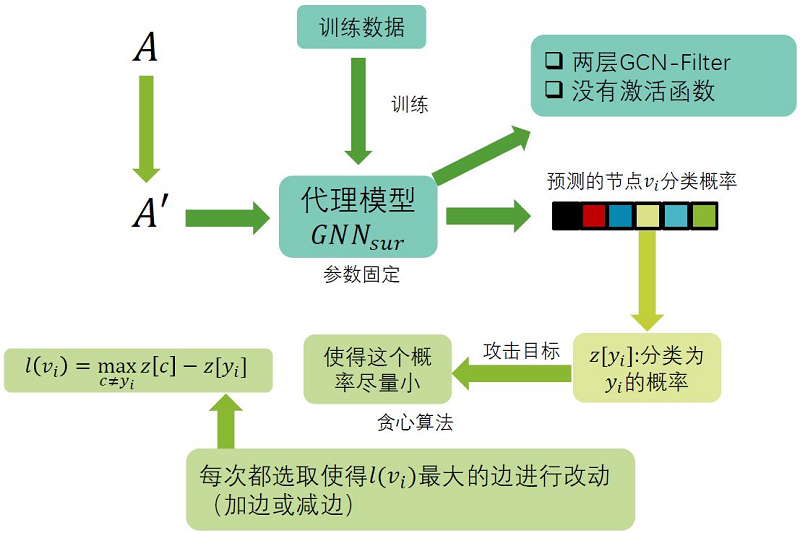
除此之外,Nettack还要求新图的度的分布以及特征共现与原图要尽可能接近。Nettack首先对训练数据训练一个参数固定代理模型 $G N N_{s u r}$ ,它是没有激活函数的两层 GCN-Filter,可以认为是简化版的GCN模型。有了模型与数据,Nettack攻击代理模型,使得原本的分类概率尽可能的
$l\left(v_{i}\right)=\max _{c \neq y_{i}} z[c]-z\left[y_{i}\right]$
这里最大化目标函数,Nettack会选择使 $l\left(v_{i}\right)$ 变化最大的一条边进行增加或删除的改动,特征的改动也是类似。整个算法的框架如下:
(2) Meta Attack
Meta Attack同样是一种针对节点分类任务的灰盒攻击攻击方法。与 Nettack 不同的是,在Meta Attack中,攻击者希望降低GNN在测试集上的整体分类性能。攻击限制与Nettack相同, $\left\|A^{\prime}-A\right\|_{0}+\left\|F^{\prime}-F\right\|_{0} \leq \Delta$ ,度的分布与特征共现。这两篇文章都是出自同一作者。 Meta Attack是一种投毒攻击,在被扰动的图上训练和测试模型。
Meta Attack首先需要训练代理模型 $G N N_{s u r}$ ,但与Nettack不同的地方在于代理模型需要分 别在原始数据以及投毒后的数据上进行训练。在原始数据上的训练结果相当于给定了结果标准,代 理模型中的结果是被投毒后的预测结果。Meta Attack的攻击目标是使同样结构的模型在扰动前后 的数据上有较大的差异,即最大化节点类别的交叉熵:
$L_{s e l f}=L\left(f_{G N N}\left(A^{\prime} ; \Theta^{*}\right), C_{u}^{\prime}\right)$
其中 $C_{u}^{\prime}$ 是代理模型在原始数据上对节点的预测标签。在原始论文中还添加了代理模型在被投毒 数据集上的交叉熵,从而得到最终的损失函数:
$L_{a t k}=-L_{s e l f}-L_{t r}\left(A^{\prime}\right)$
Meta Attack的本质是求解如下定义的双层优化问题:
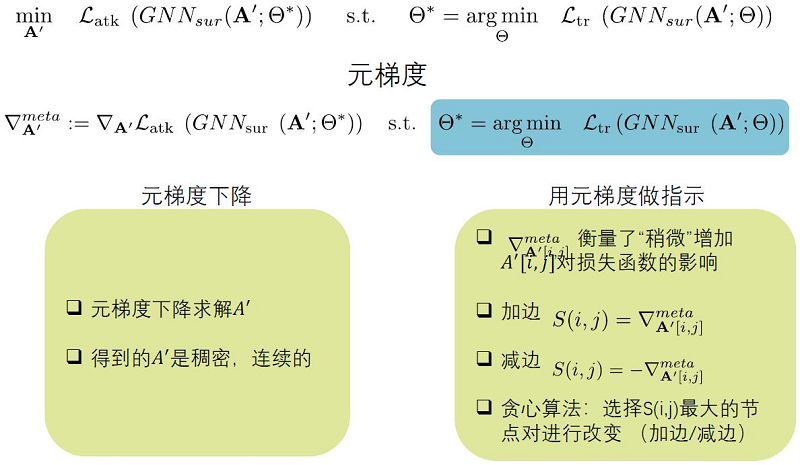
$\begin{array}{l}\min _{A^{\prime}} \mathscr{L}_{a t k}\left(G N N_{s u r}\left(A^{\prime} ; \Theta^{*}\right)\right) \\\text { s.t. } \Theta^{*}=\operatorname{argmin}_{\Theta} \mathscr{L}_{t r}\left(G N N_{s u r}\left(A^{\prime} ; \Theta\right)\right)\end{array}$
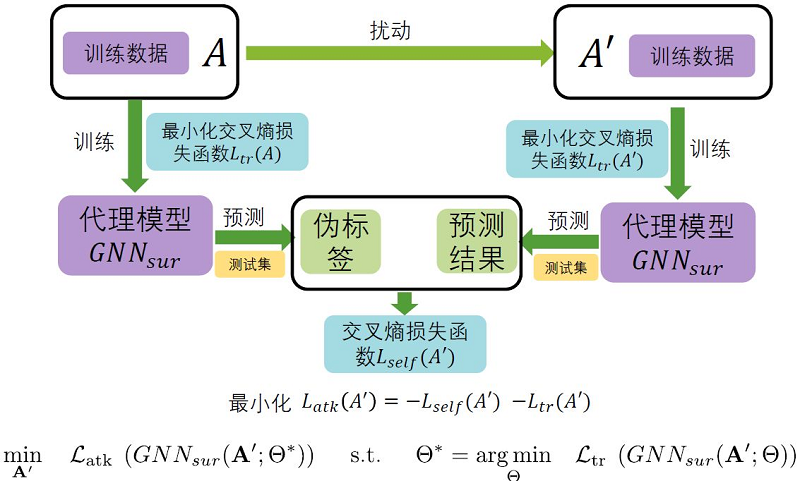
下面看一下上式如何求解。首先是求解最优的代理模型,然后在最优的代理模型的基础上怎样使攻击的效果达到最好。具体的求解过程可以通过论文或其他资料再进行学习。
3 黑盒攻击
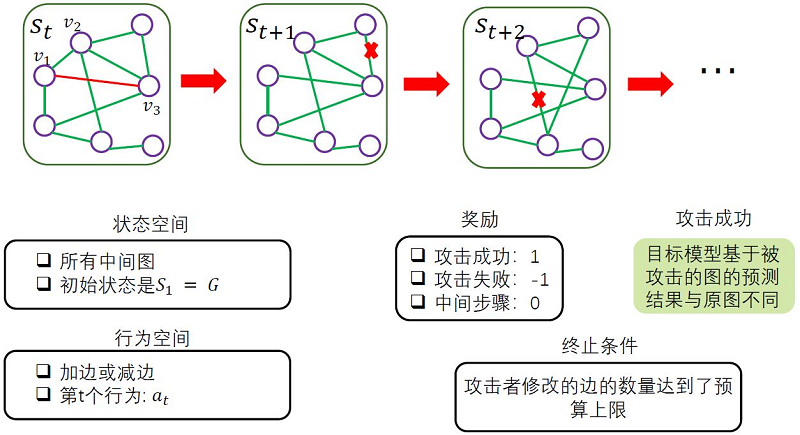
黑盒攻击,此时攻击者无法获知关于受害模型的任何信息而只能查询受害模型给出的预测结果。黑盒攻击的一种思路是把攻击建模成一个马尔科夫决策过程,当前的决策只基于当前的状态而与之前的决策无关,根据攻击后受害模型的反馈来设计奖励函数,然后通过强化学习的相关方法来求解这个问题。
三、图对抗防御
与图对抗攻击所对应的内容是图对抗防御,我们希望我们的模型能够防御针对图类型数据的对抗攻击。图对抗防御计算可以主要分为四类:图对抗训练、图净化、图注意力机制与图结构学习。
1 对抗训练
图对抗训练的基本思想是将对抗样本纳入模型的训练阶段,扩大了训练的样本,原始数据和对抗样本一同训练,从而提高模型的鲁棒性。这样的做法已经将模型不稳定的因素纳入了训练中,从而解决了这些因素。
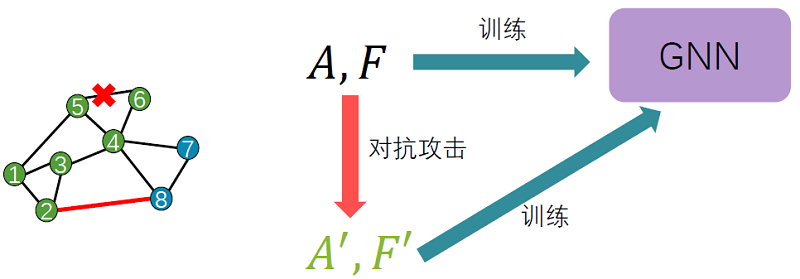
如针对图结构的对抗训练,可以将PGD拓扑攻击下的样本放入训练中。
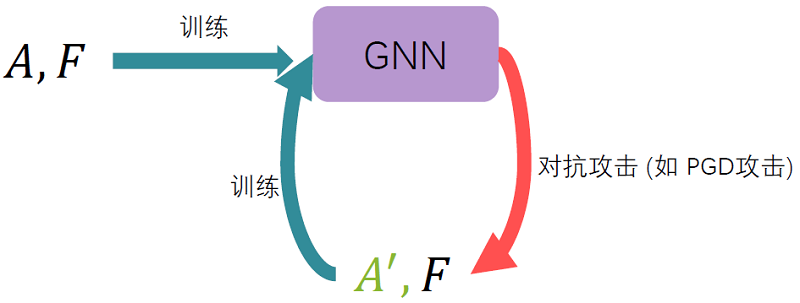
针对图结构和特征的对抗训练,将扰动加入到已经消息传递和邻域聚合之后的第一层隐藏层中,这样就达到了扰动结构和特征的效果。

2 图净化
图净化的思想是从攻击后的图数据中识别出对抗攻击的部分,并在训练模型前删除它们,从而在干净的图数据上训练模型。它代表的就是预处理的过程。
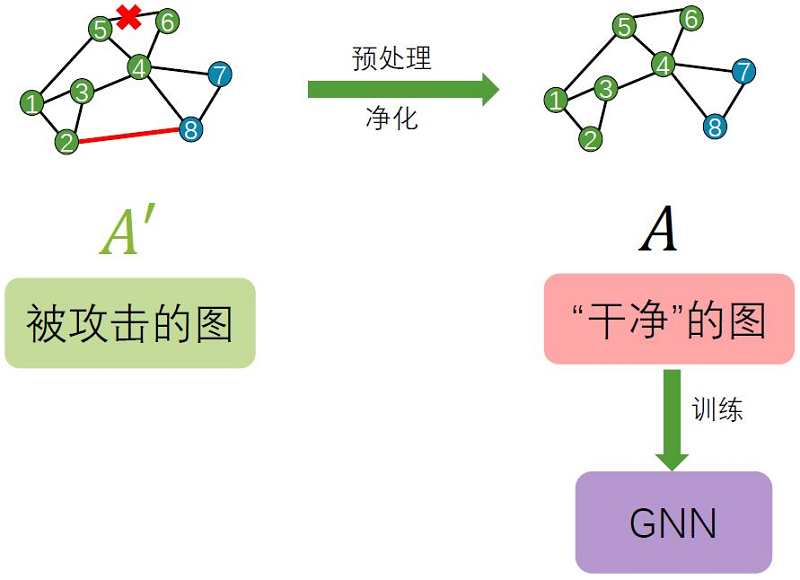
实验研究表明,很多图对抗攻击方法会倾向于添加连接特征明显不同的节点的边。因此我们可以通过阈值化的方式过滤掉特征差异很大的节点之间的边,从而完成图净化。此外一些研究还表明图对抗攻击会改变邻接矩阵的秩,因此一些研究者也提出了使用SVD来对邻接矩阵进行低秩重建来恢复攻击前的邻接矩阵。
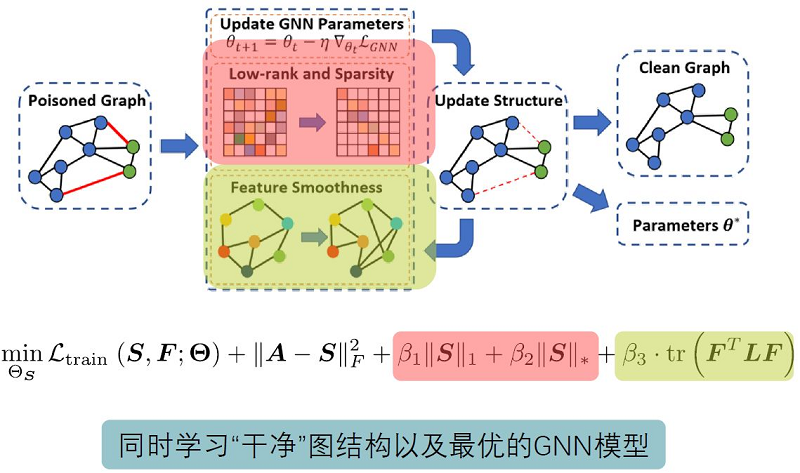
3 图结构学习
图结构学习的代表模型是Pro-GNN。图结构学习的基本思想是在训练GNN的同时更新图的结构,从而获得鲁棒的图神经网络。
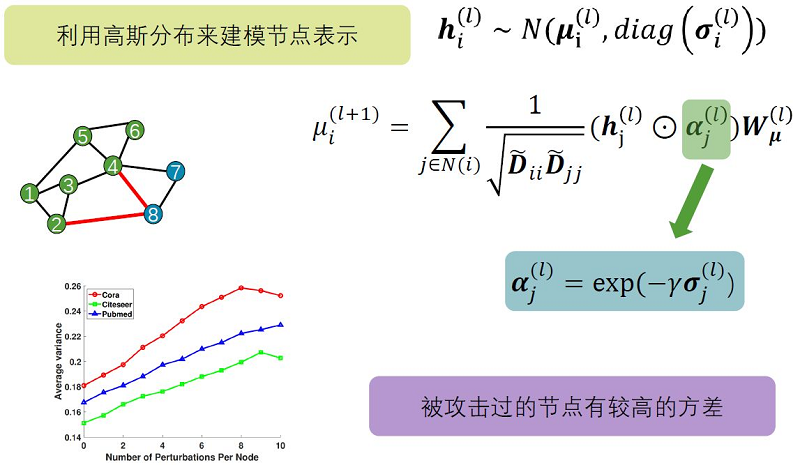
4 图注意力机制
图注意力机制的思想是使图更少地关注那些容易受到攻击的节点或边,从而减少这类节点或边的影响。在RGCN中提出了使用高斯分布来对节点表示进行建模,并通过基于方差的注意力机制来阻止对抗攻击在网络上的传播。
因上求缘,果上努力~~~~ 作者:图神经网络,转载请注明原文链接:https://www.cnblogs.com/BlairGrowing/p/16184096.html


