论文解读(SelfGNN)《Self-supervised Graph Neural Networks without explicit negative sampling》
论文信息
论文标题:Self-supervised Graph Neural Networks without explicit negative sampling
论文作者:Zekarias T. Kefato, Sarunas Girdzijauskas
论文来源:2021, WWW
论文地址:download
论文代码:download
1 Introduction
本文核心贡献:
-
- 使用孪生网络隐式实现对比学习;
- 本文提出四种特征增强方式(FA);
2 Method
2.1 Graph Data Augumentations
拓扑结构:
-
- 基于随机游走的 $\text{PageRank}$ 算法:
$\boldsymbol{H}^{P P R}=\alpha(\boldsymbol{I}-(1-\alpha) \tilde{A})^{-1} \quad\quad\quad(2)$
$\boldsymbol{H}^{H K}=\exp \left(t A D^{-1}-t\right)\quad\quad\quad(3)$
其中 $\alpha$ 是心灵传输概率 ,$t$ 是扩散时间
-
- 基于 $\text{Katz}$ 指标的算法:
$\boldsymbol{H}^{k a t z}=(I-\beta \tilde{A})^{-1} \beta \tilde{A}\quad\quad\quad(4)$
Katz-index是一对节点之间所有路径集的加权和,路径根据其长度进行惩罚。衰减系数($\beta$)决定了处罚过程。
特征增强:
-
- Split:特征 $X$ 拆分成两部分 $\boldsymbol{X}=\boldsymbol{X}[:,: F / 2]$ 和 $\boldsymbol{X}^{\prime}=\boldsymbol{X}[:, F / 2:]$ ,然后分别用于生成两个视图。
- Standardize:特征矩阵进行 z-score standardization :
${\large X^{\prime}=\left(\frac{X^{T}-\bar{x}}{s}\right)^{T}} $
其中 $\bar{x} \in \mathbb{R}^{F \times 1}$ 和 $s \in \mathbb{R}^{F \times 1}$ 是与每个特征相关联的均值向量和标准差向量。
-
- Local Degree Profile (LDP):提出了一种基于节点局部度轮廓计算出的五个统计量的节点特征构建机制 $\mathbf{X}^{\prime} \in \mathbb{R}^{N \times 5}$ ,然后使用零填充 $X^{\prime} \in \mathbb{R}^{N \times F}$ 使其维度与 $X$ 一致。
- Paste:是一种功能增强技术,它简单地结合了 $X$ 和 LDP 功能,如增强功能 $\boldsymbol{X}^{\prime} \in \mathbb{R}^{N \times(F+5)}$。在这种情况下,在原始特征矩阵 $X$ 上应用了一个零填充,例如 $X \in \mathbb{R}^{N \times(F+5)}$ 。
2.2 Framework
框架如下:
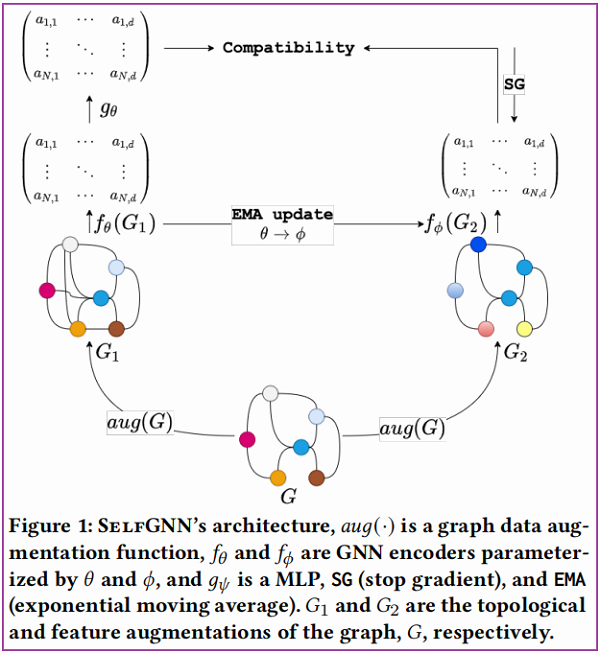
组成部分:
-
- 组件一:生成视图,$any(G)$ 是对原始图 $G$ 从拓扑或特征层面进行数据增强;
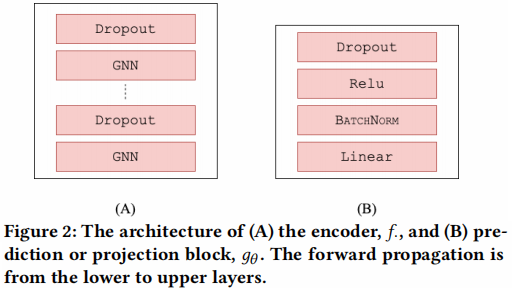
- 组件二:图自编码器 $f_{\theta}$ 和 $f_{\phi}$,一种堆叠架构,如 Figure 2 (A) 所示。概括为:$X_{1}=f_{\theta}\left(G_{1}\right)$, $X_{2}=f_{\phi}\left(G_{2}\right)$;
- 组件三:投影头,类似$g_{\theta}$的架构,如 Figure 2 (B) 所示;
须知:
只对学生网络的参数通过梯度更新(SG),学生网络使用的损失函数如下:
$\mathcal{L}_{\theta}=2-2 \cdot \frac{\left\langle g_{\theta}\left(X_{1}\right), X_{2}\right\rangle}{\left\|g_{\theta}\left(X_{1}\right)\right\|_{F} \cdot\left\|X_{2}\right\|_{F}}\quad\quad\quad(5)$
教师网络参数通过学生网络使用指数移动平均(EMA,exponential moving average)进行更新。指数移动平均如下:
$\phi \leftarrow \tau \phi+(1-\tau) \theta\quad\quad\quad(6)$
这里 $\tau$ 是衰减率。
4 Experiment
数据集:
- citation networks (Cora, Citeseer, Pubmed)
- author collaboration networks (CS, Physics)
- co-purchased products network (Photo, Computers)
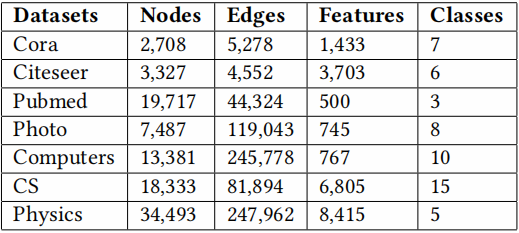
实验设置:
-
- 70/10/20–train/validation/test
- $\alpha=0.15$, $t=3$, $\beta=0.1$
- 70/10/20–train/validation/test
与原始 GNN 的比较:
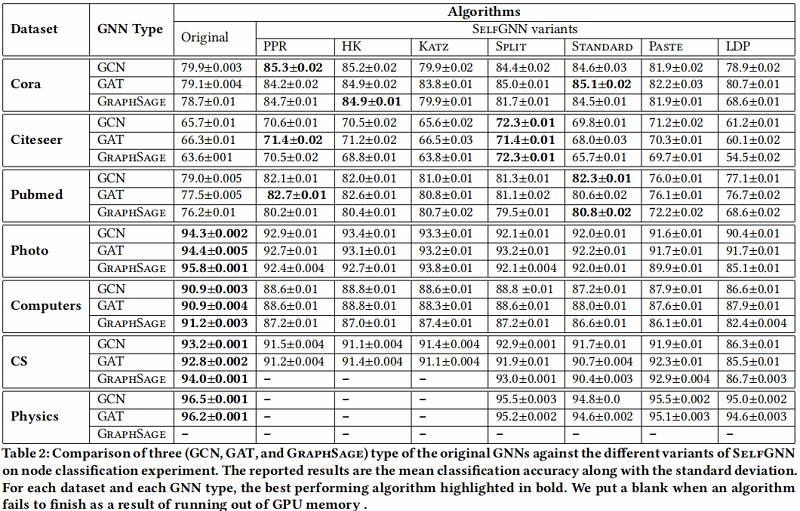
与自监督 GNN 的比较:

消融实验:
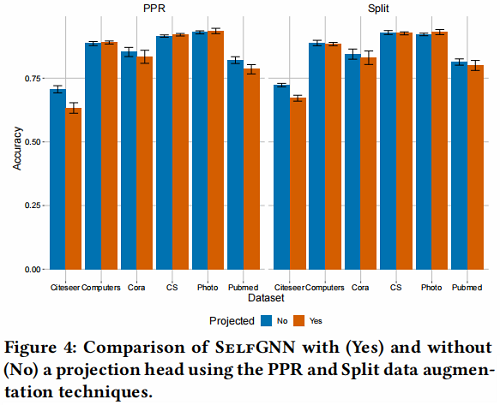
Split 策略的有效性:
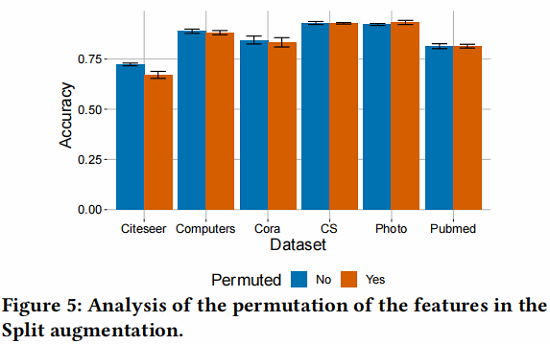
5 Conclusion
本文提出了无需负样本的对比学习框架,且提出了几种有意思的特征数据增强。
修改历史
2021-04-14 创建文章
2022-06-14 精读
因上求缘,果上努力~~~~ 作者:图神经网络,转载请注明原文链接:https://www.cnblogs.com/BlairGrowing/p/16146288.html

