论文解读（BGRL）《Large-Scale Representation Learning on Graphs via Bootstrapping》

论文信息

论文标题：Large-Scale Representation Learning on Graphs via Bootstrapping
论文作者：Shantanu Thakoor, Corentin Tallec, Mohammad Gheshlaghi Azar, Rémi Munos, Petar Veličković, Michal Valko
论文来源：2021, ICLR
论文地址：download 
论文代码：download

　　早先版本名字叫《Bootstrapped Representation Learning on Graphs》

1 Introduction

　　研究目的：对比学习中不适用负样本。

　　本文贡献：

• • 对图比学习不使用负样本

2 Method

2.1 Framework

　　 

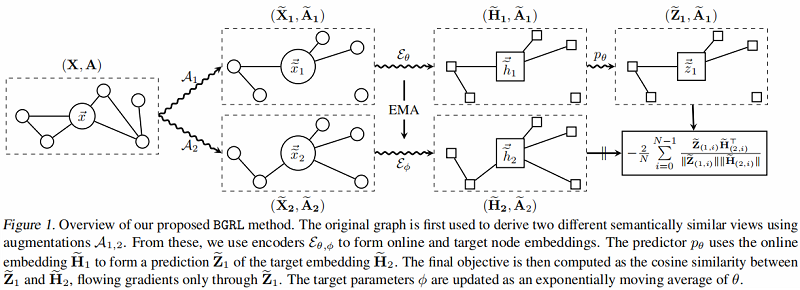
　　　　上面是 online network，下面是 target network 。

　　步骤：

• • 步骤一：分别应用随机图增强函数 $\mathcal{A}_{1}$ 和 $\mathcal{A}_{2}$，产生 $G$ 的两个视图：$\mathbf{G}_{1}=   \left(\widetilde{\mathbf{X}}_{1}, \widetilde{\mathbf{A}}_{1}\right)$ 和 $\mathbf{G}_{2}=\left(\widetilde{\mathbf{X}}_{2}, \widetilde{\mathbf{A}}_{2}\right) $；
  • 步骤二：在线编码器从其增广图中生成一个在线表示 $\widetilde{\mathbf{H}}_{1}:=\mathcal{E}_{\theta}\left(\widetilde{\mathbf{X}}_{1}, \widetilde{\mathbf{A}}_{1}\right)$；目标编码器从其增广图生成目标表示 $\widetilde{\mathbf{H}}_{2}:=\mathcal{E}_{\phi}\left(\widetilde{\mathbf{X}}_{2}, \widetilde{\mathbf{A}}_{2}\right) $；
  • 步骤三：在线表示被输入到一个预测器 $p_{\theta}$ 中，该预测器  $p_{\theta}$  输出对目标表示的预测  $\widetilde{\mathbf{Z}}_{1}:=   p_{\theta}\left(\widetilde{\mathbf{H}}_{1}, \widetilde{\mathbf{A}}_{1}\right)$，除非另有说明，预测器在节点级别工作，不考虑图信息(仅在 $\widetilde{\mathbf{H}}_{1}$ 上操作，而不是 $\widetilde{\mathbf{A}}_{1}$)。

2.2 BGRL Update Param

更新 $\theta$

　　在线参数 $\theta$，通过余弦相似度的梯度，使预测的目标表示 $\mathbf{Z}_{1}$ 更接近每个节点的真实目标表示 $\widetilde{\mathbf{H}}_{2}$。

　　　　$\ell(\theta, \phi)=-\frac{2}{N} \sum\limits _{i=0}^{N-1} {\large \frac{\widetilde{\mathbf{Z}}_{(1, i)} \widetilde{\mathbf{H}}_{(2, i)}^{\top}}{\left\|\widetilde{\mathbf{Z}}_{(1, i)}\right\|\left\|\widetilde{\mathbf{H}}_{(2, i)}\right\|}} \quad\quad\quad(1)$

　　$\theta$ 的更新公式：

　　　　$\theta \leftarrow \operatorname{optimize}\left(\theta, \eta, \partial_{\theta} \ell(\theta, \phi)\right)\quad\quad\quad(2)$

　　其中 $ \eta $ 是学习速率，最终更新仅从目标对 $\theta$ 的梯度计算，使用优化方法如 SGD 或 Adam 等方法。在实践中，

　　我们对称了训练，也通过使用第二个视图的在线表示来预测第一个视图的目标表示。

更新 $\phi$

　　目标参数 $\phi$ 被更新为在线参数 $\theta$ 的指数移动平均数，即：

　　　　$\phi \leftarrow \tau \phi+(1-\tau) \theta\quad\quad\quad(3)$

　　其中 $\tau$ 是控制 $\phi$ 与 $ \theta$ 的距离的衰减速率。

　　只有在线参数被更新用来减少这种损失，而目标参数遵循不同的目标函数。根据经验，与BYOL类似，BGRL不会崩溃为平凡解，而 $\ell(\theta, \phi)$ 也不收敛于 $0$ 。

3 Experiment

数据集

　　

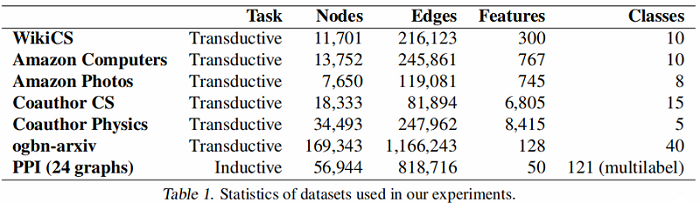
　　数据集划分：

• • WikiCS： 20 canonical train/valid/test splits
  • Amazon Computers, Amazon Photos——train/validation/test—10/10/80%
  • Coauthor CS, Coauthor Physics——train/validation/test—10/10/80%

直推式学习——基线实验

　　图编码器采用 $\text{GCN}$ Encoder 。

　　

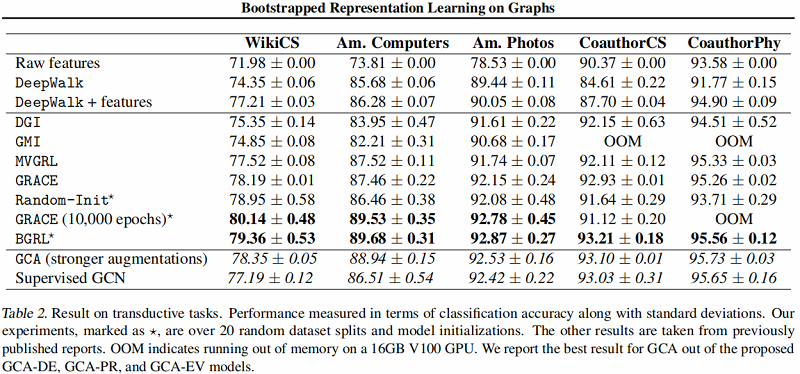
大图上的直推式学习——基线实验

　　结果：

　　

归纳式学习——基线实验

　　编码器采用 GraphSAGE-GCN （平均池化）和 GAT 。 

　　结果：

　　

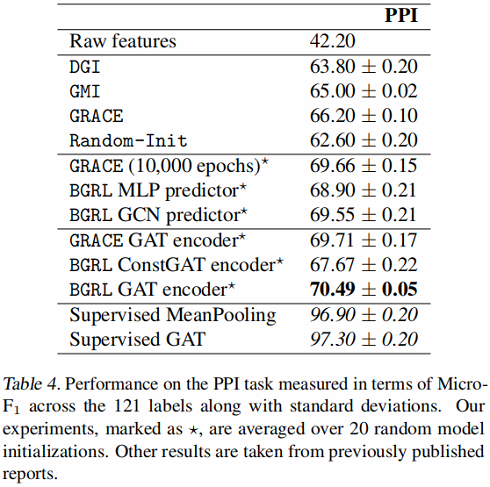
4 Conclusion

　　使用了一种简单的不需要负样本的对比学习框架。

 

修改历史

2021-04-14 创建文章
2022-06-14 精读

 

论文解读目录