论文解读（AutoSSL）《Automated Self-Supervised Learning for Graphs》

论文信息

论文标题：Automated Self-Supervised Learning for Graphs
论文作者：Wei Jin, Xiaorui Liu, Xiangyu Zhao, Yao Ma, Neil Shah, Jiliang Tang
论文来源：2022, ICLR
论文地址：download 
论文代码：download 

Abstract

　　研究现状：

• • 不同的代理任务对不同数据集的下游任务的影响不同，表明代理任务的使用对于图的自监督学习至关重要；
  • 当前工作大多基于单一的代理任务；

　　本文工作：设计多个代理任务并使用不同的权重。

1 Introduction

　　首先 Figure1 (a)(b)  给出不同的 SSL 任务在不同的数据集具有不同的下游性能的例子：

　　

　　从 Figure1 (a)(b) 这一观察结果表明，SSL任务的成功在很大程度上依赖于数据集和下游任务。用单一任务学习表征自然会导致忽略其他任务中的有用信息。

　　其次，Figure1 (c) 说明联合使用不同的SSL任务使用不同权重的的重要性。

　　那么，对于不同的SSL任务使用不同权重所要面临的问题：

• • 首先是搜索空间巨大，所以本文希望能自动学习到这些权重；　　
  • 其次，寻找最优任务权重通常需要下游性能的指导，这在无监督设置下是自然缺失的；　　

　　由于在 SSL 过程中缺乏地面真实标签，我们提出了一种伪同质性度量来评估从特定的 SSL 任务组合中训练出来的节点嵌入的质量。

　　本文贡献：

• • 为了弥合无监督表示和下游标签之间的差距，我们提出了伪同质性来衡量表示的质量。此外，在给定具有高同质性的图时，我们从理论上证明了 pseudo-homophily 最大化可以帮助最大化伪标签与下游标签之间互信息的上界。
    
  • 基于 pseudo-homophily，我们提出了两种有效搜索SSL任务的策略，一种采用 evolution algorithm，另一种通过 meta-gradient descent 进行可微搜索。Autossl能够在搜索期间调整任务的权重，如 Figure1 (d) 所示。
  • 我们通过在8个真实数据集上组合各种不同的任务来评估所提出的自动。大量的实验表明，自动可以显著改善单个任务在节点聚类和节点分类方面的性能（例如，在节点聚类方面的相对提高高达10.0%）。

2 Related work

　　以下内容不全，单纯是我存在的知识欠缺部分。

• Self-Supervised Learning in GNNs
  • 具体来说，这些SSL方法构造了一个预定义的代理任务，为未标记的节点/图分配伪标签，然后在设计的代理任务上训练模型来学习表示。以对比学习为例，基于同质性假设，相似性越高认为标签一致（算是伪标签），通过最大化互信息下界的损失函数，来指导模型训练；　
• Multi-Task Self-Supervised Learning
  • 本文工作可以被认为是这种类型；
• Automated Loss Function Search
  • 无基于无监督条件下，损失函数组合的设计并没有被过多的研究；

3 Method

　　该节将介绍本文提出的框架：automated self-supervised task search（AutoSSL）。

　　给定一个图 $\mathcal{G}$，一个 GNN 编码器 $f_{\theta}(\cdot)$ 和一组 $n$个自监督损失$ \left\{\ell_{1}, \ell_{2}, \ldots, \ell_{n}\right\} $，我们的目标是学习一组损失权重 $\left\{\lambda_{1}, \lambda_{2}, \ldots, \lambda_{n}\right\} $，这样使用加权损失组合 $\sum_{i=1}^{n} \lambda_{i} \ell_{i}$ 训练的 $f_{\theta}(\cdot)$ 可以从给定的图数据中提取有意义的特征。关键的挑战是如何从数学上定义“有意义的特征”。如果我们可以访问下游任务的标签，我们就可以将“有意义的特性”定义为可以在给定的下游任务上具有高性能的特性（节点嵌入）。然后，我们可以简单地采用下游性能作为优化目标，并将自动自监督任务搜索的问题表述如下：

　　　　$\underset{\lambda_{1}, \cdots, \lambda_{n}}{\text{min}}\mathcal{H}\left(f_{\theta^{*}}(\mathcal{G})\right), \quad\quad \text { s.t. } \theta^{*}=\arg \underset{\theta}{\text{min}} \mathcal{L}\left(f_{\theta},\left\{\lambda_{i}\right\},\left\{\ell_{i}\right\}\right)=\arg \underset{\theta}{\text{min}} \sum\limits _{i=1}^{n} \lambda_{i} \ell_{i}\left(f_{\theta}(\mathcal{G})\right) \quad\quad\quad(1)$

　　其中，$\mathcal{H}$  表示所获得的节点嵌入的质量度量，它可以是任何评估下游性能的度量，如节点分类任务的交叉熵损失。然而，在自监督设置下，我们无法访问标记数据，因此不能使用下游性能来衡量嵌入质量。相反，我们需要一个无监督的质量度量 $\mathcal{H}$  来评估所获得的嵌入的质量。简而言之，自动化自监督学习的一个挑战是：如何在不访问下游任务的标签信息的情况下构建自动化任务搜索的目标。

3.1 Pseudo-homophily

　　Definition 1 (Homophily). The homophily of a graph $G$ with node label vector $y$ is given by

　　　　$h(\mathcal{G}, y)=\frac{1}{|\mathcal{E}|} \sum\limits _{\left(v_{1}, v_{2}\right) \in \mathcal{E}} \mathbb{1}\left(y_{v_{1}}=y_{v_{2}}\right)\quad\quad\quad(2)$

　　where $y_{v_{i}}$  indicates node $v_{i} $ 's label and $\mathbb{1}(\cdot) $ is the indicator function. 

　　不同数据集同质性计算：

　　

　　如前所述，在 SSL 的任务中，真实标签是不可用的。基于 DeepCluster(Caronetal.，2018)，我们使用学习特征的聚类分配作为伪标签来训练神经网络，我们建议基于聚类分配来计算同质性，我们称之为伪同质性（pseudo-homophily）。具体来说，首先对得到的节点嵌入进行 $\text{k-means}$ 聚类，得到 $k$ 个聚类。然后将聚类结果作为伪标签，基于$\text{Eq.2}$进行同质性计算 。

理论分析

　　在这项工作中，我们提出通过最大化伪同质性来实现自我监督的任务搜索。为了理解它的合理性，我们发展了以下定理来证明伪同质性最大化与伪标签与真实标签之间的互信息的上界有关。

　　Theorem 1：给定一张图 $\mathcal{G}=\{\mathcal{V}, \mathcal{E}\}$，一个伪标签向量 $A \in   \{0,1\}^{N}$ ，一个真实标签向量 $B \in\{0,1\}^{N} $ ，我们定义 $A$ 和 $B$ 在 $\mathcal{G}$ 上的同质性分别为 $h_{A}$ 和 $h_{B}$ 。如果 $A$ 和 $B$ 中的类分布是平衡的且 $h_{A}<h_{B}$ ，那么有 

　　1、$A$ 和 $B$ 之间的互信息 $M I(A, B) $ 拥有上界 $\mathcal{U}_{A, B}$ ，且

　　　　    $\mathcal{U}_{A, B}=\frac{1}{N}\left[2 \Delta \log \left(\frac{4}{N} \Delta\right)+2\left(\frac{N}{2}-\Delta\right) \log \left(\frac{4}{N}\left(\frac{N}{2}-\Delta\right)\right)\right]$ 

　　      其中：$\Delta=\frac{\left(h_{B}-h_{A}\right)|\mathcal{E}|}{2 d_{\max }} $ ，$d_{\max }$ 表示图中最大的节点度。

　　2、如果 $h_{A}<h_{A^{\prime}}<h_{B}$，我们有 $\mathcal{U}_{A, B}<\mathcal{U}_{A^{\prime}, B} $

　　上述定理表明，伪同质性和真实同质性之间的差异越大，伪标签和真实标签之间的互信息的上界就越小。因此，由于我们假设图的伪同质性很高，所以最大化伪伪同质性就是最大化伪标签和真实标签之间的互信息的上界。

3.2 Search algorithms

　　上一节分析了最大化伪同质性的重要性，因此对于 $\text{Eq.1}$ 的优化问题，可以简单地将 $\mathcal{H}$ 设置为负的伪同质性（negative pseudo-homophily），但是，对特定任务组合的评估涉及到模型的拟合和伪同配性的评估，这花销是非常昂贵的。因此，SSL task 任务搜索的另一个挑战是如何设计一个高效的算法。接下来，详细介绍了本文设计的两种搜索策略，即 AUTOSSL-ES 和 AUTOSSL-DS。

3.2.1 AutoSSL-ES：Evolutionary strategy

　　Evolution 算法由于其设计的并行性，经常用于自动机器学习，如超参数调优。本文使用了协方差矩阵自适应进化策略（covariance matrix adaptation evolution strategy，CMA-ES)，这是 state-of-theart 的连续黑盒函数优化器，用来优化组合的自监督损失。本文将这种 SSL 任务搜索方法命名为AutoSSL-ES。

　　在 CMA-ES 的每次迭代中，它从多元正态分布中抽取一组候选解（即任务权值 $\left\{\lambda_{i}\right\}$），并在组合损失函数下训练 GNN 编码器。

• • 在 CMA-ES 的每次迭代中，它从多元正态分布中抽取一组候选解(即任务权值 $\left\{\lambda_{i}\right\}$)，并在组合损失函数下训练 GNN 编码器；
  • 然后由 $\mathcal{H}$ 评估来自训练编码器的嵌入；
  • 基于 $\mathcal{H}$ ，CMA-ES调整正态分布，以给予可能产生较低 $\mathcal{H}$ 值的样本更高的概率；

3.2.2 AutoSSL-DS:Differentiable search meta-gradient descent

　　虽然上述 AutoSSL-ES 是可并行的，但搜索成本仍然昂贵，因为它需要评估大量的候选组合，其中每个评估都涉及在大型训练时期拟合模型。因此，希望开发基于梯度的搜索方法来加速搜索过程。在本小节中，我们将介绍我们提出的框架的另一种变体，AutoSSL-DS，它通过元梯度下降来执行可微搜索。然而，伪同质性是不可微的，因为它是基于 k-means 聚类的硬聚类分配。接下来，我们将首先介绍如何使聚类过程成为可微搜索，然后介绍如何执行可微搜索。

Soft Clustering

　　虽然 k-means 聚类将数据样本的 hard assignments 给聚类，但它可以看作是高斯混合模型的一种特殊情况，它基于后验概率进行软赋值。给定一个具有质心 $\left\{\mathbf{c}_{1}, \mathbf{c}_{2}, \ldots, \mathbf{c}_{k}\right\}$ 和固定方差 $\sigma^{2}$ 的高斯混合模型，我们可以计算后验概率如下：

　　　　$p\left(\mathbf{x} \mid \mathbf{c}_{i}\right)=\frac{1}{\sqrt{2 \pi \sigma^{2}}} \exp \left(-\frac{\left\|\mathbf{x}-\mathbf{c}_{i}\right\|_{2}}{2 \sigma^{2}}\right)\quad\quad\quad(3)$

　　其中，$\mathrm{x}$ 是数据样本的特征向量，考虑一个等同的先验：$p\left(\mathbf{c}_{1}\right)=p\left(\mathbf{c}_{2}\right)=\ldots=p\left(\mathbf{c}_{k}\right)$ ，可以计算特征向量 $\mathrm{x}$ 属于簇 $\mathbf{x}$ 的概率：

　　　　$p\left(\mathbf{c}_{i} \mid \mathbf{x}\right)=\frac{p\left(\mathbf{c}_{i}\right) p\left(\mathbf{x} \mid \mathbf{c}_{i}\right)}{\sum\limits _{j}^{k} p\left(\mathbf{c}_{j}\right) p\left(\mathbf{x} \mid \mathbf{c}_{j}\right)}=\frac{\exp -\frac{\left(\mathbf{x}-\mathbf{c}_{i}\right)^{2}}{2 \sigma^{2}}}{\sum\limits_{j=1}^{k} \exp -\frac{\left(\mathbf{x}-\mathbf{c}_{j}\right)^{2}}{2 \sigma^{2}}}\quad\quad\quad(4)$

　　当  $\sigma \rightarrow 0$  ，可以获得如同  $k -means$ 的 hard assignments。计算特征向量属于某个簇的概率就简化成了计算它们之间的距离。因此可以构建同质性 loss function：

　　　　$\mathcal{H}\left(f_{\theta^{*}}(\mathcal{G})\right)=\frac{1}{k|\mathcal{E}|} \sum\limits _{i=1}^{k} \sum\limits_{\left(v_{1}, v_{2}\right) \in \mathcal{E}} \ell\left(p\left(\mathbf{c}_{i} \mid \mathbf{x}_{v_{1}}\right), p\left(\mathbf{c}_{i} \mid \mathbf{x}_{v_{2}}\right)\right)\quad\quad\quad(5)$

　　$\ell $ 用于度量两个输入之间的差异，也就是在计算图中相邻的节点之间的标签分布差异，这是一个 soft assignments，因此可以计算  $\mathcal{H}$  相对于编码器参数  $\theta$  的梯度。

　　算法如下：

　　

Search via Meta Gradient Descent

　　　　$\underset{\lambda_{1}, \cdots, \lambda_{n}}{\text{min}}\mathcal{H}\left(f_{\theta^{*}}(\mathcal{G})\right), \quad\quad \text { s.t. } \theta^{*}=\arg \underset{\theta}{\text{min}} \mathcal{L}\left(f_{\theta},\left\{\lambda_{i}\right\},\left\{\ell_{i}\right\}\right)=\arg \underset{\theta}{\text{min}} \sum\limits _{i=1}^{n} \lambda_{i} \ell_{i}\left(f_{\theta}(\mathcal{G})\right) \quad\quad\quad(1)$

　　这个优化问题是二层决策（bilevel）问题，求解的一般方式是通过梯度下降算法交替地优化内部和外部问题。然而，由于$\mathcal{H}$与  ${\lambda_i}$ 没有直接关系，不能对 $\text{Eq.1}$ 中的外部问题进行梯度下降。这个问题可以使用元梯度，即梯度相对于超参数，它在解决元学习中的 bilevel 问题中得到了广泛的应用。为了获得元梯度，需要通过神经网络的学习阶段进行反向传播。具体地说，$\mathcal{H}$相对于 ${\lambda_i}$ 的元梯度为：

　　　　$\nabla_{\left\{\lambda_{i}\right\}}^{\text {meta }}:=\nabla_{\left\{\lambda_{i}\right\}} \mathcal{H}\left(f_{\theta^{*}}(G)\right) \quad \text { s.t. } \theta^{*}=\operatorname{opt}_{\theta}\left(\mathcal{L}\left(f_{\theta},\left\{\lambda_{i}, \ell_{i}\right\}\right)\right)\quad\quad\quad(6)$

　　其中，$opt_{\theta }$ 表示内部获得 $\theta^{*}$ 的优化函数，通常是多步梯度下降。如将 $opt_{\theta }$ 视为 $T+1$ 步的梯度下降，学习率为$\epsilon$：

　　　　$\theta_{t+1}=\theta_{t}-\epsilon \nabla_{\theta_{t}} \mathcal{L}\left(f_{\theta_{t}},\left\{\lambda_{i}, \ell_{i}\right\}\right)\quad\quad\quad(7)$

　　通过展开训练过程，可以将元梯度表示为

　　　　$\nabla_{\left\{\lambda_{i}\right\}}^{\text {meta }}:=\nabla_{\left\{\lambda_{i}\right\}} \mathcal{H}\left(f_{\theta_{T}}(G)\right)=\nabla_{f_{\theta_{T}}} \mathcal{H}\left(f_{\theta_{T}}(G)\right) \cdot\left[\nabla_{\left\{\lambda_{i}\right\}} f_{\theta_{T}}(G)+\nabla_{\theta_{T}} f_{\theta_{T}}(G) \nabla_{\left\{\lambda_{i}\right\}} \theta_{T}\right]\quad\quad\quad(8)$

　　其中， 

　　　　$\nabla_{\left\{\lambda_{i}\right\}} \theta_{T}=\nabla_{\left\{\lambda_{i}\right\}} \theta_{T-1}-\epsilon \nabla_{\left\{\lambda_{i}\right\}} \nabla_{\theta_{T-1}} \mathcal{L}\left(f_{\theta_{T-1}},\left\{\lambda_{i}, \ell_{i}\right\}\right)$

　　由于 $\nabla_{\left\{\lambda_{i}\right\}} f_{\theta_{T}}(G)=0$，因此：

　　　　$\nabla_{\left\{\lambda_{i}\right\}}^{\text {meta }}:=\nabla_{\left\{\lambda_{i}\right\}} \mathcal{H}\left(f_{\theta_{T}}(G)\right)=\nabla_{f_{\theta_{T}}} \mathcal{H}\left(f_{\theta_{T}}(G)\right) \cdot \nabla_{\theta_{T}} f_{\theta_{T}}(G) \nabla_{\left\{\lambda_{i}\right\}} \theta_{T}\quad\quad\quad(9)$

　　由 $\text{Eq.7}$，$\theta_{T-1}$  也取决于权重  $\left\{\lambda_{i}\right\}$  ，因此对权重的偏导链将会追溯到  $\theta_{0}$  ，通过展开所有的内部优化步骤，获得了元梯度  $\nabla_{\left\{\lambda_{i}\right\}}^{\mathrm{meta}}$  ，使用这个实现了 $ \left\{\lambda_{i}\right\}$  的梯度下降优化:

　　算法如下：

　　

4 Experiment

　　Q1：与训练个体SSL任务相比，AutoSSL 能否获得更好的性能？
　　Q2：与 AutoSSL 相比，其他无监督节点表示学习基线和有监督节点表示学习基线如何？
　　Q3：我们能否观察到 AutoSSL 的伪同质性目标与下游分类性能之间的关系？
　　Q4：在自动训练过程中，SSL任务的权重、伪同质性目标和下游性能如何演变？

4.1 performance comparison with individual tasks

　　

4.2 Performance comparison with supervised and unsupervised baselines 

　　

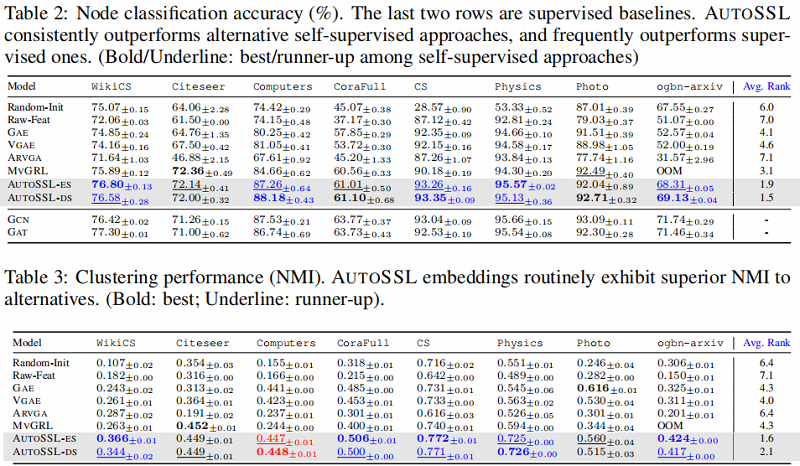
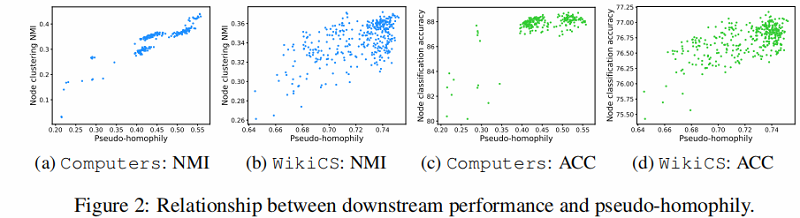
4.3 Relation between downstream performance and pseudo-homophily

　　

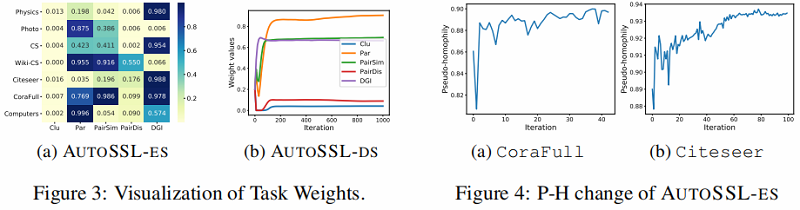
4.4 Evolution of SSL task weights ,pseudo-homophily and performance

　　

5 Conclusion 

　　图自监督学习在学习表达性节点/图表示方面取得了巨大的成功。然而，在这项工作中，我们发现为图设计的SSL任务在不同的数据集和下游任务上的表现有所不同。因此，组合多个SSL任务来联合编码多个信息源并产生更一般化的表示是值得的。然而，在没有访问标记数据的情况下，它给测量SSL任务组合的质量带来了巨大的挑战。为了解决这个问题，我们利用图的同质性，提出伪同质性来衡量SSL任务组合的质量。然后我们从理论上证明了最大化伪同质性有助于最大化伪标签和地面真标签之间互信息的上界。在伪同质性测度的基础上，我们开发了两种自动框架和自动-ds来有效地搜索任务权值。大量的实验表明，autossl能够通过组合各种SSL任务来产生更泛化的表示。

 

高斯混合模型  

 https://blog.csdn.net/weixin_39478524/article/details/109368216

 https://zhuanlan.zhihu.com/p/81255623