论文解读(MLGCL)《Multi-Level Graph Contrastive Learning》
论文信息
论文标题:Multi-Level Graph Contrastive Learning
论文作者:Pengpeng Shao, Tong Liu, Dawei Zhang, J. Tao, Feihu Che, Guohua Yang
论文来源:2021, Neurocomputing
论文地址:download
论文代码:download
1 Introduction
本文贡献:
-
- 提出多层次图对比学习框架:联合节点级和图级对比学习;
- 引入 KNN 图提取语义信息;
本文开发了一个多层次的图对比学习(MLGCL)框架,用于通过对比图的拓扑视图和特征空间视图来学习图数据的鲁棒表示。如 Figure 2 所示,使用 KNN 算法对特征进行编码,从而在特征空间中生成 KNN 视图。KNN 视图不仅提供了互补视图,而且更适合GNN,将两者对比学习结合,可以显著提高 GNN 编码器的鲁棒性和适应性。
2 Method
整体框架:
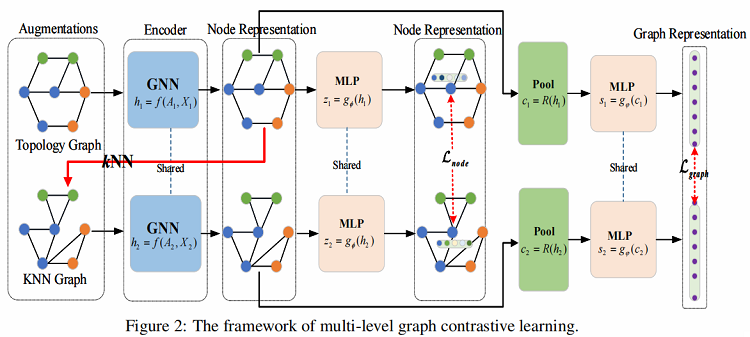
框架流程
-
- 步骤一:从增强池 $\tau $ 中采样一对图增强函数 ${\tau }_{1}$ 和 ${\tau }_{2}$,并将其应用于输入图,生成两个视图的增广图;
- 步骤二:使用一对共享的 GNN 编码器来提取节点表示,并进一步利用池化层来提取图表示;
- 步骤三:利用一个共享参数的 MLP 层来将两个视图中的节点表示投影到计算节点级对比损失的空间中。类似地,还将来自两个视图的图表示投影到计算图级对比损失的空间中;
- 步骤四:通过优化所提出的多级损失函数来学习编码器的参数;
2.1 KNN graph
给定 $G(A、X)$ 的图结构,先利用 GNN 编码器提取拓扑图的编码特征 $Z$,然后利用 $\text{KNN}$ 对 $Z$ 的近邻构造 $\text{KNN}$ 图($G_{f}\left(A_{f}, X\right)$),其中 $A_{f}$ 为 $\text{KNN}$ 图的邻接矩阵。
构建 $\text{KNN}$ 图可以描述为两个步骤:
-
- 首先,基于 $ N$ 个编码特征 $ Z $ 计算相似度矩阵 $S$;
- 其次,为每个节点选择前 $k$ 个相似的节点对来设置边,最后得到 $\text{KNN}$ 图的邻接矩阵 $A_{f} $ ;
相似性计算常用方法:
- 马氏距离
$S_{i j}=\sqrt{\left(x_{i}-x_{j}\right)^{T} M\left(x_{i}-x_{j}\right)}$
其中 $M$ 是一个正半定矩阵,它起着逆协方差矩阵的作用。 (如果 $M$ 是单位矩阵,则为欧氏距离)
正半定矩阵:设 $A$ 是 $n$ 阶方阵,如果对任何非零向量 $X$,都有 $X ' A X \geq 0$ ,其中 $X ' $ 表示 $X$ 的转置,就称 $A$ 为半正定矩阵。
- 余弦相似性
使用两个向量之间夹角的余弦值来度量相似性:
${\large S_{i j}=\frac{x_{i} \cdot x_{j}}{\left|x_{i}\right|\left|x_{j}\right|}} $
- 高斯核
${\large S_{i j}=e^{-\frac{\left\|x_{i}-x_{j}\right\|^{2}}{2 \sigma^{2}}}} $
其中, $\sigma$ 是高斯核的核宽度。
本文选择余弦相似性来得到相似性矩阵 $S$ 。
2.2 Encoder and Readout
Encoder 使用双层 GCN 获得节点表示:
$Z^{l+1}=f(A, X)=\sigma\left(\widetilde{A} Z^{l} W^{l}\right)$
其中:$\widetilde{A}=\widehat{D}^{-1 / 2} \widehat{A} \widehat{D}{ }^{-1 / 2}$ 是对称归一化的邻接矩阵。
对于每个视图的节点表示 $Z_{a} $, $Z_{b} $ ,使用一个图池化层 $ P(\cdot): \mathbb{R}^{N \times d} \rightarrow \mathbb{R}^{d}$ (即读出函数),得到图表示:
$c=P(H)=\sigma\left(\frac{1}{N} \sum_{i=1}^{N} h_{i}\right)$
此外,为了对两个视图进行相应的节点表示和图表示对比,使用 MLP 层 $g_{\phi}(\cdot) 和 g_{\varphi}(\cdot): \mathbb{R}^{N \times d} \rightarrow \mathbb{R}^{N \times d}$ 将节点和图表示分别投影到计算对比损失的空间中。
2.3 Loss function
多级损失函数,由两部分组成:两个视图之间低级节点表示的对比,以及两个视图之间高级图表示的对比。
低级节点表示的对比:给定正对 $(z_i、z_j)$,将节点级对比损失函数定义为
${\large \mathcal{L}_{\text {node }}\left(z_{i}^{a}, z_{i}^{b}\right)=\log \frac{\exp \left(\left(z_{i}^{a}\right)^{T} z_{i}^{b} / \tau\right)}{\sum_{j=1, j \neq i}^{K} \exp \left(\left(z_{i}^{a}\right)^{T} z_{i}^{b} / \tau\right)+\exp \left(\left(z_{i}^{a}\right)^{T} z_{j}^{a} / \tau\right)+\exp \left(\left(z_{i}^{a}\right)^{T} z_{j}^{b} / \tau\right)}} $
由于两个视图是对称的,所以另一个视图的损失被定义为 $L_{n o d e}\left(z_{i}^{b}, z_{i}^{a}\right)$ 。因此,通过优化以下内容,实现最大化两个视图之间的节点的一致性:
$\mathcal{L}_{n o d e}=\mathcal{L}_{n o d e}\left(z_{i}^{a}, z_{i}^{b}\right)+\mathcal{L}_{n o d e}\left(z_{i}^{b}, z_{i}^{a}\right)$
高级图表示的对比:给定正例 $\left(s^{a}, s^{b}\right)$ 和负例 $\left(s^{a}, \tilde{s}^{a}\right)$ ,$\left(s^{a}, \tilde{s}^{b}\right)$ ,两个视图之间的图表示对比被定义为:
${\large \mathcal{L}_{\text {graph }}\left(s^{a}, s^{b}\right)=\log \frac{\exp \left(\left(s^{a}\right)^{T} s^{b} / \tau\right)}{\exp \left(\left(s^{a}\right)^{T} s^{b} / \tau\right)+\exp \left(\left(s^{a}\right)^{T} \tilde{s}^{a} / \tau\right)+\exp \left(\left(s^{a}\right)^{T} \tilde{s}^{b} / \tau\right)}} $
本文为生成图的负样本,随机 shuffle 特征以推导出负邻接矩阵 $\widetilde{A}$ 和 $\widetilde{A}_{f}$ ,然后得到负样本 $\left(s^{a}, \tilde{s}^{a}\right) ,\left(s^{a}, \tilde{s}^{b}\right) $ 。由于对称性,另一个视图的损失被定义为 $L_{g r a p h}\left(s^{b}, s^{a}\right) $ 。因此,整体图表示对比为:
$\mathcal{L}_{g r a p h}=\mathcal{L}_{g r a p h}\left(s^{a}, s^{b}\right)+\mathcal{L}_{g r a p h}\left(s^{b}, s^{a}\right)$
最后,通过将节点级对比损失与图级对比损失相结合,模型的多级损失为:
$\mathcal{L}=\mathcal{L}_{\text {node }}+\lambda \mathcal{L}_{\text {graph }}$
3 Experiment
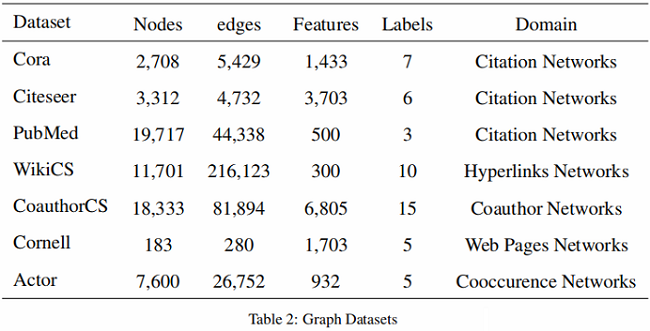
数据集
节点分类


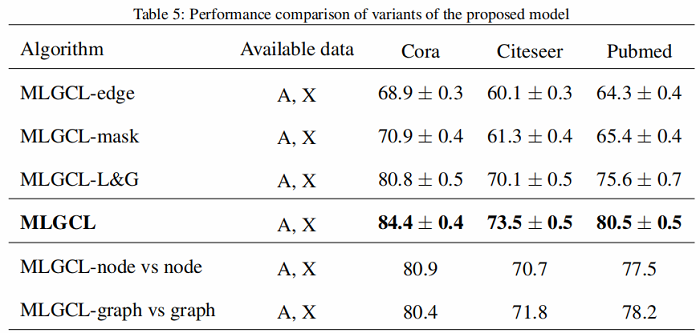
4 Conclusion
-
- 提出多层次图对比学习框架:联合节点级和图级对比学习;
- 引入 $\text{KNN}$ 图提取语义信息;
因上求缘,果上努力~~~~ 作者:图神经网络,转载请注明原文链接:https://www.cnblogs.com/BlairGrowing/p/16124243.html


