论文解读（GRACE）《Deep Graph Contrastive Representation Learning》

论文解读

论文标题：Deep Graph Contrastive Representation Learning
论文作者：Yanqiao Zhu, Yichen Xu, Feng Yu, Q. Liu, Shu Wu, Liang Wang
论文来源：2020, ArXiv
论文地址：download 
代码地址：download (代码写的不错)

1 Introduction

　　节点级图对比学习框架。

　　数据增强：边删除、特征隐藏。

2 Method

　　GRACE 框架如下：

　　

class Encoder(torch.nn.Module):
    def __init__(self, in_channels: int, out_channels: int, activation,
                 base_model=GCNConv, k: int = 2):
        super(Encoder, self).__init__()
        self.base_model = base_model

        assert k >= 2
        self.k = k
        self.conv = [base_model(in_channels, 2 * out_channels)]
        for _ in range(1, k-1):
            self.conv.append(base_model(2 * out_channels, 2 * out_channels))
        self.conv.append(base_model(2 * out_channels, out_channels))
        self.conv = nn.ModuleList(self.conv)

        self.activation = activation

    def forward(self, x: torch.Tensor, edge_index: torch.Tensor):
        for i in range(self.k):
            x = self.activation(self.conv[i](x, edge_index))
        return x


class Model(torch.nn.Module):
    def __init__(self, encoder: Encoder, num_hidden: int, num_proj_hidden: int,
                 tau: float = 0.5):
        super(Model, self).__init__()
        self.encoder: Encoder = encoder
        self.tau: float = tau

        self.fc1 = torch.nn.Linear(num_hidden, num_proj_hidden)
        self.fc2 = torch.nn.Linear(num_proj_hidden, num_hidden)

    def forward(self, x: torch.Tensor,
                edge_index: torch.Tensor) -> torch.Tensor:
        return self.encoder(x, edge_index)

    def projection(self, z: torch.Tensor) -> torch.Tensor:
        z = F.elu(self.fc1(z))
        return self.fc2(z)

    def sim(self, z1: torch.Tensor, z2: torch.Tensor):
        z1 = F.normalize(z1)
        z2 = F.normalize(z2)
        return torch.mm(z1, z2.t())

    def semi_loss(self, z1: torch.Tensor, z2: torch.Tensor):
        f = lambda x: torch.exp(x / self.tau)
        refl_sim = f(self.sim(z1, z1))
        between_sim = f(self.sim(z1, z2))

        return -torch.log(
            between_sim.diag()
            / (refl_sim.sum(1) + between_sim.sum(1) - refl_sim.diag()))

    def batched_semi_loss(self, z1: torch.Tensor, z2: torch.Tensor,
                          batch_size: int):
        # Space complexity: O(BN) (semi_loss: O(N^2))
        device = z1.device
        num_nodes = z1.size(0)
        num_batches = (num_nodes - 1) // batch_size + 1
        f = lambda x: torch.exp(x / self.tau)
        indices = torch.arange(0, num_nodes).to(device)
        losses = []

        for i in range(num_batches):
            mask = indices[i * batch_size:(i + 1) * batch_size]
            refl_sim = f(self.sim(z1[mask], z1))  # [B, N]
            between_sim = f(self.sim(z1[mask], z2))  # [B, N]

            losses.append(-torch.log(
                between_sim[:, i * batch_size:(i + 1) * batch_size].diag()
                / (refl_sim.sum(1) + between_sim.sum(1)
                   - refl_sim[:, i * batch_size:(i + 1) * batch_size].diag())))

        return torch.cat(losses)

    def loss(self, z1: torch.Tensor, z2: torch.Tensor,
             mean: bool = True, batch_size: int = 0):
        h1 = self.projection(z1)
        h2 = self.projection(z2)

        if batch_size == 0:
            l1 = self.semi_loss(h1, h2)
            l2 = self.semi_loss(h2, h1)
        else:
            l1 = self.batched_semi_loss(h1, h2, batch_size)
            l2 = self.batched_semi_loss(h2, h1, batch_size)

        ret = (l1 + l2) * 0.5
        ret = ret.mean() if mean else ret.sum()

        return ret

2.1 The Contrastive Learning Framework

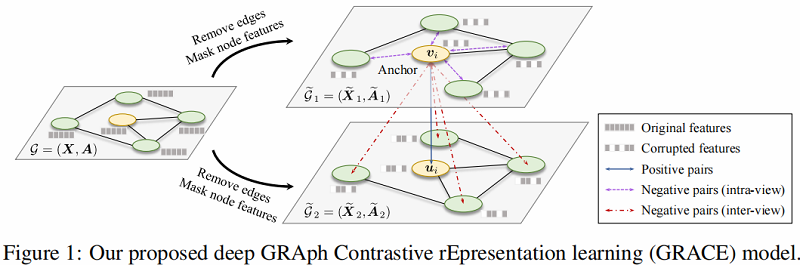
　　首先，通过随机破坏原始图来生成两个视图，分别为  $G_{1}$  和  $G_{2}$ 。

　　其次，通过 Encoder 获得节点表示， 分别为 $U=f\left(\widetilde{\boldsymbol{X}}_{1}, \widetilde{\boldsymbol{A}}_{1}\right) $ 和  $V=f\left(\widetilde{\boldsymbol{X}}_{2}, \widetilde{\boldsymbol{A}}_{2}\right) $ 。

　　对比目标：采用视图之间的节点一致性，即：对于任何节点  $v_{i}$，它在一 个视图中生成的嵌入  $\boldsymbol{u}_{i}$  被视为锚嵌入，在另一个视图中 $v_{i}$ 生成的节点嵌入 $\boldsymbol{v}_{i}$ 为正样本，在两个视图中除  $v_{i}$  以外的节点表示被视为负样本。

　　每个正对 $\left(\boldsymbol{u}_{i}, \boldsymbol{v}_{i}\right)$  的对目标定义为：

　　　　${\large \ell\left(\boldsymbol{u}_{i}, \boldsymbol{v}_{i}\right)=-\log \frac{e^{\theta\left(\boldsymbol{u}_{i}, \boldsymbol{v}_{i}\right) / \tau}}{\underbrace{e^{\theta\left(\boldsymbol{u}_{i}, \boldsymbol{v}_{i}\right) / \tau}}_{\text {the positive pair }}+\underbrace{\sum\limits_{k=1}^{N} \mathbb{1}_{[k \neq i]} e^{\theta\left(\boldsymbol{u}_{i}, \boldsymbol{v}_{k}\right) / \tau}}_{\text {inter-view negative pairs }}+\underbrace{\sum\limits_{k=1}^{N} \mathbb{1}_{[k \neq i]} e^{\theta\left(\boldsymbol{u}_{i}, \boldsymbol{u}_{k}\right) / \tau}}_{\text {intra-view negative pairs }}}} \quad\quad\quad\quad(1)$

　　其中 ，$\theta(\boldsymbol{u}, \boldsymbol{v})=s(g(\boldsymbol{u}), g(\boldsymbol{v})) $ 代表余弦相似度距离。

　　因此，总体目标函数为：

　　　　$\mathcal{J}=\frac{1}{2 N} \sum\limits _{i=1}^{N}\left[\ell\left(\boldsymbol{u}_{i}, \boldsymbol{v}_{i}\right)+\ell\left(\boldsymbol{v}_{i}, \boldsymbol{u}_{i}\right)\right]\quad\quad\quad\quad(2)$

    def loss(self, z1: torch.Tensor, z2: torch.Tensor,mean: bool = True, batch_size: int = 0):
        h1 = self.projection(z1)
        h2 = self.projection(z2)

        if batch_size == 0:
            l1 = self.semi_loss(h1, h2)
            l2 = self.semi_loss(h2, h1)
        else:
            l1 = self.batched_semi_loss(h1, h2, batch_size)
            l2 = self.batched_semi_loss(h2, h1, batch_size)

        ret = (l1 + l2) * 0.5
        ret = ret.mean() if mean else ret.sum()

        return ret

    def semi_loss(self, z1: torch.Tensor, z2: torch.Tensor):
        f = lambda x: torch.exp(x / self.tau)
        refl_sim = f(self.sim(z1, z1))
        between_sim = f(self.sim(z1, z2))

        return -torch.log(
            between_sim.diag()/ (refl_sim.sum(1) + between_sim.sum(1) - refl_sim.diag())
        )


    def batched_semi_loss(self, z1: torch.Tensor, z2: torch.Tensor,
                          batch_size: int):
        # Space complexity: O(BN) (semi_loss: O(N^2))
        device = z1.device
        num_nodes = z1.size(0)
        num_batches = (num_nodes - 1) // batch_size + 1
        f = lambda x: torch.exp(x / self.tau)
        indices = torch.arange(0, num_nodes).to(device)
        losses = []

        for i in range(num_batches):
            mask = indices[i * batch_size:(i + 1) * batch_size]
            refl_sim = f(self.sim(z1[mask], z1))  # [B, N]
            between_sim = f(self.sim(z1[mask], z2))  # [B, N]

            losses.append(-torch.log(
                between_sim[:, i * batch_size:(i + 1) * batch_size].diag()
                / (refl_sim.sum(1) + between_sim.sum(1)
                   - refl_sim[:, i * batch_size:(i + 1) * batch_size].diag())))

        return torch.cat(losses)

　　GRACE 算法流程：

　　

2.2 Graph View Generation

2.2.1 Removing edges (RE)

　　首先采样一个随机掩蔽矩阵 $\widetilde{\boldsymbol{R}} \in\{0,1\}^{N \times N}$，矩阵中每个元素依据伯努利分布生成。如果 $\boldsymbol{A}_{i j}=1$ ，则它的值来自伯努利分布 $\widetilde{\boldsymbol{R}}_{i j} \sim \mathcal{B}\left(1-p_{r}\right) $ ，否则 $\widetilde{\boldsymbol{R}}_{i j}=0 $ 。这里的 $p_{r}$ 是每条边被删除的概率。所得到的邻接矩阵可以计算为

　　　　$\widetilde{\boldsymbol{A}}=\boldsymbol{A} \circ \widetilde{\boldsymbol{R}}\quad\quad\quad(3)$

　　其中：$(\boldsymbol{x} \circ \boldsymbol{y})_{i}=x_{i} y_{i}$ 代表着 Hadamard product 。

edge_index_1 = dropout_adj(edge_index, p=drop_edge_rate_1)[0]
edge_index_2 = dropout_adj(edge_index, p=drop_edge_rate_2)[0]

2.2.2 Masking node features (MF)

　　首先对随机向量  $\widetilde{m} \in\{0,1\}^{F}$  进行采样，其中它的每个维度值都独立地从概率为  $1-p_{m}$  的伯努利分布中提取，即  $\widetilde{m}_{i} \sim   \mathcal{B}\left(1-p_{m}\right) $ 。然后，生成的节点特征  $\widetilde{\boldsymbol{X}}$  为:

　　　　$\tilde{\boldsymbol{X}}=\left[\boldsymbol{x}_{1} \circ \widetilde{\boldsymbol{m}} ; \boldsymbol{x}_{2} \circ \widetilde{\boldsymbol{m}} ; \cdots ; \boldsymbol{x}_{N} \circ \widetilde{\boldsymbol{m}}\right]^{\top}\quad\quad\quad\quad(4)$

　　其中：$[\cdot ;]$ 代表着拼接操作。

def drop_feature(x, drop_prob):
    drop_mask = torch.empty(
        (x.size(1), ),
        dtype=torch.float32,
        device=x.device).uniform_(0, 1) < drop_prob
    x = x.clone()
    x[:, drop_mask] = 0

    return x

　　本文共同利用这两种方法来生成视图。  $\tilde{\mathcal{G}}_{1}$  和  $\widetilde{\mathcal{G}}_{2}$  的生成由两个超参数  $p_{r}$  和  $p_{m}$  控制。为了在这两个视图中提供不同的上下文，这两个视图的生成过程使用了两组不同的超参数  $p_{r, 1}$ 、 $p_{m, 1}$  和  $p_{r, 2}$ 、$ p_{m, 2}$  。实验表明，我们的模型对  $p_{r}$  和  $p_{m}$  的选择不敏感，因此原始图没有过度损坏，例如，$p_{r} \leq 0.8$  和  $p_{m} \leq 0.8$  。

3 Experiments

3.1 Dataset

　　

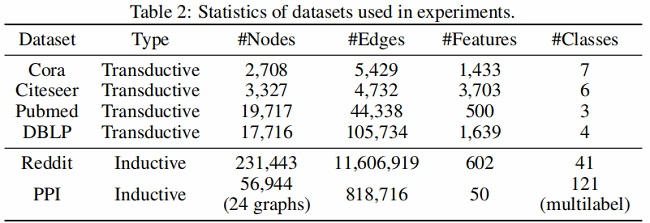
3.2 Experimental Setup

Transductive learning

　　在 Transductive learning 中，使用 $2$ 层的 GCN 作为 Encoder：

　　　　$\mathrm{GC}_{i}(\boldsymbol{X}, \boldsymbol{A}) =\sigma\left(\hat{\boldsymbol{D}}^{-\frac{1}{2}} \hat{\boldsymbol{A}} \hat{\boldsymbol{D}}^{-\frac{1}{2}} \boldsymbol{X} \boldsymbol{W}_{i}\right)\quad\quad\quad\quad(7)$

　　　　$f(\boldsymbol{X}, \boldsymbol{A})=\mathrm{GC}_{2}\left(\mathrm{GC}_{1}(\boldsymbol{X}, \boldsymbol{A}), \boldsymbol{A}\right)\quad\quad\quad\quad(8)$

Inductive learning on large graphs

　　考虑到 Reddit 数据的大规模，本文采用具有残差连接的三层 GraphSAGE-GCN 作为编码器，其表述为

　　　　$\widehat{\mathrm{MP}}_{i}(\boldsymbol{X}, \boldsymbol{A}) =\sigma\left(\left[\hat{\boldsymbol{D}}^{-1} \hat{\boldsymbol{A}} \boldsymbol{X} ; \boldsymbol{X}\right] \boldsymbol{W}_{i}\right) \quad\quad\quad\quad(9)$

　　　　$f(\boldsymbol{X}, \boldsymbol{A}) =\widehat{\mathrm{MP}}_{3}\left(\widehat{\mathrm{MP}}_{2}\left(\widehat{\mathrm{MP}}_{1}(\boldsymbol{X}, \boldsymbol{A}), \boldsymbol{A}\right), \boldsymbol{A}\right)\quad\quad\quad\quad(10)$

　　对与像 Reddit 一样的大规模数据集，我们应用子采样方法，首先随机选择一批节点，然后通过对节点邻居进行替换，得到以每个所选节点为中心的子图。具体来说，我们分别在 1-hop，2-hop 和 3-hop采样 30、25、20 个邻居。 

Inductive learning on multiple graphs.

　　对于多图 PPI 的归纳学习，我们叠加了三个具有跳跃连接的平均池化层，类似于 DGI 。图卷积编码器可以表示为

　　　　$\boldsymbol{H}_{1}=\widehat{\mathrm{MP}}_{1}(\boldsymbol{X}, \boldsymbol{A}) \quad\quad\quad\quad(11)$

　　　　$\boldsymbol{H}_{2}=\widehat{\mathrm{MP}}_{2}\left(\boldsymbol{X} \boldsymbol{W}_{\mathrm{skip}}+\boldsymbol{H}_{1}, \boldsymbol{A}\right)\quad\quad\quad\quad(12)$

　　　　$f(\boldsymbol{X}, \boldsymbol{A})=\boldsymbol{H}_{3} =\widehat{\mathrm{MP}}_{3}\left(\boldsymbol{X} \boldsymbol{W}_{\mathrm{skip}}^{\prime}+\boldsymbol{H}_{1}+\boldsymbol{H}_{2}, \boldsymbol{A}\right)\quad\quad\quad\quad(13)$

3.3 Results and Analysis

　　

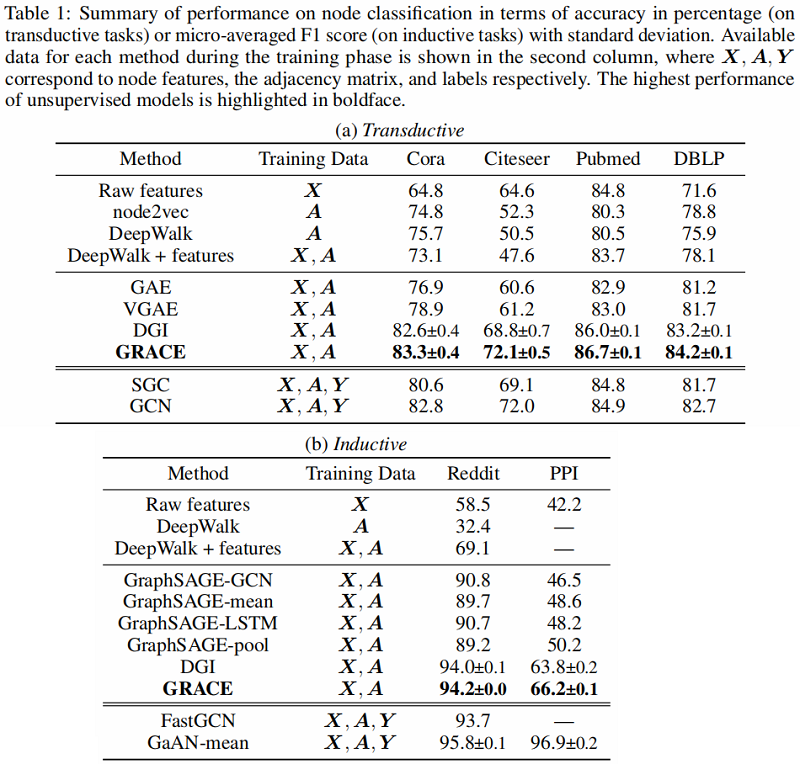
4 Conclusion

　　交叉视图节点一致性对比。

 

修改历史

2022-03-28 创建文章
2022-06-12 精读

 

论文解读目录