论文解读（Geom-GCN）《Geom-GCN: Geometric Graph Convolutional Networks》

论文信息

论文标题：Geom-GCN: Geometric Graph Convolutional Networks
论文作者：Hongbin Pei, Bingzhen Wei, K. Chang, Yu Lei, Bo Yang
论文来源：2020, ICLR
论文地址：download 
论文代码：download 

1 Intriduction

　　MPNN 存在的问题：即 丢失了节点与其邻居间的结构信息 和 无法捕获节点之间的长距离依赖关系。

　　在每一层 MPNN 中，每个节点向其邻域内的节点发送其特征表示，即一条“消息”；然后通过聚合从邻域收到的所有“消息”来更新其特征表示。

　　MPNNs 的 Aggregator 存在的问题：

　　问题一：Aggregator 丢失了节点与其邻居间的结构信息。如 GCN 单纯考虑了 一阶邻居的信息，并没有考虑邻居节点的不同，稍微好一点的工作有 GAT ，好在分配权重的观点。对于该问题采用下图做例子：

　　　　

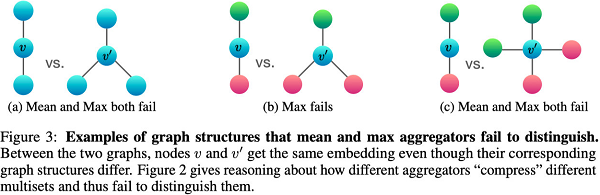
　　同构图：同构图是指图中节点类型和关系类型（边的类型）都仅有一种。
　　异构图：与同构图相反，异构图指图中节点类型或关系类型多于一种。

　　问题二：Agrgregator 缺乏捕获远距离依赖的能力。

　　可能的解决方法：使用深层的网络。实际上不可行原因，一：远距离节点无差别融合其近端节点的信息（相关和不相关的信息）。二：图中的过平滑问题：即图中节点的表示最终将趋于一样。[ 理论上是同 label 的节点表示趋于一致，当然这也是因为其无法识别同构图和异构图，将不同类别的节点视为一类 ]

　　本文解决的思路：考虑构造一个好的潜在空间，将节点映射为连续空间的一个向量（graph embedding），在隐空间查找邻居并进行聚合。

2 Geometric aggregation scheme

　　整体框架如 Fig. 1 所示：

　　　　

　　Aggregation scheme 包括三个模块：

• • Node embedding (panel A1-A3)
  • Structural neighborhood (panel B) 
  • Bi-level aggregation (panel C)

2.1. Node embedding

　　即上图中 $ A1\longrightarrow A3$ 。

　　$ A1\longrightarrow A2$ 将原始图数据映射到一个潜在空间（二维）上去，即通过映射函数 $f: v \rightarrow z_{v}$。

　　$ A2\longrightarrow A3$ 指图中局部邻域结构（或称之为局部子图），即后文所指的 $N_g(v)$。

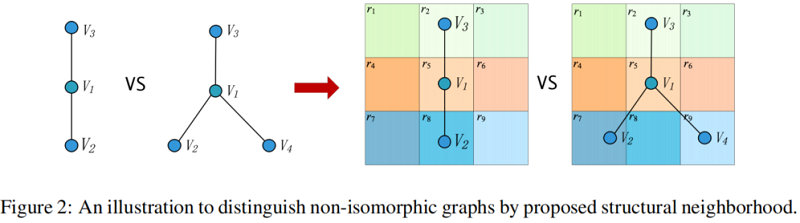
2.2 Structural neighborhood

　　即上图中 $ A3\longrightarrow B$ 。

　　$ A3\longrightarrow B$  指图中结构化邻居（Structural neighborhood），即

　　　　$\mathcal{N}(v)=\left(\left\{N_{g}(v), N_{s}(v)\right\}, \tau\right)$。

　　其中，　　

　　直接邻居 $N_{g}(v)=\{u \mid u \in V,(u, v) \in E\}$ 代表与 $v$ 相连的邻居集合  [ 即邻接矩阵中的邻居 ]。

　　潜在空间邻域 $N_{s}(v)=\left\{u \mid u \in V, d\left(\boldsymbol{z}_{u}, \boldsymbol{z}_{v}\right)<\rho\right\}$ 代表着与 $v$ 距离小于 $\rho$ 的邻居集合，即 $N_{s}(v)$ 在一定程度上包括了远距离依赖的相似邻居。

　　注意，$\rho$ 的范围从 $0$ 到 $N_{g}(v)$ 中所有节点之间的距离和的平均。

　　关系操作算子（relational operator）是一个在潜在空间中定义的函数。其输入是 $v$ 和 $u$ 的有序位置对（ordered position pair） $\left(z_{v}, z_{u}\right) $ ，该算子用于表示 $v$ 和 $u$ 的几何关系（理解为是否是邻域关系）。具体如下所示：

　　　　$\tau:\left(\boldsymbol{z}_{v}, \boldsymbol{z}_{u}\right) \rightarrow r \in R$

　　其中，$r$ 是离散值，$R$ 是几何关系的集合。对 $\tau$ 的一个要求是保证每个有序位置对有且只有一个确定的几何关系，即生成的每个 $r$ 有且只有一个 [ 方便下文中 $(i,r)$ 进行索引 ]。

　　如上面的 Fig 1. B 所示，红色的表示中心节点 $v$，蓝色节点包括与 $v$ 直接相连的节点或者与 $v$ 距离小于 $\rho $ 的节点，图中是一个 $3*3$ 的格子，每一个格子所在的节点表示与 $v$ 的一种关系。

2.3 Bi-level aggregation

　　即上图中 $ C$ 。

　　关键点： 构造虚拟节点（蓝色、绿色空心节点），即 Fig 1. C 中的 空心节点。

　　Low-level aggregation——通过聚合函数 $p$ 将相同邻域中具有相同几何关系的节点的隐藏特征聚合到虚拟节点：

　　　　$\boldsymbol{e}_{(i, r)}^{v, l+1}=p\left(\left\{\boldsymbol{h}_{u}^{l} \mid u \in N_{i}(v), \tau\left(\boldsymbol{z}_{v}, \boldsymbol{z}_{u}\right)=r\right\}\right), \forall i \in\{g, s\}, \forall r \in R \quad \text { (Low-level aggregation) }$

　　其中，$p$ 是具有平移不变性的函数，比如 $L_p$（通常 $p=1,2,\infty $）。

　　举例：

• • 绿色的虚拟节点表示  $N_{s}(v)$ （潜在空间邻居）中节点与对应的 $r$ 通过排列不变性函数 $p$ 生成的，比如 $r_4$ 中的两个节点属于 $N_{s}(v)$  中节点，并且对应一个 $r$。
  • 蓝色的虚拟节点表示  $N_{g}(v)$ (直接邻居)中节点与对应的 $r$ 通过排列不变性函数 $p$ 生成的，比如 $r_1$ 中的一个节点属于 $N_{g}(v)$  中节点，并且对应一个 $r$。而 $r_9$ 中的节点不在 $N_{g}(v)$ 中，故不生成蓝色虚拟节点。

　　High-level aggregation —— 虚拟节点的特征通过函数 $q$ 进一步聚合到中心节点：

　　　　$\boldsymbol{m}_{v}^{l+1}=\underset{i \in\{g, s\}, r \in R}{q}\left(\left(e_{(i, r)}^{v, l+1},(i, r)\right)\right)(\text{High-level aggregation})$

　　$q$ 可以考虑使用 拼接（concatenation） 来提取邻居信息。

　　Non-linear transform——使用非线性变换 $ReLU$ 得到新的表示 $\boldsymbol{h}_{v}^{(l+1)}$ ：

　　　　$\boldsymbol{h}_{v}^{l+1}=\sigma\left(W_{l} \cdot \boldsymbol{m}_{v}^{l+1}\right) $

　　本文解决一个 Aggregation 存在的一个问题，无法使用类似 mean、max 解决同质性问题。

　　

　　假设上述两张图的每个节点对应的表示均相同，那么使用 mean、max 无法识别两张图是否是一样的（图表示一样）。

　　本文的解决方法是生成虚拟节点可以采用不同的聚合函数，即 每个 $r$ 可以使用不同的聚合函数。 

2.4 Comparisons to related work

　　上文 GCN 存在的问题，以及 MPNNs 的改进工作 GAT 。

3 Geom-GCN：An implementation of the scheme

　　主要包括上述的三个模块： 

• • node embedding　　
  • structural neighborhood　　
  • aggregation function　　

3.1 Node embedding

　　获得初始节点表示采用：

• • Geom-GCN-I：Isomap　　
  • Geom-GCN-P：Poincate　　
  • Geom-GCN-S：struc2vec　　

3.2 structural neighborhood

　　对于 $N_{s}(v)$ 中的  $\rho$ 我们将其区间范围设置为从  $0$ 直到  $\operatorname{Average}\left(N_{g}(v)\right)$

3.3 aggregation function

　　本文的几何算子 $\tau$ 定义如 Table 1 所示：

　　　　

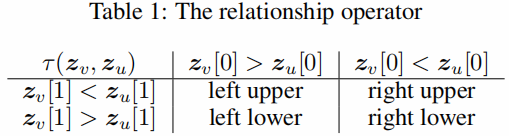
　　Low-level aggregation $p$ 其实就是 GCN 中的平均操作。

　　　　${\large \boldsymbol{e}_{(i, r)}^{v, l+1}=\sum\limits _{u \in N_{i}(v)} \delta\left(\tau\left(\boldsymbol{z}_{v}, \boldsymbol{z}_{u}\right), r\right)(\operatorname{deg}(v) \operatorname{deg}(u))^{\frac{1}{2}} \boldsymbol{h}_{u}^{l}, \forall i \in\{g, s\}, \forall r \in R} $

　　其中：

　　　　$\delta(\cdot, \cdot)$ 是一个只允许包含有关系的节点 $r$ 到 $v$ 的克罗内克增量函数

　　High-level aggregation $q$ 本质上就是 concatenation 函数，具体如下：

　　　　${\large \boldsymbol{h}_{v}^{l+1}=\sigma\left(W_{l} \cdot  \underset{i \in\{g, p\}}{||}   \underset{r \in R}{||}  \boldsymbol{e}_{(i, r)}^{v, l+1}\right)} $

4 Experiments

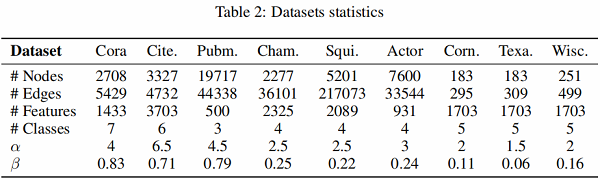
　　本文定义 $\alpha$ 作为 Gromov hyperbolicity 用来测量图的双曲率。$\alpha$ 越小，空间越双曲，这表明图所具有的层次模式越强。

　　同样使用 $\beta$ 定义节点的同质性：

　　　　$\beta=\frac{1}{N} \sum\limits _{v \in V} \frac{\text { Number of } v \text { 's neighbors who have the same label as } v}{\text { Number of } v \text { 's neighbors }} .$

　　$\beta$  值越大，说明就节点标签而言，节点对于给定图的同质性更强。

　　本文采用的数据库如 Table 2 所示：

　　　　

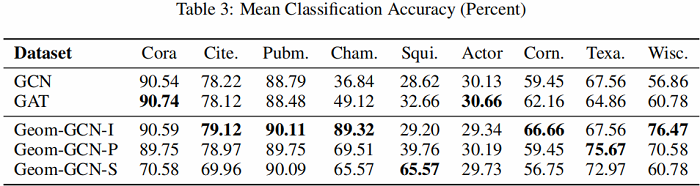
　　实验结果如 Table 3 所示：

　　　　

　　作者又进一步测试了两个变种:

• 只用原始图上邻居，加上后缀-g. 如Geom-GCN-I-g
• 只用隐空间邻居，加上后缀-s. 如Geom-GCN-I-s

　　结果见下图：

　　　　

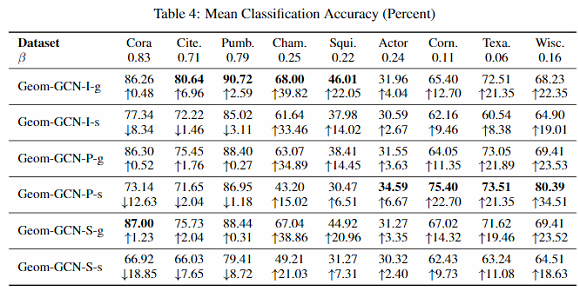
　　可以看出：隐空间邻居对 $\beta $ 较小的图贡献更大。

　　然后，作者测试了不同 embedding 方法在选取邻居上对实验结果的影响。

　　　　

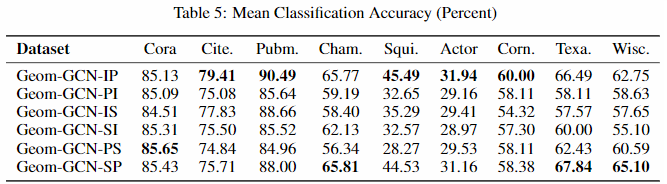
　　可以看出：这里并没有一个通用的较好embedding方法。需要根据数据集来设置，如何自动的找到最合适的embedding方法是一个future work。

　　最后是时间复杂度分析。本文考虑了多种不同的关系，因此，Geom-GCN的时间复杂度是GCN的 $|2R|$ 倍。另外，和GAT的实际运行时间相差无几，因为attention的计算通常很耗时。

　　　　

　　可视化结果：

　　　　

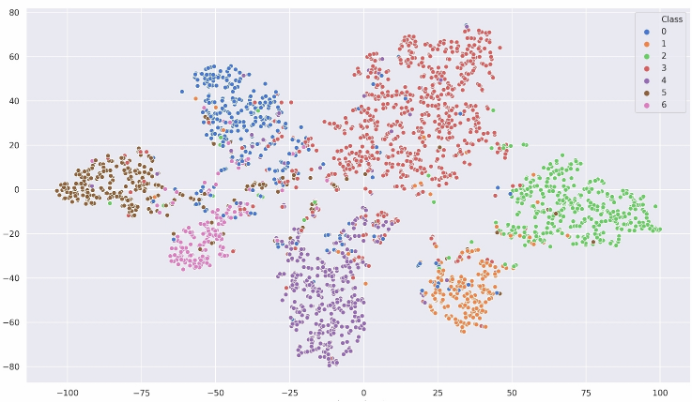
5 Conclusion and future work

　　我们解决了现有的信息传递神经网络在图上的两个主要缺点——鉴别结构的损失和长期依赖关系。作为我们的关键见解，我们通过图的嵌入将一个离散的图连接到一个连续的几何空间。也就是说，我们利用了卷积的原则：在一个有意义的空间上进行空间聚合——因此我们的方法从图中提取或“恢复”嵌入空间中丢失的信息（区分结构和长期依赖关系）。我们提出了一个通用的几何聚合方案，并用几个特定的Geom-GCN实现实例化了它，我们的实验验证了它的明显优势。作为未来的工作，我们将探索选择正确的嵌入方法的技术——不仅依赖于输入图，还依赖于目标应用程序。

 

修改历史

2022-03-03 ：第一次阅读

2022-06-05：第二次越读

 

论文解读目录