1 GAN基本概念

1.1 什么是生成对抗网络?

　　生成对抗网络(GAN, Generative adversarial network) 在 2014 年被 Ian Goodfellow 提出。

　　GAN 由生成器和判别器组成，生成器负责生成样本，判别器负责判断生成器生成的样本是否为真。生成器要尽可能迷惑判别器，而判别器要尽可能区分生成器生成的样本和真实样本。

　　在 GAN 的原作《Generative Adversarial Networks》中，作者将生成器比喻为印假抄票的犯罪分子，判别器则类比为警察。犯罪分子努力让钞票看起来逼真。警察则不断提升对于假仯的辨识能力。二者互相博弈，随着时间的进行，都会越来越强。那么类比于图像生成任务，生成器不断生成尽可能逼真的假图像。判别器则判断图像是否是真实的图像还是生成的图像，二者不断博弈优化。最终生成器生成的图像使得判别器完全无法判别真假。

　　举例：

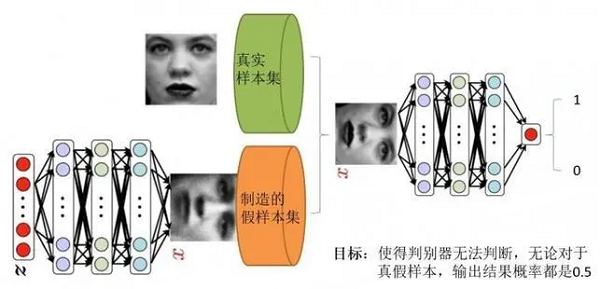
　　上述模型左边是生成器 $\mathrm{G}$ , 其输入是 $z$ , 对于原始的 $GAN$ ， $z$ 是由高斯分布随机采样得到的噪声。噪声 $z$ 通过生成器得到了生成的假样本。
　　生成的假样本与真实样本放到一起，被随机抽取送入到判别器 $D$ ，由判别器去区分输入的样本是生成的假样本还是真实的样本。整个过程简单明了, 生成对抗网络中的 “生成对抗” 主要体现在生成器和判别器之间的对抗。

1.2 GAN的目标函数是什么?　　

　　对于上述神经网络模型，如果想要学习其参数，首先需要一个目标函数。

　　GAN 的目标函数定义如下：

　　　　 $\underset{G}{min}\; \underset{D}{max}\; V(D, G)=\mathrm{E}_{x \sim p_{\text {data }}(x)}[\log D(x)]+\mathrm{E}_{z \sim p_{z}(z)}[\log (1-D(G(z)))]$

　　这个目标函数可以分为两个部分来理解:

　　判别器的优化通过 $\max _{D} V(D, G)$ 实现， $V(D, G)$ 为判别器的目标函数，

- 第一项 $\mathrm{E}_{x \sim p_{\text {data }}(x)}[\log D(x)]$ 表示对于从真实数据分布中采用的样本，其被判别器判定为真实样本概率的数学期望。对于真实数据分布中采样的样本，其预测为正样本的概率当然是越接近 $1$ 越好。因此希望最大化这一项。
- 第二项 $\mathrm{E}_{z \sim p_{z}(z)}[\log (1-D(G(z)))]$ 表示：对于从噪声 $P_{ \mathrm{z}}(\mathrm{z})$ 分布当中采样得到的样本经过生成器生成之后得到的生成图片, 然后送入判别器，判别器希望尽可能将生成样本都判别为生成样本（ $D(G(z))$ 值越接近 $0$ 。从而相当于最大化 $\log (1-D(G(z)))$ 的期望 $\mathrm{E}_{z \sim p_{z}(z)}[\log (1-D(G(z)))]$ 。

　　生成器的优化通过 $\underset{G}{min}\left( \underset{D}{max} V(D, G)\right)$ 实现。

- 注意，生成器的目标不是 $\underset{G}{min} \;V(D, G)$ ，即生成器不是最小化判别器的目标函数，生成器最小化的是判别器目标函数的最大值。判别器目标函数的最大值代表的是真实数据分布与生成数据分布的JS散度，JS散度可以度量分布的相似性，两个分布越接近，JS散度越小。

1.3 GAN的目标函数和交叉熵有什么区别?

　　回顾交叉熵：《损失函数｜交叉熵损失函数》

　　　　 $H(p, q)=-\sum\limits _{x} p(x) \log q(x)$

　　因为其中表示信息量的项来自于非真实分布 $q(x)$ ，而对其期望值的计算采用的是真实分布 $p(x)$ ，所以称其为交叉熵。

　　(1) 二分类交叉熵
　　在二分的情况下，模型最后需要预测的结果只有两种情况，对于每个类别我们的预测得到的概率为 $p$ 和 $1-p$ ，此时表达式为：
　　　　 $L=\frac{1}{N} \sum \limits _{i} L_{i}=\frac{1}{N} \sum \limits_{i}-\left[y_{i} \cdot \log \left( \ p_{i}\right)+\left(1-y_{i}\right) \cdot \log \left(1-p_{i}\right)\right]$
　　其中：

- $y_{i}$ 表示样本 $i$ 的 $label$ , 正类为 $1$ ，负类为 $0$ 。
- $p_{i}$ 表示样本 $i$ 预测为正类的概率。

　　(2) 多分类交叉熵

　　多分类的情况实际上就是对二分类的扩展：
　　　　 $L=\frac{1}{N} \sum \limits _{i} L_{i}=\frac{1}{N} \sum \limits _{i}-\sum \limits _{c=1}^{M} y_{i c} \log \left(p_{i c}\right)$
　　其中:

- $M$ 一一类别的数量
- $y_{i c}$ 一一符号函数 $(0\ 或 \ 1 ）$ ，如果样本 $i$ 的真实类别等于 $c$ 取 $1$ ，否则取 $0$ 。
- $p_{i c}$ 一一观测样本 $i$ 属于类别 $c$ 的预测概率

　　言归正传：

　　判别器目标函数写成离散形式即为:

　　　　 $V(D, G)=-\frac{1}{m} \sum\limits_{i=1}^{i=m} \log D\left(x^{i}\right)-\frac{1}{m} \sum\limits _{i=1}^{i=m} \log \left(1-D\left(\tilde{x}^{i}\right)\right)$

　　可以看出，这个目标函数和交叉熵是一致的，即判别器的目标是最小化交叉樀损失，生成器的目标是最小化生成数据分布和真实数据分布的JS散度。

1.4 GAN的LOSS 为什么降不下去?

　　对于很多 GAN 的初学者在实践过程中可能会纳闷，为什么GAN 的 Loss 一直降不下去。GAN到底什么时候才算收敛? 其实，作为一个训练良好的 GAN，其 Loss 就是降不下去的。衡量 GAN 是否训练好了, 只能由人肉眼去看生成的图片质量是否好。不过，对于没有一个很好的评价是否收敛指标的问，也有许多学者做了一些研究，后文提及的 WGAN 就提出了一种新的 Loss 设计方式，较好的解决了难以判断收敛性的问题。

　　下面我们分析一下 GAN 的 Loss为什么降不下去?

　　对于判别器而言，GAN 的 Loss 如下：

　　　　 $\underset{G}{min}\; \underset{D}{max}\; V(D, G)=\mathrm{E}_{x \sim p_{\text {data }}(x)}[\log D(x)]+\mathrm{E}_{z \sim p_{z}(z)}[\log (1-D(G(z)))]$

　　从 $\underset{G}{min}\; \underset{D}{max}\; V(D, G)$ 可以看出，生成器和判别器的目的相反，即生成器网络和判别器网络互为对抗，此消彼长。不可能Loss一直降到一个收敛的状态。

对于生成器，其 Loss 下降快，很有可能是判别器太弱，导致生成器很轻易的就"愚弄"了判别器。
对于判别器，其 Loss 下降快，意味着判别器很强，判别器很强则说明生成器生成的图像不够逼真，才使得判别器轻易判别，导致 Loss 下降很快。

　　也就是说，无论是判别器，还是生成器。Loss 的高低不能代表生成器的好坏。一个好的 GAN 网络，其 Loss 往往是不断波动的。看到这里可能有点让人绝望，似乎判断模型是否收敛就只能看生成的图像质量了。实际上，后文探讨的 WGAN，提出了一种新的 Loss 度量方式，让我们可以通过一定的手段来判断模型是否收敛。

2 生成式模型、判别式模型的区别?

　　对于机器学习模型，我们可以根据模型对数据的建模方式将模型分为两大类，生成式模型和判别式模型。

如果我们要训练一个关于猫狗分类的模型，对于判别式模型，只需要学习二者差异即可，比如说猫的体型会比狗小一点。
而生成式模型则不一样，需要学习猫是什么样，狗是什么样。有了二者的长相以后，再根据长相去区分。

　　具体而言：

生成式模型：由数据学习联合概率分布 $\mathrm{P}(\mathrm{X}, \mathrm{Y})$ ，然后由 $\mathrm{P}(\mathrm{Y} \mid \mathrm{X})=\mathrm{P}(\mathrm{X}, \mathrm{Y}) / \mathrm{P}(\mathrm{X})$ 求出概率分布 $\mathrm{P}(\mathrm{Y} \mid \mathrm{X})$ 作为预测的模型。该方法表示了给定输入 $X$ 与产生输出 $Y$ 的生成关系
判别式模型：由数据直接学习决策函数 $Y=f(X)$ 或条件概率分布 $P(Y \mid X)$ 作为预测模型，即判别模型。判别方法关心的是对于给定的输入 $X$ ，应该预测什么样的输出 $Y$ 。

　　对于上述两种模型，从文字上理解起来似乎不太直观。我们举个例子来阐述一下：

假如我有以下独立同分布的若干样本 $(x, y)$ ，其中 $x$ 为特征， $y$ 为标注， $y \in \{-1 ,1 \}$ ，这里有 $(x, y) \in\{(2,-1),(2,-1),(3,-1),(3,1),(3,1)\}$ 则:
- 生成模型：

　　　　　　 $\begin{array}{|c|r|l|}\hline p(x, y) & y=-1 & y=1 \\\hline x=2 & 2 / 5 & 0 \\\hline x=3 & 1 / 5 & 2 / 5 \\\hline\end{array}$

- 判别模型：

　　　　　　 $\begin{array}{|c|r|l|}\hline p(y \mid x) & y=-1 & y=1 \\\hline x=2 & 1 & 0 \\\hline x=3 & 1 / 3 & 2 / 3 \\\hline\end{array}$

3 什么是 mode collapsing?

　　即：某个模式(mode)出现大量重复样本, 例如:

　　上图左侧的蓝色五角星表示真实样本空间，黄色的是生成的。生成样本缺乏多样性，存在大量重复。比如上图右侧中，红框里面人物反复出现。

3.1 如何解决mode collapsing?

针对目标函数的改进方法

　　为了避免前面提到的由于优化 max min 导致 mode 跳来跳去的问题。

采用修改生成器 Loss 来解决。具体而言，UnrolledGAN 在更新生成器时更新 $k$ 次生成器，参考的 Loss 不是某一次的Loss，是判别器后面 $k$ 次迭代的 Loss。注意，判别器后面 $\mathrm{k}$ 次迭代不更新自己的参数，只计算 Loss 用于更新生成器。这种方式使得生成器考虑到了后面 $k$ 次判别器的变化情况，避免在不同 mode 之间切换导致的模式崩溃问题。此处务必和迭代 $k$ 次生成器，然后迭代 $1$ 次判别器区分开。
DRAGAN 则引入博亦论中的无后悔算法，改造其 Loss 以解决 mode collapse 问题。
EBGAN 则是加入 VAE 的重构误差以解决 mode collapse。

针对网络结构的改进方法
Multi agent diverse GAN(MAD-GAN)采用多个生成器，一个判别器以保障样本生成的多样性。具体结构如下:

　　　　相比于普通GAN，多了几个生成器，且在 Loss 设计的时候，加入一个正则项。正则项使用余弦距离惩罚三个生成器生成样本的一致性。

MRGAN 则添加了一个判别器来惩罚生成样本的 mode collapse 问题。具体结构如下:

　　输入样本 $x$ 通过一个 Encoder 编码为隐变量 $E(x)$ ，然后隐变量被 Generator 重构，训练时， Loss 有三个。 $D_{M}$ 和 $R$ (重构误差) 用于指导生成 real-like 的样本。而 $D_{D}$ 则对 $E(x)$ 和 $z$ 生成的样本进行判别，显然二者生成样本都是 fake samples，所以这个判别器主要用于判断生成的样本是否具有多样性，即是否出现 mode collapse。

Mini-batch Discrimination

　　Mini-batch discrimination 在判别器的中间层建立一个 mini-batch layer 用于计算基于 L1 距离的样本统计量，通过建立该统计量，实现了一个 batch 内某个样本与其他样本有多接近。这个信息可以被判别器利用到，从而甄别出哪些缺乏多样性的样本。对生成器而言，则要试图生成具有多样性的样本。

4 如何客观评价GAN的生成能力?

　　最常见评价 GAN 的方法就是主观评价。主观评价需要花费大量人力物力，且存在以下问题：

- 评价带有主管色彩，有些 bad case 没看到很容易造成误判
- 如果一个GAN过拟合了，那么生成的样本会非常真实，人类主观评价得分会非常高，可是这并不是一个好的GAN。

　　因此，就有许多学者提出了 GAN 的客观评价方法。

4.1 Inception Score

　　对于一个在 ImageNet 训练良好的 GAN，其生成的样本丢给 Inception 网络进行测试的时候，得到的判别概率应该具有如下特性:

对于同一个类别的图片, 其输出的概率分布应该趋向于一个脉冲分布。可以保证生成样本的准确性。
对于所有类别，其输出的概率分布应该趋向于一个均匀分布，这样才不会出现 mode dropping 等，可以保证生成样本的多样性。

　　因此，可以设计如下指标: $I S\left(P_{g}\right)=e^{E_{x \sim P_{g}}\left[K L\left(p_{M}(y \mid x) \| p_{M}(y)\right)\right]}$ 根据前面分析，如果是一个训练良好的 GAN， $p_{M}(y \mid x)$ 趋近于脉冲分布， $p_{M}(y)$ 趋近于均匀分布。二者 KL 散度会很大。Inception Score 自然就高。实际实验表明，Inception Score 和人的主观判别趋向一致。IS 的计算没有用到真实数据，具体值取决于模型 M 的选择。

　　特点: 可以一定程度上衡量生成样本的多样性和准确性，但是无法检测过拟合。 Mode Score也是如此。不推荐在和 ImageNet 数据集差别比较大的数据上使用。

4.2 Mode Score

　　Mode Score 作为 Inception Score 的改进版本，添加了关于生成样本和真实样本预测的概率分布相似性度量一项。

　　具体公式如下:

　　　　 $M S\left(P_{g}\right)=e^{E_{x \sim P_{g}}\left[K L\left(p_{M}(y \mid x) \| p_{M}(y)\right)-K L\left(p_{M}(y) \| p_{M}\left(y^{*}\right)\right)\right]}$

4.3 Kernel MMD (Maximum Mean Discrepancy)

　　计算公式如下:

　　　　 $M M D^{2}\left(P_{r}, P_{g}\right)=E_{x_{r} \sim P_{r}, x_{g} \sim P_{g}}\left[\left\|\sum_{i=1}^{n 1} k\left(x_{r}\right)-\sum_{i=1}^{n 2} k\left(x_{g}\right)\right\|\right]$

　　对于 Kernel MMD 值的计算，首先需要选择一个核函数 $k$ ，这个核函数把样本映射到再生希尔伯特空间(Reproducing Kernel Hilbert Space, RKHS), RKHS相比欧几里得空间有许多优点，对于函数内积的计算是完备的。将上述公式展开即可得到下面的计算公式:

　　　　 $M M D^{2}\left(P_{r}, P_{g}\right)=E_{x_{r}, x_{r}^{\prime} \sim P_{r}, x_{g}, x_{g^{\prime}} \sim P_{g}}\left[k\left(x_{r}, x_{r}{ }^{\prime}\right)-2 k\left(x_{r}, x_{g}\right)+k\left(x_{g}, x_{g}{ }^{\prime}\right)\right]$

　　MMD值越小，两个分布越接近。

　　特点: 可以一定程度上衡量模型生成图像的优劣性，计算代价小。

4.4 Wasserstein distance

　　Wasserstein distance 在最优传输问题中通常也叫做推土机距离。这个距离的介绍在 WGAN 中有详细讨论。

　　公式如下:

　　　　 $\begin{array}{c} &W D\left(P_{r}, P_{g}\right)=\underset{\omega \in \mathbb{R}^{m \times n}}{min} \sum\limits _{i=1}^{n} \sum\limits_{i=1}^{m} \omega_{i j} d\left(x_{i}^{r}, x_{j}^{g}\right) \\s.t. &\Sigma_{i=1}^{m} w_{i, j}=p_{r}\left(x_{i}^{r}\right), \forall i ;\\&\Sigma_{j=1}^{n} w_{i, j}=p_{g}\left(x_{j}^{g}\right), \forall j\end{array}$

　　Wasserstein distance 可以衡量两个分布之间的相似性。距离越小, 分布越相似。
　　特点: 如果特征空间选择合适，会有一定的效果。但是计算复杂度为 $O\left(n^{3}\right)$ 太高。

4.5 Fréchet Inception Distance (FID)

　　FID 距离计算真实样本，生成样本在特征空间之间的距离。首先利用 Inception 网络来提取特征，然后使用高斯模型对特征空间进行建模。根据高斯模型的均值和协方差来进行距离计算。

　　具体公式如下:

　　　　 $F I D\left(\mathbb{P}_{r}, \mathbb{P}_{g}\right)=\left\|\mu_{r}-\mu_{g}\right\|+\operatorname{Tr}\left(C_{r}+C_{g}-2\left(C_{r} C_{g}\right)^{1 / 2}\right)$

　　 $\mu$ ， $C$ 分别代表协方差和均值。

　　特点：尽管只计算了特征空间的前两阶矩，但是鲁棒，且计算高效。

4.6 1-Nearest Neighbor classifier

　　使用留一法，结合1-NN分类器 (别的也行) 计算真实图片，生成图像的精度。如果二者接近，则精度接近 50 % ，否则接近 0% 。对于 GAN的评价问题，作者分别用正样本的分类精度，生成样本的分类精度去衡量生成样本的真实性，多样性。

对于真实样本 $x_{r}$ ，进行 1-NN 分类的时候，如果生成的样本越真实。则真实样本空间 $\mathbb{R}$ 将被生成的样本 $x_{g}$ 包围。那么 $x_{r}$ 的精度会很低。
对于生成的样本 $x_{g}$ ，进行 1-NN 分类的时候，如果生成的样本多样性不足。由于生成的样本聚在几个mode，则 $x_{g}$ 很容易就和 $x_{r}$ 区分，导致精度会很高。