论文解读(DFCN)《Deep Fusion Clustering Network》
论文信息
论文标题:Deep Fusion Clustering Network
论文作者:Wenxuan Tu, Sihang Zhou, Xinwang Liu, Xifeng Guo, Zhiping Cai, En Zhu, Jieren Cheng
论文来源:2020, AAAI
论文地址:download
论文代码:download
1 Introduction
先前工作存在的问题:
-
- 缺少一种动态融合机制将属性信息和结构信息融合起来;
- 无法从目标分布提取有用的信息;
深度图聚类的方法可以分为以下几种:
-
- 首先,我们从局部和全局层面整合两种样本嵌入来进行共识表示学习。
- 之后,通过估计潜在嵌入空间中样本点和预先计算的聚类中心之间的相似性,我们得到了更精确的目标分布。
- 最后,我们设计了一种三元组自我监督机制,利用目标分布同时为AE、GAE和信息融合部分提供更可靠的指导。
我们开发了一种改进的具有对称结构的图自动编码器(IGAE),并利用图解码器重构的潜在表示和特征表示重构了邻接矩阵。
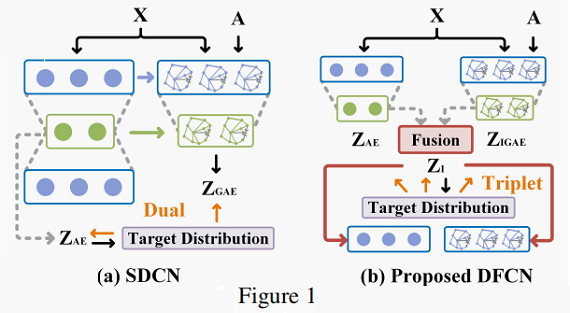
2 Method
模型可以分为四个部分:
-
- an autoencoder.
- an improved graph autoencoder.
- a fusion module.
- the optimization targets

class IGAE_encoder(nn.Module):
def __init__(self, gae_n_enc_1, gae_n_enc_2, gae_n_enc_3, n_input):
super(IGAE_encoder, self).__init__()
self.gnn_1 = GNNLayer(n_input, gae_n_enc_1)
self.gnn_2 = GNNLayer(gae_n_enc_1, gae_n_enc_2)
self.gnn_3 = GNNLayer(gae_n_enc_2, gae_n_enc_3)
self.s = nn.Sigmoid()
def forward(self, x, adj):
z = self.gnn_1(x, adj, active=False if opt.args.name == "hhar" else True)
z = self.gnn_2(z, adj, active=False if opt.args.name == "hhar" else True)
z_igae = self.gnn_3(z, adj, active=False)
z_igae_adj = self.s(torch.mm(z_igae, z_igae.t()))
return z_igae, z_igae_adj
class IGAE_decoder(nn.Module):
def __init__(self, gae_n_dec_1, gae_n_dec_2, gae_n_dec_3, n_input):
super(IGAE_decoder, self).__init__()
self.gnn_4 = GNNLayer(gae_n_dec_1, gae_n_dec_2)
self.gnn_5 = GNNLayer(gae_n_dec_2, gae_n_dec_3)
self.gnn_6 = GNNLayer(gae_n_dec_3, n_input)
self.s = nn.Sigmoid()
def forward(self, z_igae, adj):
z = self.gnn_4(z_igae, adj, active=False if opt.args.name == "hhar" else True)
z = self.gnn_5(z, adj, active=False if opt.args.name == "hhar" else True)
z_hat = self.gnn_6(z, adj, active=False if opt.args.name == "hhar" else True)
z_hat_adj = self.s(torch.mm(z_hat, z_hat.t()))
return z_hat, z_hat_adj
class IGAE(nn.Module):
def __init__(self, gae_n_enc_1, gae_n_enc_2, gae_n_enc_3, gae_n_dec_1, gae_n_dec_2, gae_n_dec_3, n_input):
super(IGAE, self).__init__()
self.encoder = IGAE_encoder(
gae_n_enc_1=gae_n_enc_1,
gae_n_enc_2=gae_n_enc_2,
gae_n_enc_3=gae_n_enc_3,
n_input=n_input)
self.decoder = IGAE_decoder(
gae_n_dec_1=gae_n_dec_1,
gae_n_dec_2=gae_n_dec_2,
gae_n_dec_3=gae_n_dec_3,
n_input=n_input)
def forward(self, x, adj):
z_igae, z_igae_adj = self.encoder(x, adj)
z_hat, z_hat_adj = self.decoder(z_igae, adj)
adj_hat = z_igae_adj + z_hat_adj
return z_igae, z_hat, adj_hat

class AE_encoder(nn.Module):
def __init__(self, ae_n_enc_1, ae_n_enc_2, ae_n_enc_3, n_input, n_z):
super(AE_encoder, self).__init__()
self.enc_1 = Linear(n_input, ae_n_enc_1)
self.enc_2 = Linear(ae_n_enc_1, ae_n_enc_2)
self.enc_3 = Linear(ae_n_enc_2, ae_n_enc_3)
self.z_layer = Linear(ae_n_enc_3, n_z)
self.act = nn.LeakyReLU(0.2, inplace=True)
def forward(self, x):
z = self.act(self.enc_1(x))
z = self.act(self.enc_2(z))
z = self.act(self.enc_3(z))
z_ae = self.z_layer(z)
return z_ae
class AE_decoder(nn.Module):
def __init__(self, ae_n_dec_1, ae_n_dec_2, ae_n_dec_3, n_input, n_z):
super(AE_decoder, self).__init__()
self.dec_1 = Linear(n_z, ae_n_dec_1)
self.dec_2 = Linear(ae_n_dec_1, ae_n_dec_2)
self.dec_3 = Linear(ae_n_dec_2, ae_n_dec_3)
self.x_bar_layer = Linear(ae_n_dec_3, n_input)
self.act = nn.LeakyReLU(0.2, inplace=True)
def forward(self, z_ae):
z = self.act(self.dec_1(z_ae))
z = self.act(self.dec_2(z))
z = self.act(self.dec_3(z))
x_hat = self.x_bar_layer(z)
return x_hat
class AE(nn.Module):
def __init__(self, ae_n_enc_1, ae_n_enc_2, ae_n_enc_3, ae_n_dec_1, ae_n_dec_2, ae_n_dec_3, n_input, n_z):
super(AE, self).__init__()
self.encoder = AE_encoder(
ae_n_enc_1=ae_n_enc_1,
ae_n_enc_2=ae_n_enc_2,
ae_n_enc_3=ae_n_enc_3,
n_input=n_input,
n_z=n_z)
self.decoder = AE_decoder(
ae_n_dec_1=ae_n_dec_1,
ae_n_dec_2=ae_n_dec_2,
ae_n_dec_3=ae_n_dec_3,
n_input=n_input,
n_z=n_z)
def forward(self, x):
z_ae = self.encoder(x)
x_hat = self.decoder(z_ae)
return x_hat, z_ae
2.1 Notations
$\widetilde{\mathbf{A}} \in \mathbb{R}^{N \times N}= \mathbf{D}^{-\frac{1}{2}}(\mathbf{A}+\mathbf{I}) \mathbf{D}^{-\frac{1}{2}} $。
Table 1 总结了所有符号。

2.2 Fusion-based Autoencoders
2.2.1 Input of the Decoder
首先整合GAE和AE学到的特征以获得共通的潜在表示。然后将这种嵌入作为输入,AE和GAE的解码器对两个子网络的输入进行重构。
2.2.2 Improved Graph Autoencoder
使用 IGAE 同时重构属性信息和结构信息,IGAE 编码器和解码器如下:
$\mathbf{Z}^{(l)}=\sigma\left(\widetilde{\mathbf{A}} \mathbf{Z}^{(l-1)} \mathbf{W}^{(l)}\right)\quad \quad \quad (1)$
$\widehat{\mathbf{Z}}^{(h)}=\sigma\left(\widetilde{\mathbf{A}} \widehat{\mathbf{Z}}^{(h-1)} \widehat{\mathbf{W}}^{(h)}\right)\quad \quad \quad (2)$
其中
-
- $\mathbf{W}^{(l)}$ 和 $\widehat{\mathbf{W}}^{(h)}$ 代表编码器层和解码器层参数矩阵;
IGAE 的损失函数如下:
$L_{I G A E}=L_{w}+\gamma L_{a}\quad \quad \quad (3)$
其中:
$L_{w} =\frac{1}{2 N}\|\widetilde{\mathbf{A}} \mathbf{X}-\widehat{\mathbf{Z}}\|_{F}^{2}\quad \quad \quad (4)$
$L_{a} =\frac{1}{2 N}\|\widetilde{\mathbf{A}}-\widehat{\mathbf{A}}\|_{F}^{2}\quad \quad \quad (5)$
2.2.3 Structure and Attribute Information Fusion
Structure and attribute information fusion (SAIF) module 包括两部分:
-
- a crossmodality dynamic fusion mechanism.
- a triplet selfsupervised strategy.
SAIF 模块如 Fig. 2 所示:

Part 1 :Cross-modality Dynamic Fusion Mechanism.
- 首先, 分别计算 $\mathrm{AE} \left(\mathbf{Z}_{A E} \in \mathbb{R}^{N \times d^{\prime}}\right)$ 和 IGAE $\left(\mathbf{Z}_{I G A E} \in \mathbb{R}^{N \times d^{\prime}}\right)$ 的潜在表示,然后进行线性组合:
$\mathbf{Z}_{I}=\alpha \mathbf{Z}_{A E}+(1-\alpha) \mathbf{Z}_{I G A E}\quad \quad \quad (6)$
- 其次,用类似图卷积的操作处理组合信息 $\mathbf{Z}_{I}$。通过这个操作,我们通过考虑数据中的局部结构来增强初始融合嵌入 $\mathbf{Z}_{I} \in \mathbb{R}^{N \times d^{\prime}}$ :
$ \mathbf{Z}_{L}=\widetilde{\mathbf{A}} \mathbf{Z}_{I}\quad \quad \quad (7)$
$\mathbf{Z}_{L} \in \mathbb{R}^{N \times d^{\prime}}$ 表示对 $\mathbf{Z}_{I}$ 局部结构增强。
- 第三, 进一步引入自相关学习机制来利用样本间初步信息融合空间中的非局部关系。我们首先通过 $Eq.8$ 计算归一化自相关矩阵 $\mathbf{S} \in \mathbb{R}^{N \times N}$:
${\large \mathbf{S}_{i j}=\frac{e^{\left(\mathbf{Z}_{L} \mathbf{Z}_{L}^{\mathrm{T}}\right)_{i j}}}{\sum\limits _{k=1}^{N} e^{\left(\mathbf{Z}_{L} \mathbf{Z}_{L}^{\mathrm{T}}\right)_{i k}}}} \quad \quad \quad (8)$
然后,计算全局相关性:
$\mathbf{Z}_{G}=\mathbf{S} \mathbf{Z}_{L}$ .
- 最后,我们采用跳跃连接来鼓励信息在融合机制内顺利传递:
$\widetilde{\mathbf{Z}}=\beta \mathbf{Z}_{G}+\mathbf{Z}_{L} \quad \quad \quad (9)$
Part 2 :Triplet Self-supervised Strategy
从 AE 和 IGAE 生成聚类嵌入 $\widetilde{\mathbf{Z}} \in \mathbb{R}^{N \times d^{\prime}}$ 来指导聚类学习。
- 生成目标分布:
${\large q_{i j}=\frac{\left(1+\left\|\tilde{z}_{i}-u_{j}\right\|^{2} / v\right)^{-\frac{v+1}{2}}}{\sum_{j^{\prime}}\left(1+\left\|\tilde{z}_{i}-u_{j^{\prime}}\right\|^{2} / v\right)^{-\frac{v+1}{2}}}}\quad \quad \quad (10)$
- 生成辅助分布:
${\large p_{i j}=\frac{q_{i j}^{2} / \sum\limits _{i} q_{i j}}{\sum\limits _{j^{\prime}}\left(q_{i j^{\prime}}^{2} / \sum\limits _{i} q_{i j^{\prime}}\right)}} \quad \quad \quad (11)$
为了让网络作为一个整体训练,设计了一个三联聚类损失,通过下列的 KL散度计算:
$L_{K L}=\sum\limits _{i} \sum\limits_{j} p_{i j} \log \frac{p_{i j}}{\left(q_{i j}+q_{i j}^{\prime}+q_{i j}^{\prime \prime}\right) / 3}\quad \quad \quad (12)$
2.2.4 Joint loss and Optimization
整体学习目标由两个主要部分组成,即AE和IGAE的重建损失,以及与目标分布相关的聚类损失:
$L=\underbrace{L_{\text {AE }}+L_{\text {IGAE }}}_{\text {Reconstruction }}+\underbrace{\lambda L_{K L}}_{\text {Clustering }} .\quad \quad \quad (13)$
其中
-
- $L_{AE}$ 代表着 AE 的MSE 损失。
DFCN 算法如 Algorithm 1 所示:


class DFCN(nn.Module):
def __init__(self, ae_n_enc_1, ae_n_enc_2, ae_n_enc_3,
ae_n_dec_1, ae_n_dec_2, ae_n_dec_3,
gae_n_enc_1, gae_n_enc_2, gae_n_enc_3,
gae_n_dec_1, gae_n_dec_2, gae_n_dec_3,
n_input, n_z, n_clusters, v=1.0, n_node=None, device=None):
super(DFCN, self).__init__()
self.ae = AE(
ae_n_enc_1=ae_n_enc_1,
ae_n_enc_2=ae_n_enc_2,
ae_n_enc_3=ae_n_enc_3,
ae_n_dec_1=ae_n_dec_1,
ae_n_dec_2=ae_n_dec_2,
ae_n_dec_3=ae_n_dec_3,
n_input=n_input,
n_z=n_z)
self.gae = IGAE(
gae_n_enc_1=gae_n_enc_1,
gae_n_enc_2=gae_n_enc_2,
gae_n_enc_3=gae_n_enc_3,
gae_n_dec_1=gae_n_dec_1,
gae_n_dec_2=gae_n_dec_2,
gae_n_dec_3=gae_n_dec_3,
n_input=n_input)
self.a = nn.Parameter(nn.init.constant_(torch.zeros(n_node, n_z), 0.5), requires_grad=True).to(device)
self.b = 1 - self.a
self.cluster_layer = nn.Parameter(torch.Tensor(n_clusters, n_z), requires_grad=True)
torch.nn.init.xavier_normal_(self.cluster_layer.data)
self.v = v
self.gamma = Parameter(torch.zeros(1))
def forward(self, x, adj):
z_ae = self.ae.encoder(x)
z_igae, z_igae_adj = self.gae.encoder(x, adj)
z_i = self.a * z_ae + self.b * z_igae #Eq.6
z_l = torch.spmm(adj, z_i) #Eq.7
s = torch.mm(z_l, z_l.t())
s = F.softmax(s, dim=1) #Eq.8
z_g = torch.mm(s, z_l)
z_tilde = self.gamma * z_g + z_l #Eq.9
x_hat = self.ae.decoder(z_tilde)
z_hat, z_hat_adj = self.gae.decoder(z_tilde, adj)
adj_hat = z_igae_adj + z_hat_adj
q = 1.0 / (1.0 + torch.sum(torch.pow((z_tilde).unsqueeze(1) - self.cluster_layer, 2), 2) / self.v)
q = q.pow((self.v + 1.0) / 2.0)
q = (q.t() / torch.sum(q, 1)).t() #Eq.10
q1 = 1.0 / (1.0 + torch.sum(torch.pow(z_ae.unsqueeze(1) - self.cluster_layer, 2), 2) / self.v)
q1 = q1.pow((self.v + 1.0) / 2.0)
q1 = (q1.t() / torch.sum(q1, 1)).t() #Eq.10
q2 = 1.0 / (1.0 + torch.sum(torch.pow(z_igae.unsqueeze(1) - self.cluster_layer, 2), 2) / self.v)
q2 = q2.pow((self.v + 1.0) / 2.0)
q2 = (q2.t() / torch.sum(q2, 1)).t() #Eq.10
return x_hat, z_hat, adj_hat, z_ae, z_igae, q, q1, q2, z_tilde

def Train(epoch, model, data, adj, label, lr, pre_model_save_path, final_model_save_path, n_clusters,
original_acc, gamma_value, lambda_value, device):
optimizer = Adam(model.parameters(), lr=lr)
model.load_state_dict(torch.load(pre_model_save_path, map_location='cpu'))
with torch.no_grad():
x_hat, z_hat, adj_hat, z_ae, z_igae, _, _, _, z_tilde = model(data, adj)
kmeans = KMeans(n_clusters=n_clusters, n_init=20)
cluster_id = kmeans.fit_predict(z_tilde.data.cpu().numpy())
model.cluster_layer.data = torch.tensor(kmeans.cluster_centers_).to(device)
eva(label, cluster_id, 'Initialization')
for epoch in range(epoch):
# if opt.args.name in use_adjust_lr:
# adjust_learning_rate(optimizer, epoch)
x_hat, z_hat, adj_hat, z_ae, z_igae, q, q1, q2, z_tilde = model(data, adj)
tmp_q = q.data
p = target_distribution(tmp_q)
loss_ae = F.mse_loss(x_hat, data) #L_AE loss
loss_w = F.mse_loss(z_hat, torch.spmm(adj, data)) #Eq.4
loss_a = F.mse_loss(adj_hat, adj.to_dense()) #Eq.5
loss_igae = loss_w + gamma_value * loss_a #Eq.3
loss_kl = F.kl_div((q.log() + q1.log() + q2.log()) / 3, p, reduction='batchmean') #Eq.12
loss = loss_ae + loss_igae + lambda_value * loss_kl #Eq.13
print('{} loss: {}'.format(epoch, loss))
optimizer.zero_grad()
loss.backward()
optimizer.step()
kmeans = KMeans(n_clusters=n_clusters, n_init=20).fit(z_tilde.data.cpu().numpy())
acc, nmi, ari, f1 = eva(label, kmeans.labels_, epoch)
acc_reuslt.append(acc)
nmi_result.append(nmi)
ari_result.append(ari)
f1_result.append(f1)
if acc > original_acc:
original_acc = acc
torch.save(model.state_dict(), final_model_save_path)
3 Experiments
数据集

节点聚类
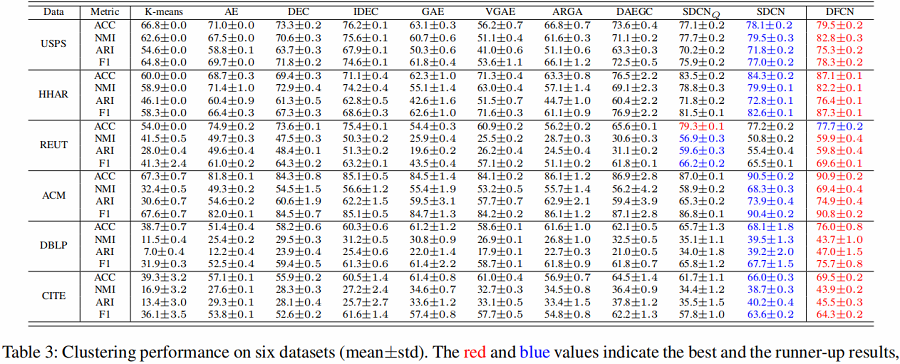
消融实验
IGAE 有效性分析

$GAE-L_{w}$ 或 $GAE-L_{a}$ 表示仅通过加权属性矩阵或邻接矩阵的重建损失函数进行优化的方法。
分析:
-
- $GAE-L _{w}$ 在六个数据集上的表现始终优于 $GAE-L _{a}$。
- 与仅构建邻接矩阵的方法相比,IGAE 明显提高了聚类性能。
SAIF 模块分析
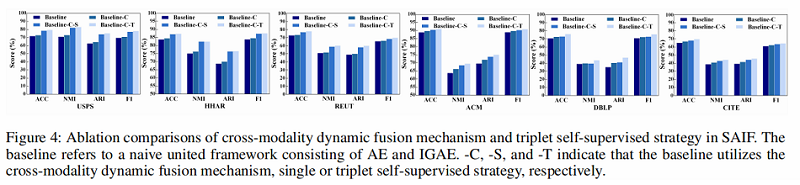
如 Fig. 4 所示,我们观察到
-
- 与baseline相比,Baseline-C方法有大约0.5%到5.0%的性能提升,表明从局部和全局层面探索图结构和节点属性有助于学习共识潜在表示以更好地聚类;
- Baseline-C-T 方法在所有数据集上的性能始终优于 Baseline-C-S 方法。 原因是我们的三元组自监督策略成功地为 AE、IGAE 和融合部分的训练生成了更可靠的指导,使它们相互受益。
- 与baseline相比,Baseline-C方法有大约0.5%到5.0%的性能提升,表明从局部和全局层面探索图结构和节点属性有助于学习共识潜在表示以更好地聚类;
双源信息的影响
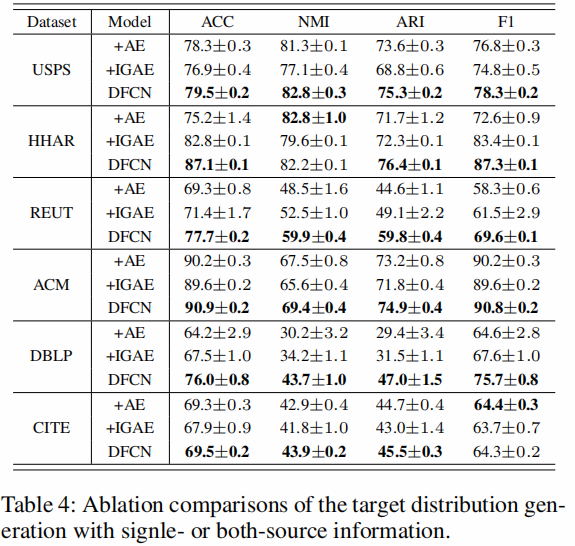
超参数 λ 分析
从 Eq. 13 中可以看出。 如图所示,DFCN 引入了超参数 $\lambda$ 以在重建和聚类之间进行权衡。
图 5 说明了当 $\lambda$ 从 $0.01$ 到 $100$ 变化时 DFCN 的性能变化。
、 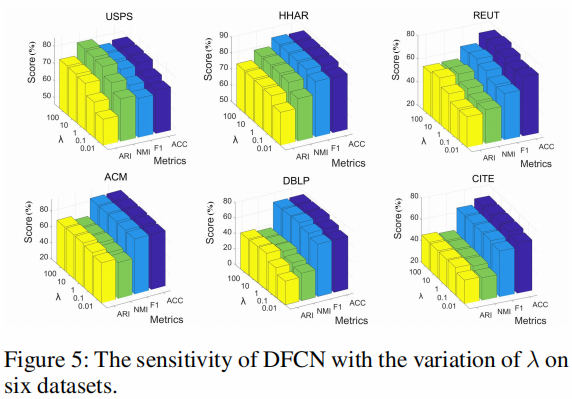
From these figures, we observe that
- the hyper-parameter $\lambda$ is effective in improving the clustering performance;
- the performance of the method is stable in a wide range of $\lambda$ ;
- $ \mathrm{DFCN}$ tends to perform well by setting $\lambda$ to $10$ across all datasets.
可视化
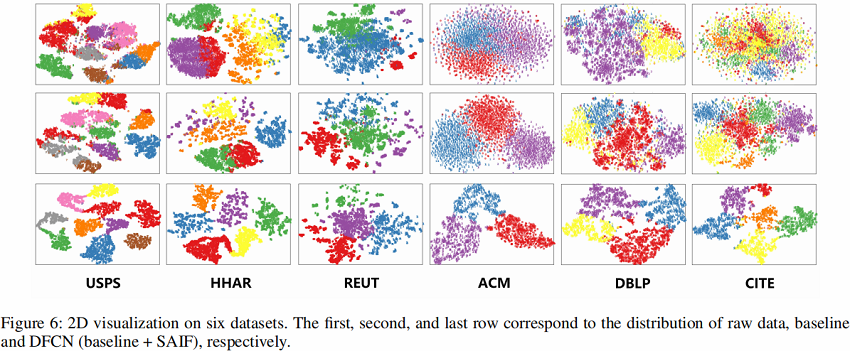
4 Conclusion
提出三联损失、引入双源信息输入。
修改历史
2022-01-27 创建文章
2022-06-07 精度论文,并附上代码
因上求缘,果上努力~~~~ 作者:图神经网络,转载请注明原文链接:https://www.cnblogs.com/BlairGrowing/p/15843269.html



