欧几里得数据与非欧几里得数据

前言

　　数据分为两类：欧几里得数据与非欧几里得数据

　　

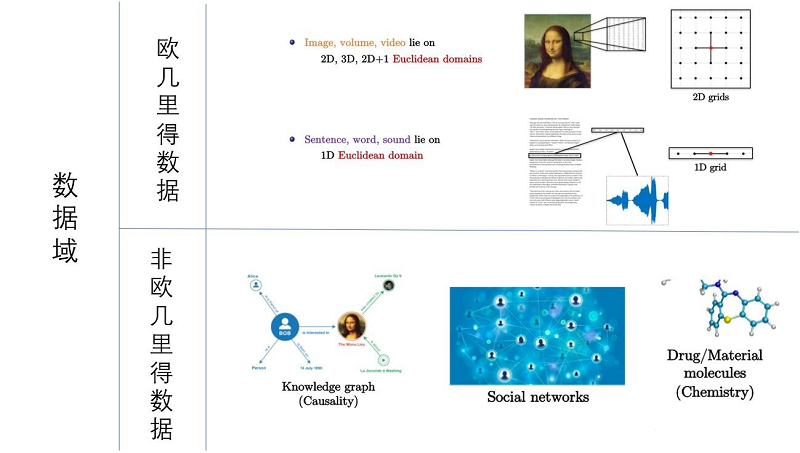
欧几里得数据

　　特点：“排列整齐”，是一类具有很好的平移不变性的数据。

　　图像中的平移不变性：即不管图像中的目标被移动到图片的哪个位置，得到的结果（标签）应该相同的。

　　对于这类数据以其中一个像素为中心点，其邻居节点的数量相同。可以很好的定义一个全局共享的卷积核来提取图像中相同的结构。常见这类数据有图像、文本、语言。

　　图像：图像是一种  $2D$  的网格类型数据，通常用矩阵进行存储。

　　文本：文本是一种  $1D$  的网格类型数据，通常可以用向量进行存储。对于文本，我们通常做法是去停用词、以及高频词（DIFT），最后嵌入到一个一维的向量空间。

 　　　　

 

 　　而且，因为这类型的数据排列整齐，不同样本之间可以容易的定义出  "距离"  这个概念出来。我们假设现在有两个图片样本，尽管其图片大小可能不一致，但是总是可以通过空间下采样的方式将其统一到同一个尺寸的，然后直接逐个像素点进行相减后取得平方和，求得两个样本之间的欧几里德距离是完全可以进行的。如下式所见：

　　　　$d(\mathbf{s_i}, \mathbf{s_j}) = \dfrac{1}{2}||\mathbf{s_i}-\mathbf{s_j}||^2$

　　因此，不妨把图片样本的不同像素点看成是高维欧几里德空间中的某个维度，因此一张  $m \times n$  的图片可以看成是  $m \times n$  维的欧几里德样本空间中的一个点，而不同样本之间的距离就体现在了样本点之间的距离了。

非欧几里得数据

　　它是一类不具有平移不变性的数据。这类数据以其中的一个为节点，其邻居节点的数量可能不同。常见这类数据有知识图谱、社交网络、化学分子结构等等。

　　非欧几里德结构的样本总得来说有两大类型，分别是图(Graph)数据和流形数据( manifolds)，如下图所示:

　　　　

 

 

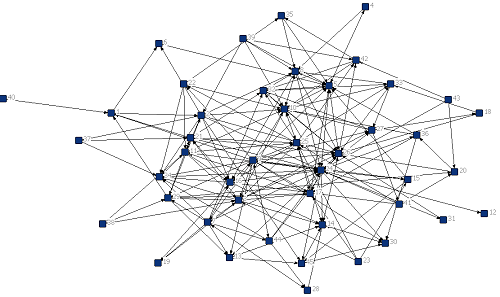
　　　　　　　　　　　　　　　　　　　　图数据

 

　　　　

 

 　　　　　　　　　　流形数据( manifolds)

　　这两类数据有个特点就是，排列不整齐，比较的随意。

　　具体体现在：对于数据中的某个点，难以定义出其邻居节点出来，或者是不同节点的邻居节点的数量是不同的，这个其实是一个特别麻烦的问题，因为这样就意味着难以在这类型的数据上定义出和图像等数据上相同的卷积操作出来，而且因为每个样本的节点排列可能都不同，比如在生物医学中的分子筛选中，显然这个是一个Graph数据的应用，但是我们都明白，不同的分子结构的原子连接数量，方式可能都是不同的，因此难以定义出其欧几里德距离出来，这个是和我们的欧几里德结构数据明显不同的。因此这类型的数据不能看成是在欧几里德样本空间中的一个样本点了，而是要想办法将其嵌入(embed)到合适的欧几里德空间后再进行度量。而我们现在流行的  Graph Neural Network  便可以进行这类型的操作。这就是我们的后话了。

---

　　另外，欧几里德结构数据所谓的“排列整齐”也可以视为是一种特殊的非欧几里德结构数据，比如说是一种特殊的Graph数据，如下图所示[5]：

 

　　　　

 

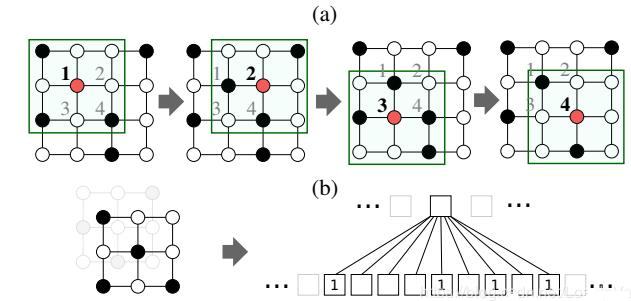
 　　因此，用Graph Neural Network的方法同样可以应用在欧几里德结构数据上，比如文献[6]中report的结果来看，的确这样是可行的。事实上，只要是赋范空间中的数据，都可以建立数据节点与数据节点之间的某种关联，都可以尝试用非欧几里德结构数据的深度方法进行实验