论文解读（DEC）《Unsupervised Deep Embedding for Clustering Analysis》

论文信息

论文标题：Unsupervised Deep Embedding for Clustering Analysis
论文作者：Junyuan Xie, Ross Girshick, Ali Farhadi
论文来源：2016,ICML
论文地址：download 
论文代码：download 

1 Introduction

　　本文提出一种同时学习特征表示和节点聚类的深度神经网路。　　

2 Method

　　DEC有两个阶段:

• • 用深度自编码器（deep autoencoder）参数初始化；
  • 参数优化，通过迭代计算辅助目标分布和最小化Kullback-Leibler(KL)散度；　

2.1 Clustering with KL divergence

　　给定非线性映射  $f_{\theta}$  和初始聚类质心 $ \left\{\mu_{j}\right\}_{j=1}^{k}$  的初始估计，我们建议改进聚类使用在两个步骤之间交替的无监督算法。

　　第一步，首先计算节点嵌入和质心之间的软分配 。

　　第二步，更新映射函数  $f_{\theta}$ ， 并通过使用辅助目标分布从当前的高置信度分配中学习来细化集群质心。 重复此过程，直到满足收敛标准。

2.1.1. Soft assignment 

　　使用 Student’s t-distribution 作为核来衡量节点嵌入 $z_i$  和质心  $\mu_{j}$  之间的相似性：

　　　　$q_{i j}=\frac{\left(1+\left\|z_{i}-\mu_{j}\right\|^{2} / \alpha\right)^{-\frac{\alpha+1}{2}}}{\sum_{j^{\prime}}\left(1+\left\|z_{i}-\mu_{j^{\prime}}\right\|^{2} / \alpha\right)^{-\frac{\alpha+1}{2}}} \quad \quad\quad\quad (1)$

　　其中：

• • $z_{i}=f_{\theta}\left(x_{i}\right) \in Z$  是嵌入后的  $x_{i} \in X$
  • $\alpha$  是  Student's  t  distribution 的自由度
  • $q_{i j}$  可以解释为将样本 $i$ 分配给聚类 $j$ 的概率（即软分配）

　　本文让  $α=1$  用于所有实验。

2.1.2 KL Divergence minimization

　　我们建议在 辅助分布 的帮助下，通过学习 高置信度分配 来迭代地细化聚类。

　　具体来说，本文通过匹配软分配到目标分布来训练的。为此，将目标定义为软分配  $q_i$  和辅助分布  $p_i$  之间的KL散度损失如下：

　　　　$L=\mathrm{KL}(P \| Q)=\sum \limits_{i} \sum \limits_{j} p_{i j} \log \frac{p_{i j}}{q_{i j}} \quad \quad\quad\quad (2)$

　　目标分布  $P$  的选择是  DEC  的性能的关键。一种简单的方法是将超过置信阈值的数据点的每个  $p_i$  设置为一个  $delta$  分布（到最近的质心），而忽略其余的。然而，由于  $q_i$  是软任务，所以使用较软的概率目标更自然和灵活。

　　　在实验中，我们计算  $p_i$，首先将  $q_i$  提高到二次幂，然后按每个簇的频率归一化：

　　　　${\large p_{i j}=\frac{q_{i j}^{2} / f_{j}}{\sum_{j^{\prime}} q_{i j^{\prime}}^{2} / f_{j^{\prime}}}} \quad \quad\quad\quad (3)$

　　其中  $f_{j}=\sum \limits _{i} q_{i j}$   是软聚类频率 。

2.1.3 Optimization

　　本文利用具有动量的随机梯度下降(SGD)联合优化了聚类中心  $\left\{\mu_{j}\right\} $  和 DNN参数  $\theta  $。

　　$L$ 对每个数据点  $z_i$  和每个聚类质心  $\mu_{j}$  的特征空间嵌入的梯度计算为：

　　　　$\frac{\partial L}{\partial z_{i}}=\frac{\alpha+1}{\alpha} \sum \limits _{j}\left(1+\frac{\left\|z_{i}-\mu_{j}\right\|^{2}}{\alpha}\right)^{-1}\quad \quad\quad\quad (4)$

　　　　$\frac{\partial L}{\partial \mu_{j}}=-\frac{\alpha+1}{\alpha} \sum \limits _{i}\left(1+\frac{\left\|z_{i}-\mu_{j}\right\|^{2}}{\alpha}\right)^{-1}\times\left(p_{i j}-q_{i j}\right)\left(z_{i}-\mu_{j}\right)\quad \quad\quad\quad (5)$

2.2 Parameter initialization

　　现在将讨论参数和质心是如何初始化的。

　　本文使用堆叠自动编码器(SAE) 初始化 DEC，SAE学习到的无监督表示能促进使用 DEC 进行聚类表示的学习。

　　SAE网络每一层都是一个去噪自动编码器。去噪自动编码器是定义为：

　　　　$\tilde{x} \sim \operatorname{Dropout}(x) \quad \quad\quad\quad (6)$

　　　　$h=g_{1}\left(W_{1} \tilde{x}+b_{1}\right) \quad \quad\quad\quad (7)$

　　　　$\tilde{h} \sim \operatorname{Dropout}(h) \quad \quad\quad\quad (8)$

　　　　$y=g_{2}\left(W_{2} \tilde{h}+b_{2}\right)\quad \quad\quad\quad (9)$

　　训练是通过最小化最小二乘损失  $\|x-y\|_{2}^{2}$  来完成的。

　　经过  greedy layer-wise training  后，我们将所有编码器层和所有解码器层，按反向层训练顺序连接起来，形成一个深度自动编码器，然后对其进行微调，使其最小化重构损失。最终的结果是一个中间有一个瓶颈编码层的多层深度自动编码器。然后我们丢弃解码器层，并使用编码器层作为数据空间和特征空间之间的初始映射，如 Fig. 1 所示。

　　　　

　　为了初始化聚类中心，我们将数据通过初始化的DNN传递，得到嵌入的数据点，然后在特征空间  $Z$  中执行标准的  $k-means$  聚类，得到  $k$  个初始质心  $\left\{\mu_{j}\right\}_{j=1}^{k}$。

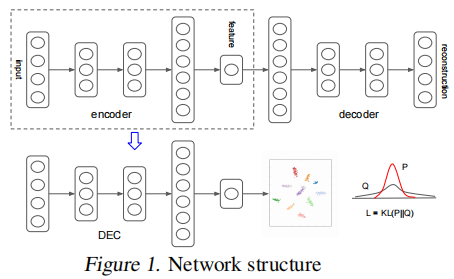
3 Experiments

数据集

　　

节点聚类

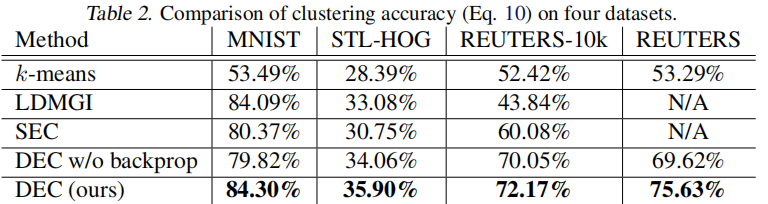
　　在 Table 2 中，报告了每种算法的最佳性能：

　　

4 Conclusion

　　本文提出了深度嵌入式聚类，即DEC，一种在联合优化的特征空间中聚集一组数据点的算法。DEC的工作原理是迭代优化基于KL散度的聚类目标和自训练目标分布。我们的方法可以看作是半监督自我训练的无监督扩展。我们的框架提供了一种方法来学习专门的表示，而没有基本聚类成员标签。

 

修改历史

2022-01-12 创建文章

2022-06-08 修订文章

 

论文解读目录