论文解读(SDCN)《Structural Deep Clustering Network》
论文信息
论文标题:Structural Deep Clustering Network
论文作者:Junyuan Xie, Ross Girshick, Ali Farhadi
论文来源:2020, WWW
论文地址:download
论文代码:download
1 Introduction
深度聚类同时考虑属性信息和结构信息。
-
- 属性信息采用 Autoencoder
- 结构信息采用 GCN
2 Method
在本节中,将介绍 SDCN,其整体框架如 Figure 1 所示。
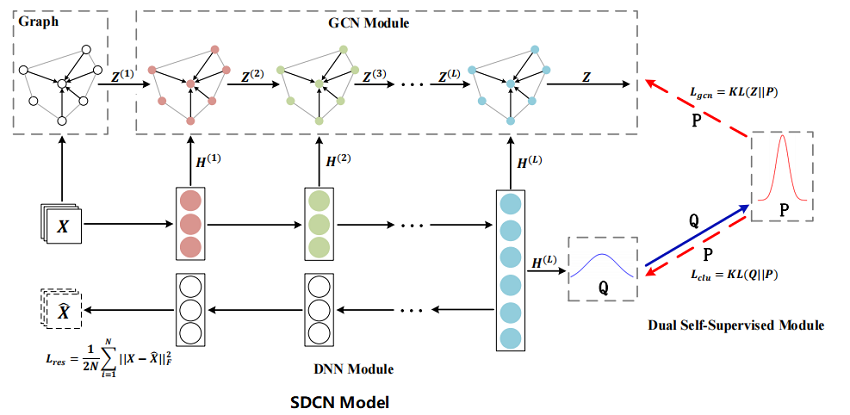
首先基于原始数据构建一个KNN图。
然后,将原始数据和 KNN 图分别输入到自动编码器和GCN中。并将每一层的自动编码器与相应的 GCN 层连接起来,这样就可以通过 delivery operator 将自动编码器特定的表示集成到 GCN 的表示中。
同时,我们提出了一种双重自监督机制来监督自动编码器和 GCN 的训练进程。本文将在下面详细描述我们提出的模型。
2.1 KNN Graph
假设我们有原始数据 $\mathrm{X} \in \mathbb{R}^{N \times d} $,其中每一行 $\mathbf{x}_{i}$ 代表 $i-th$ 样本,$N$ 是样本数,$d$ 是维度。 对于每个样本,我们首先找到它的 $top-K$ 相似邻居并设置边以将其与其邻居连接。 有很多方法可以计算样本的相似度矩阵 $S \in \mathbb{R}^{N} \times N$。
这里列出在构建 KNN 图时使用的两种相似度计算的流行方法:
- Heat Kernel. 样本 $i$ 和 $j$ 之间的相似度计算如下:
$ \mathrm{S}_{i j}=e^{-\frac{\left\|\mathrm{x}_{i}-\mathrm{x}_{j}\right\|^{2}}{t}}\quad \quad(1)$
其中, $t$ 为热传导方程中的时间参数。对于连续的数据,如:图像。
- Dot-product. 样本 $i$ 和样本 $j$ 之间的相似性的计算方法为:
$\mathrm{S}_{i j}=\mathbf{x}_{j}^{T} \mathbf{x}_{i} \quad \quad (2)$
对于离散数据,如: bag-of-words,使用点积相似性,使相似性只与相同 word 的数量相关。
在计算相似度矩阵 $S$ 后,选择每个样本的前 $k$ 个相似度点作为其邻居,构造一个无向的 $k$ 近邻图,从非图数据中得到邻接矩阵 $A$。
2.2 DNN Module
使用基本的自动编码器学习原始数据的表示。
Encoder 部分:
$\mathbf{H}^{(\ell)}=\phi\left(\mathbf{W}_{e}^{(\ell)} \mathbf{H}^{(\ell-1)}+\mathbf{b}_{e}^{(\ell)}\right) \quad \quad (3)$
Decoder 部分:
$\mathbf{H}^{(\ell)}=\phi\left(\mathbf{W}_{d}^{(\ell)} \mathbf{H}^{(\ell-1)}+\mathbf{b}_{d}^{(\ell)}\right) \quad \quad (4)$
DNN module 的目标函数:
$\mathcal{L}_{r e s}=\frac{1}{2 N} \sum \limits _{i=1}^{N}\left\|\mathbf{x}_{i}-\hat{\mathbf{x}}_{i}\right\|_{2}^{2}=\frac{1}{2 N}\|\mathbf{X}-\hat{\mathbf{X}}\|_{F}^{2}\quad \quad (5)$
2.3 GCN Module
自编码器能够从数据本身中学习有用的表示,例如 $\mathrm{H}^{(1)}$ , $\mathrm{H}^{(2)}$ , $\cdots$ , $\mathrm{H}^{(L)}$ ,但忽略了样本之间的关系。 在本节中,将介绍如何使用 GCN 模块来传播 DNN 模块生成的这些表示。 一旦将 DNN 模块学习到的所有表示都集成到 GCN 中,那么 GCN 可学习表示将能够适应两种不同类型的信息,即数据本身和数据之间的关系。
使用 $\mathrm{GCN}$ 来学习图结构信息:
$\mathrm{Z}^{(\ell)}=\phi\left(\widetilde{\mathrm{D}}^{-\frac{1}{2}} \widetilde{\mathrm{A}} \widetilde{\mathrm{D}}^{-\frac{1}{2}} \mathbf{Z}^{(\ell-1)} \mathbf{W}^{(\ell-1)}\right) \quad \quad (6)$
其中
-
- $\widetilde{\mathbf{A}}=\mathbf{A}+\mathbf{I}$
- $\widetilde{\mathbf{D}}_{ii}=\sum_{j} \widetilde{\mathbf {A}}_{\mathbf{ij}}$ , $\mathbf{I}$
接着讲自编码器学习到的表示 $\mathbf{H}^{(\ell-1)}$ 与 GCN 学到的表示 $\mathbf{Z}^{( \ell-1)}$ 结合起来:
$\widetilde{\mathbf{Z}}^{(\ell-1)}=(1-\epsilon) \mathbf{Z}^{(\ell-1)}+\epsilon \mathbf{H}^{(\ell-1)} \quad \quad (7)$
其中 $ϵ$ 是一个平衡系数,本文设为 $0.5$ 。
然后使用 $\widetilde{\mathbf{Z}}^{(\ell-1)}$ 作为 $\mathrm{GCN}$ 中 $l $ 层的输入来生成表示 $Z^{ (\ell)} $:
$\mathbf{Z}^{(\ell)}=\phi\left(\widetilde{\mathbf{D}}^{-\frac{1}{2}} \widetilde{\mathbf{A}} \widetilde{\mathbf{D}}^{-\frac{1}{2}} \widetilde{\mathbf{Z}}^{(\ell-1)} \mathbf{W}^{(\ell-1)}\right) \quad \quad (8)$
注意,第一层GCN的输入是原始数据 $X$:
$\mathrm{Z}^{(1)}=\phi\left(\widetilde{\mathbf{D}}^{-\frac{1}{2}} \widetilde{\mathrm{A}} \widetilde{\mathbf{D}}^{-\frac{1}{2}} \mathbf{X} \mathbf{W}^{(1)}\right) \quad \quad (9)$
GCN模块的最后一层是具有 softmax 功能的多分类层:
$Z=\operatorname{softmax}\left(\widetilde{\mathbf{D}}^{-\frac{1}{2}} \widetilde{\mathbf{A}} \widetilde{\mathbf{D}}^{-\frac{1}{2}} \mathbf{Z}^{(L)} \mathbf{W}^{(L)}\right) \quad \quad (10)$
结果 $z_{i j} \in Z$ 表示概率样本 $i$ 属于聚类中心 $j$ ,我们可以将 $Z$ 视为概率分布。
2.4 Dual Self-Supervised Module
在此,提出一个双自监督模块,它将自编码器和 GCN 模块统一在一个框架内,有效地对这两个模块进行端到端训练以进行聚类。
对于第 $i$ 个样本和第 $j$ 个簇,我们使用 Student’s t-distribution 来度量数据表示 $h_i$ 和簇中心向量 $µ_j$ 之间的相似性:
${\large q_{i j}=\frac{\left(1+\left\|\mathbf{h}_{i}-\boldsymbol{\mu}_{j}\right\|^{2} / v\right)^{-\frac{v+1}{2}}}{\sum_{j^{\prime}}\left(1+\left\|\mathbf{h}_{i}-\boldsymbol{\mu}_{j^{\prime}}\right\|^{2} / v\right)^{-\frac{v+1}{2}}}} \quad \quad (11)$
其中
-
- $\mathbf{h}_{i}$ 是 $\mathbf{H}^{(L)}$ 的第 $i$ 行;
- $\boldsymbol{\mu}_{j}$ 初始化为 $K -means$ 在预训练自动编码器学习的表征上;
- $v$ 是 Student’s t-distribution 的自由度,实验中设置为 $1$;
- $q_{i j}$ 可以认为是将样本 $i$ 分配给集群 $j$ 的概率,即软分配;
在获得聚类结果分布 $Q$ 后,本文目标是通过从高置信度分配中学习来优化数据表示。具体来说,希望使数据表示更接近集群中心,从而提高集群的凝聚力。因此,计算一个目标分布 $P$ 如下:
${\large p_{i j}=\frac{q_{i j}^{2} / f_{j}}{\sum_{j^{\prime}} q_{i j^{\prime}}^{2} / f_{j^{\prime}}}} \quad \quad (12)$
其中 $f_{j}=\sum_{i} q_{i j}$ 是软聚类频率。在目标分布 $P$ 中,对 $Q$ 中的每个分配进行平方和归一化,以便分配具有更高的置信度,采用 KL 散度来比较两类概率:
$\mathcal{L}_{c l u}=K L(P \| Q)=\sum \limits _{i} \sum\limits _{j} p_{i j} \log \frac{p_{i j}}{q_{i j}} \quad \quad (13)$
即:最小化 $Q$ 和 $P$ 分布之间的 $KL$ 散度损失。
目标分布 $P$ 可以帮助DNN模块学习更好的聚类任务表示,即使数据表示更接近聚类中心。这被认为是一个自监督机制,因为目标分布 $P$ 是由分布 $Q$ 计算出来的,而 $P$ 分布依次监督分布 $Q$ 的更新。
另一个自监督模块在:对于 GCN 模块的训练,GCN 模块也会出现提供一个聚类分配分布 $Z$ 。因此,可以使用分配 $P$ 来监督分配 $Z$ 如下:
$\mathcal{L}_{g c n}=K L(P \| Z)=\sum \limits_{i} \sum \limits _{j} p_{i j} \log \frac{p_{i j}}{z_{i j}}\quad \quad (14)$
通过这种机制,SDCN可将聚类目标和分类目标这两个不同的目标集中在一个损失函数中。 SDCN 的总损失函数是:
$\mathcal{L}=\mathcal{L}_{\text {res }}+\alpha \mathcal{L}_{\text {clu }}+\beta \mathcal{L}_{g c n}\quad \quad (15)$
当训练稳定后,可为样本设置标签。本文选择分布 $Z$ 中的软分配作为最终的聚类结果,因为 GCN 学习到的表示包含了两种不同类型的信息。分配给样本 $i$ 的标签是:
$r_{i}=\underset{j}{arg\ max} \ z_{i j}\quad \quad (16)$
算法流程:

3 Experiments
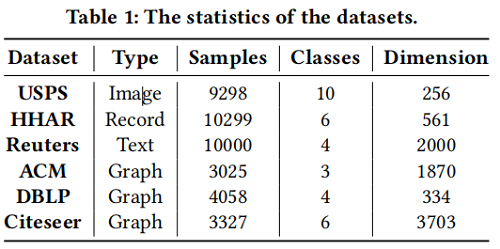
节点聚类
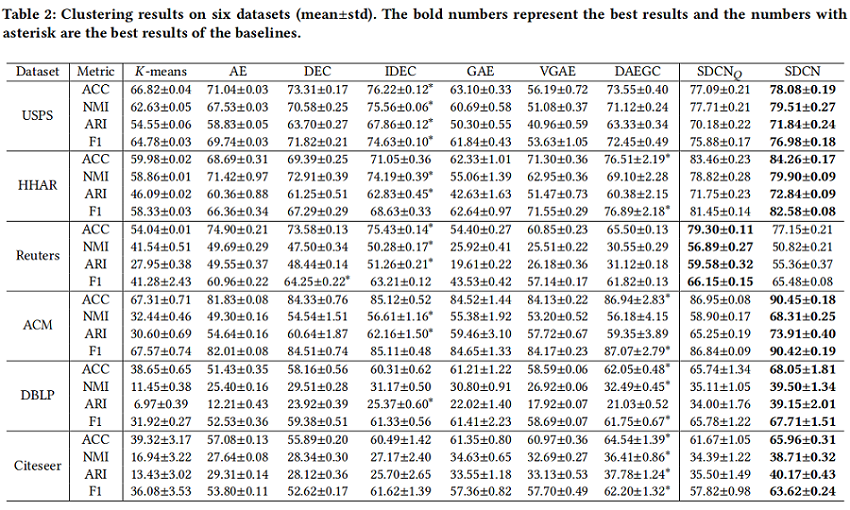
$SDCN_{Q}$ : 利用 $Q$ 软聚类做输出;
$SDCN$: 利用 $Z$ 软聚类做输出;
模型分析
验证GCN在学习结构信息方面的能力和传递算子(delivery operator)的生态能力:
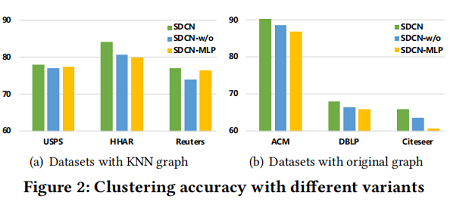
- SDCN-w/o: 不使用传递算子
- SDCN-MLP: 将GCN代替为MLP
传递层数影响
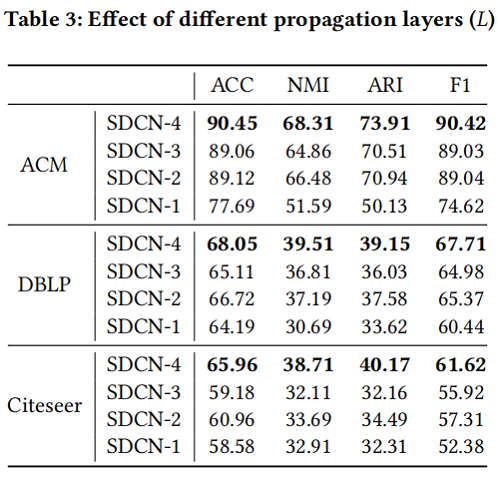
平衡系数 ϵ 研究
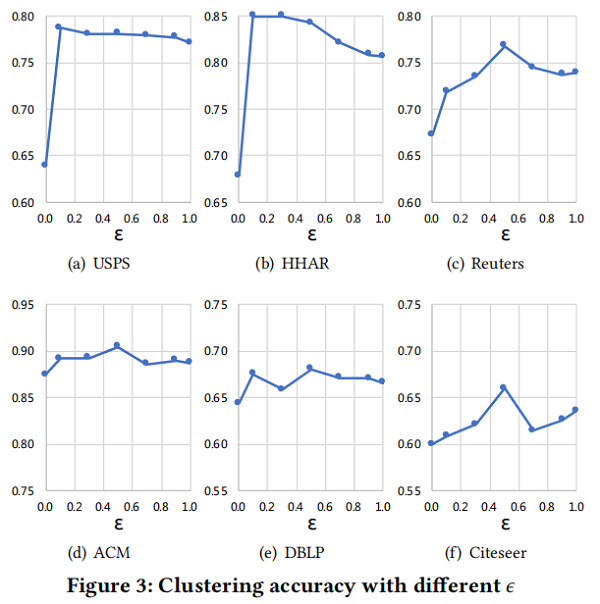
K 值敏感分析
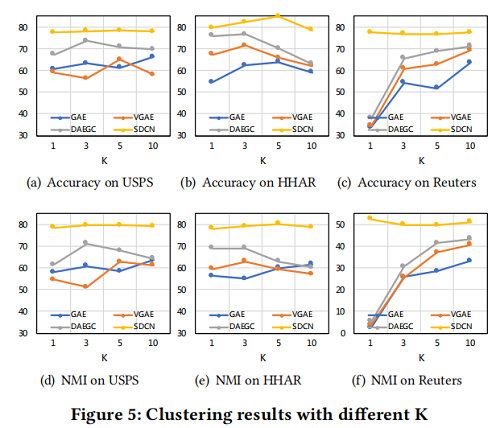
训练过程分析
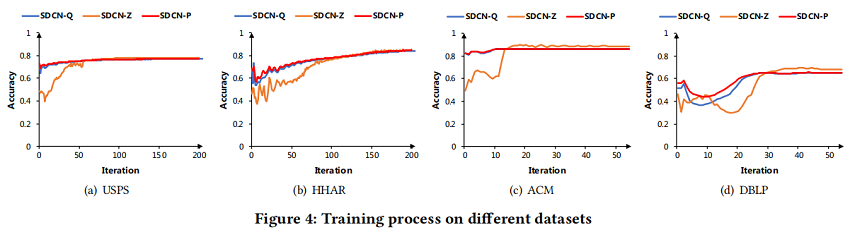
4 Conclusion
提出双自监督模块,将GCN 和 DNN 模型表示融合起来。
修改l历史
2021-12-25 创建文章
2022-06-08 切换到中文版本
因上求缘,果上努力~~~~ 作者:图神经网络,转载请注明原文链接:https://www.cnblogs.com/BlairGrowing/p/15723961.html


