性能度量

　　性能度量

　　　　对于分类任务，错误率和精度是最常用的两种性能度量：

• • • 错误率：分错样本占样本总数的比例
    • 精度：分对样本占样本总数的比率

　　错误率（error rate ）

　　　　　　$E(f ; D)=\frac{1}{m} \sum \limits _{i=1}^{m} \mathbb{I}\left(f\left(\boldsymbol{x}_{i}\right) \neq y_{i}\right)$

　　精度（ accuracy ）

　　　　　　$\begin{aligned}\operatorname{acc}(f ; D) &=\frac{1}{m} \sum \limits _{i=1}^{m} \mathbb{I}\left(f\left(\boldsymbol{x}_{i}\right)=y_{i}\right) \\&=1-E(f ; D)\end{aligned}$

　　Confusion Matrix

　　　　统计真实标记和预测结果的组合可以得到“混淆矩阵”：

　　　　　　　　

　　　　　　　　　　　　 

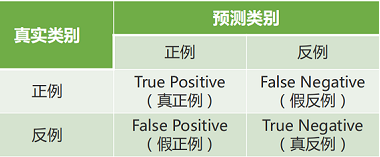
　　准确率 (Accuracy )

　　　　　　$ACC = \frac{T P+T N}{T P+T N+F P+F N}$

　　　　预测正确的结果占总样本的百分比 

　　y_pred = [0, 2, 1, 2]

　　y_true = [0, 1, 2, 3]

　　print(accuracy_score(y_true, y_pred))  # 0.25

　　4个样本，就第一个预测正确，所以准确率为 0.25。

　　查准率 ( Precision ) 

　　　　　　$ P= \frac{T P}{TP+F P}$   

　　　　即：对每一类     (好瓜)/（好瓜加坏瓜）

　　y_true = [0, 1, 2, 0, 1, 2]

　　y_pred = [0, 2, 1, 0, 0, 1]

　　对于第 0 类，y_true 两个 0，y_pred 三个 0， y_pred 三 个 0 都预测正确 2 个，所以查准率为2/3；

　　对于第 1 类，y_true 两个 1，y_pred 两个 1， y_pred 两 个 1 都预测错误，所以查准率为0；

　　对于第 2 类，y_true 两个 2，y_pred 一个 2， y_pred 一 个 2 都预测错误，所以查准率为0；

　　查全率/召回率/敏感度 ( Recall/Sensitivity )

　　　　　　$\frac{T P}{T P+F N} $

　　P-R曲线

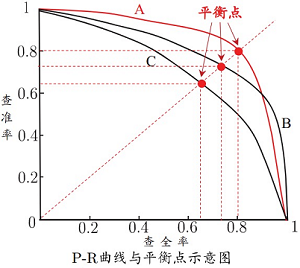
• • 若一个学习算法的PR曲线被另一个学习算法的曲线完全“包住”，则可认为后者的性能优于前者，如A优于C；
  • 若两个学习算法的PR曲线发生交叉（如A和B），则难以判断孰优孰劣，只能在具体的查准率和查全率条件下进行比较；
    • 可通过比较P-R曲线下的面积（PR-AUC）
    • 利用平衡点（即P=R时的取值）
    • 利用F1度量

　　　　　　　　

　　比P-R曲线平衡点更用常用的是F1度量： 

　　　　　　$F 1=\frac{2 \times P \times R}{P+R}=\frac{2 \times T P}{\text { 样例总数 }+T P-T N}$

　　比F1更一般的形式   $F_{\beta}$  度量: 

　　　　$ \beta=1$: 标准F1
　　　　$\beta>1 $: 偏重查全率(逃犯信息检索)
　　　　$  \beta<1$  : 偏重查准率(商品推荐系统)

　　宏平均

　　　　是先对每一个类统计指标值，然后在对所有类求算术平均值。

　　　　　　$\begin{aligned}macro-P &=\frac{1}{n} \sum \limits _{i=1}^{n} P_{i} \\macro -R &=\frac{1}{n} \sum \limits _{i=1}^{n} R_{i} \\macro -F1 &=\frac{2 \times macro-P \times macro-R}{macro-P+macro-R}\end{aligned}$

　　微平均

　　　　是对数据集中的每一个实例不分类别进行统计建立全局混淆矩阵，然后计算相应指标。

　　　　　　$\begin{array}{l}\text { micro }-P=\frac{\overline{T P}}{\overline{T P}+\overline{F P}} \\\text { micro }-R=\frac{\overline{T P}}{\overline{T P}+\overline{F N}} \\\text { micro }-F 1=\frac{2 \times \text { micro }-P \times \text { micro }-R}{\text { micro }-P+\text { micro }-R}\end{array}$

　　宏平均 vs 微平均

　　　　Macro-averaging vs. Micro-averaging

• • • l Macro-averaged gives equal weight to each class
    • l Micro-averaged gives equal weight to each per-instance classification decision
    • l Macro-averaging is a good choice when you get a sense of effectiveness on small classes
    • l Micro-averaging is a good choice on the large classes because large classes dominate small classes in micro-averaging
    • l Macro-averaging evaluates the system performance overall across the sets of data, can not get any specific decision with it
    • l Micro-average can be a useful measure when the dataset varies in size

　　真正率 & 假正率

　　　　真正率 (TPR ) = 灵敏度/召回率 = $\mathrm{TP} /(\mathrm{TP}+\mathrm{FN}) $ 正例中有多少样本被检测出
　　　　假正率 (FPR ) = 1- 特异度 = $\mathrm{FP} /(\mathrm{FP}+\mathrm{TN}) $ 负例中有多少样本被错误覆盖
　　　　　　　　

　　　　　　　　

　　　　所以无论样本是否平衡，都不会被影响。

　　ROC与AUC

　　　　ROC（Receiver Operating Characteristic）曲线，又称接受者操作特征曲线。该曲线最早应用于雷达信号检测领域，用于区分信号与噪声。后来人们将其用于评价模型的预测能力，ROC 曲线是基于混淆矩阵得出的。

　　如何绘制ROC曲线？

　　　　与前面的 P-R 曲线类似，ROC 曲线也是通过遍历所有阈值 来绘制整条曲线如果我们不断的遍历所有阈值，预测的正样本和负样本是在不断变化的，相应的在 ROC 曲线图中也会沿着曲线滑动。

　　　　　　　　

　　若某个学习器的ROC曲线被另一个学习器的曲线“包住”，则后者性能优于前者；

　　否则如果曲线交叉，可以根据ROC曲线下面积大小进行比较，也即AUC值.

　　　　　　

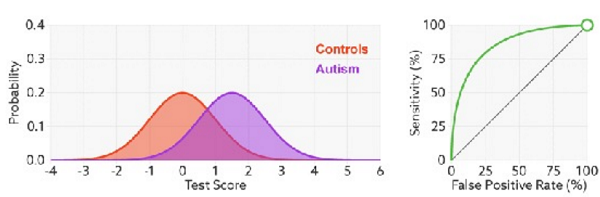
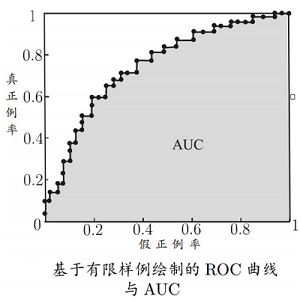
　　　　假设ROC曲线由 $\left\{\left(x_{i}, y_{i}\right)\right\}_{i=1}^{m}$ 的点按序连接而 形成 $\left(x_{1}=0, x_{m}=1\right)$ 则 $A \cup C$ 可估算为 :

　　　　　　$\mathrm{AUC}=\frac{1}{2} \sum_{i=1}^{m-1}\left(x_{i+1}-x_{i}\right) \cdot\left(y_{i}+y_{i+1}\right)$

　　　　AUC衡量了样本预测的排序质量。

　　代价敏感错误率

　　　　现实任务中不同类型的错误所造成的后果很可能不同，为了权衡不同类型错误所造成的不同损失，可为错误赋予“非均等代价”。

　　　　以二分类为例，可根据领域知识设定 "代价矩阵" ，如下表所示，其中  $\cos t_{i j}$  表示将第 $i$ 类样本预测为第 $j$ 类样本的代价。损失程度越大， $cost  _{01}$  与  $\operatorname{cost}_{10}$  值的差别越大。

　　　　　　　　

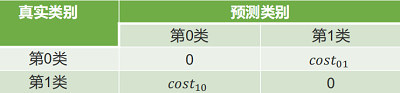
　　　　在非均等代价下，不再最小化错误次数，而是最小化“总体代价”，则“代价敏感”错误率相应的为：

　　　　　　$E(f ; D ; \operatorname{cost})=\frac{1}{m}\left(\sum \limits _{x_{i} \in D^{+}} \mathbb{I}\left(f\left(x_{i}\right) \neq y_{i}\right) \times \operatorname{cost}_{01}+\sum \limits_{x_{i} \in D^{-}} \mathbb{I}\left(f\left(x_{i}\right) \neq y_{i}\right) \times \operatorname{cost}_{10}\right)$

　　代价曲线

　　　　在非均等代价下，ROC曲线不能直接反映出学习器的期望总体代价，而“代价曲线”可以。

　　　　代价曲线的横轴是取值为[0,1]的正例概率代价

　　　　　　$P(+) \operatorname{cost}=\frac{p \times \cos t_{01}}{p \times \operatorname{cost}_{01}+(1-p) \times \operatorname{cost}_{10}}$

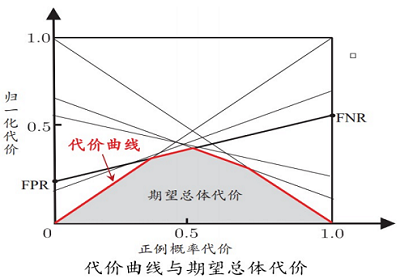
　　　　纵轴是取值为 $[0,1] $ 的归一化代价

　　　　　　$\operatorname{cost}_{n o r m}=\frac{\text { FNR } \times p \times \operatorname{cost}_{01}+\text { FPR } \times(1-p) \times \operatorname{cost}_{10}}{p \times \operatorname{cost}_{01}+(1-p) \times \operatorname{cost}_{10}}$

　　　　代价曲线图的绘制：ROC曲线上每个点对应了代价曲线上的一条线段，设ROC曲线上点的坐标为(TPR,FPR),则可相应计算出FNR,然后在代价平面上绘制一条从(0,FPR)到(1,FNR)的线段，线段下的面积即表示了该条件下的期望总体代价；如此将ROC曲线上的每个点转化为代价平面上的一条线段，然后取所有线段的下界，围成的面积即为所有条件下学习器的期望总体代价。

　　　　　　

 

 『总结不易，加个关注呗！』