论文解读(node2vec)《node2vec Scalable Feature Learning for Networks》
论文信息
论文标题:node2vec: Scalable Feature Learning for Networks
论文作者:Aditya Grover, Jure Leskovec
论文来源:2016,KDD
论文地址:download
论文代码:download
1 Introduction
1.1 Review Deepwalk
Graph embedding:
-
- 基于 手工构造特征;
- 基于 矩阵分解【邻接矩阵】;
- 基于 随机游走;
- 基于 图神经网络;
回顾一下 DeepWalk :
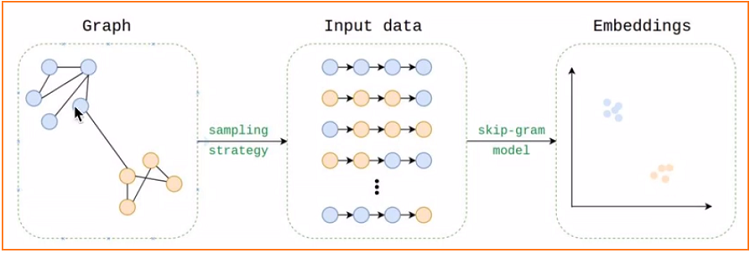
从图中采样一系列的随机游走序列,用中心节点预测相邻节点,目的是使得相邻节点嵌入尽可能相似。
DeepWalk 的缺点:
-
- 用完全随机游走,训练节点表示向量;
- 仅能反映相邻节点的社群相似信息;
- 无法反应节点角色相似信息;【node2vec 要解决的问题】
1.2 Main body
-
- 同一个 ”社区“ 的节点嵌入尽可能相似;【$s_1$ 和 $u$】
- 在 “社区” 中扮演相同角色的节点嵌入也尽可能相似;【$u$ 和 $s_6$】
-
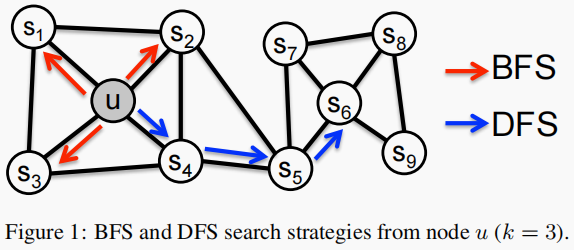
- 在 BFS 中,采样邻域中的节点倾向于重复很多次,它减少了描述 1 跳节点相对于源节点的分布的方差。然而,对于任何给定的 $k$,只探索了图的一小部分。【微观角度】
- 在 DFS 中,它可以探索网络的更大部分,因为它可以采样远离源节点 $u$ 的节点(样本大小 $k$ 是固定的)。【宏观角度】
DFS:邻域被限制为源的近邻节点。
在 Figure 1 中,假设 $k=3$, 则在 $u$ 的附近采样 node $s_{1}, s_{2}, s_{3}$。
BFS:邻域由距离源节点的距离顺序采样的节点组成。
在 Figure 1 中,假设 $k=3$, 则在 $u$ 的某路径上采样 node $s_{4}, s_{5}, s_{6}$。
2 Feature learning framework
Skip-gram architecture 的目标函数:
$\underset{f}{max} \quad \sum \limits _{u \in V} \log \operatorname{Pr}\left(N_{S}(u) \mid f(u)\right) \quad \quad \quad \quad (1)$
即:用中心节点预测邻居节点。【$f: V \rightarrow \mathbb{R}^{d}$ 】
且满足
-
- 条件独立
-
- 特征空间中的对称性
$\operatorname{Pr}\left(n_{i} \mid f(u)\right)=\frac{\exp \left(f\left(n_{i}\right) \cdot f(u)\right)}{\sum\limits_{v \in V} \exp (f(v) \cdot f(u))}$
根据上述两条件得:
$\underset{f}{\text{max}}\sum \limits_{u \in V}\left[-\log Z_{u}+\sum\limits_{n_{i} \in N_{S}(u)} f\left(n_{i}\right) \cdot f(u)\right]$
其中 $Z_{u}=\sum \limits _{v \in V} \exp (f(u) \cdot f(v))$ 。
推导过程:
$\begin{array}{l}\underset{f}{max} \sum \limits _{u \in V} \log P_{r}\left(N_{s}(u) \mid f(u)\right)\\\left.=\underset{f}{max} \sum \limits _{u \in V} \log \prod \limits_{n_{i} \in N_{s}(u)} P_{r}\left(n_{i}\right) f(u)\right)\\=\underset{f}{max} \sum \limits_{u \in V} \sum \limits_{n_{i} \in N_{s}(u)} \log \frac{\operatorname{exp}\left(f\left(n_{i}\right) \cdot f(u)\right)}{\sum \limits_{v \in V} \exp (f(v) \cdot f(u))}\\=\underset{f}{max} \sum \limits _{u \in V}\left[-\sum \limits_{n_{i} \in N_{s}(u)} \log Z_{u}+\sum \limits_{n_{i} \in N_{s}(u)} f\left(n_{i}\right) f(u)\right]\\=\underset{f}{max} \sum \limits _{u \in V}\left[-\left|N_{s}(u)\right| \log Z_{u}+\sum \limits_{n_{i} \in N_{s}(u)} f\left(n_{i}\right) f(u)\right]\end{array} $
Note:推导中的常数 $\left|N_{s}(u)\right|$ 被忽略掉了,因为对于 $Z_{u}$ 使用了负采样策略,和邻居节点没有关系,计算 $\left|N_{s}(u)\right|$ 显得没必要。
3 node2vec
平滑地在 BFS 和 DFS 之间进行插值,实现 biased random walk 来探索图。
3.1 Random Walks
给定一个源节点 $u$ ,模拟一个固定长度为 $l$ 的随机游走。设 $c_i$ 表示行走中的第 $i$ 个节点,以 $c_0=u$ 开始。节点 $c_i$ 由以下分布方式生成:
$P\left(c_{i}=x \mid c_{i-1}=v\right)=\left\{\begin{array}{ll}\frac{\pi_{v x}}{Z} & \text { if }(v, x) \in E \\0 & \text { otherwise } \end{array}\right.$
其中 $\pi_{v x}$ 为节点 $v$ 和节点 $x$ 之间的非标准化的转移概率,$Z$ 为归一化常数。
3.2 Search bias α
对于 $\pi_{v x}=w_{v x}$ :
-
- 无权图设置 $w_{v x} = 1$
- 有权图设置 $\pi_{v x}=w_{v x}$
直接使用上述 $\pi_{v x}$ 又回到了 DeepWalk ,而使用 BFS 和 DGS 又过于极端,因此本文定义了一个具有两个参数 $p$ 和 $q$ 的二阶随机游走:
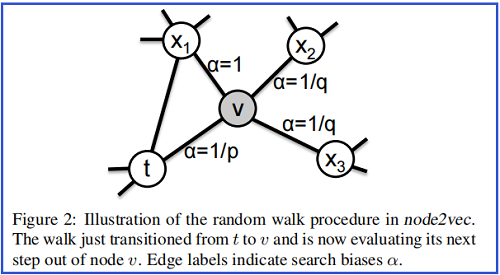
已采样 $(t,v)$ ,即现在停留在节点 $v$ 上,下一个要采样的节点假设为 $\mathrm{x}$,采样 $\mathrm{x}$ 的转移概率为:
$\pi_{v x}=\alpha_{p q}(t, x) \cdot w_{v x}$
其中:
$\alpha_{p q}(t, x)=\left\{\begin{array}{ll}\frac{1}{p} & \text { if } d_{t x}=0 \\1 & \text { if } d_{t x}=1 \\\frac{1}{q} & \text { if } d_{t x}=2\end{array}\right.$
$d_{tx}$ 表示节点 $t$ 和节点 $x$ 之间的最短路径距离。
$\alpha_{p q}(t, x)$ 解释如下:
-
- 采样 $\mathrm{x}$ 的概率为 $\frac{1}{p} $,即 返回 到上一步的节点 $t$ ;【考虑自身,缓解过平滑问题】
- 采样 $\mathrm{x}$ 的概率 $1$ ,即 徘徊到 $t$ 的一阶邻居;【BFS】
- 采样 $\mathrm{x}$ 概率为 $\frac{1}{q} $,即 远行 到 $t$ 的二阶邻居;【DFS】
参数 $p、q $ 的意义分别如下:
Return parameter p:【返回】
-
- 如果 $p>max(q,1)$,采样会尽量不往回走,即:下一个节点不太可能是上一个访问的节点 $t$ ;
- 如果 $p<min(q,1)$,采样会尽量往回走,即:下一个节点太可能是上一个访问的节点 $t$ ;
意义:主要在某个节点周围采样。
In-out parameter q:【DFS & BFS】
-
- 如果 $q>1$ ,那么游走会倾向于在起始点周围的节点之间跑,反映 BFS 特性;
- 如果 $q<1$ ,那么游走会倾向于往远处跑,反映出 DFS 特性;
当 $p=1,q=1$ 时,游走方式就等同于 DeepWalk 中的随机游走。
复杂度:
-
- 空间复杂度:二阶随机游走的空间复杂度为 $O\left(a^{2}|V|\right)$,其中 $a$ 代表了平均度;
- 时间复杂度:$O(\frac{l}{k(l-k)} = \frac{1}{k}-\frac{1}{l-k})$,其中 $l$ 为随机游走长度,$k$ 为根节点的邻居数,大致意思为 $l$ 越大,根节点被采样的概率越大;
3.3 The node2vec algorithm

其中 ,$\pi=\text { PreprocessModifiedWeights }(G, p, q)$ 为生成随机游走策略,AliasSample 的采样时间复杂度为 $O(1)$。
上述算法的优势:可以并行。
Note:AliasSample 用连续数据模拟离散采样。

3.2 Learning edge features
即 链接预测(link prediction):

4 Experiments
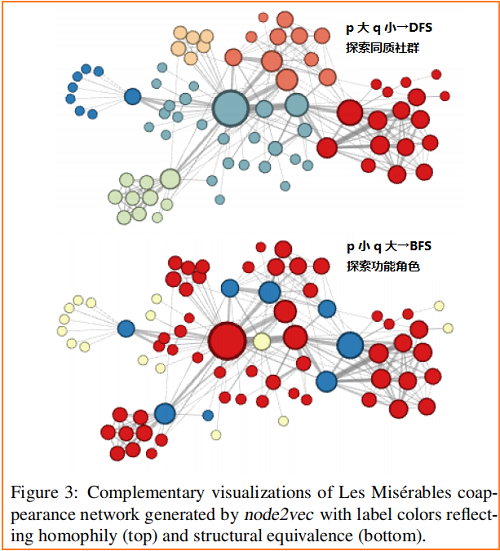
4.1 Case Study: Les Misérables network
《悲惨世界》人物关系图:
4.2 Experimental setup
节点分类:
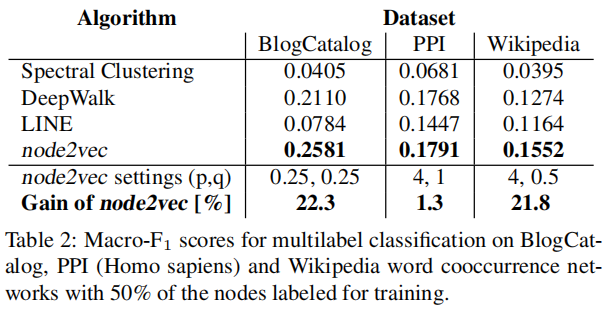
报告的结果是:10个随机种子 的平均结果。【大部分的论文一般都是固定随机种子】
研究数据划分的影响:将 train-test split 从 $10\%$ 改变到 $90\%$
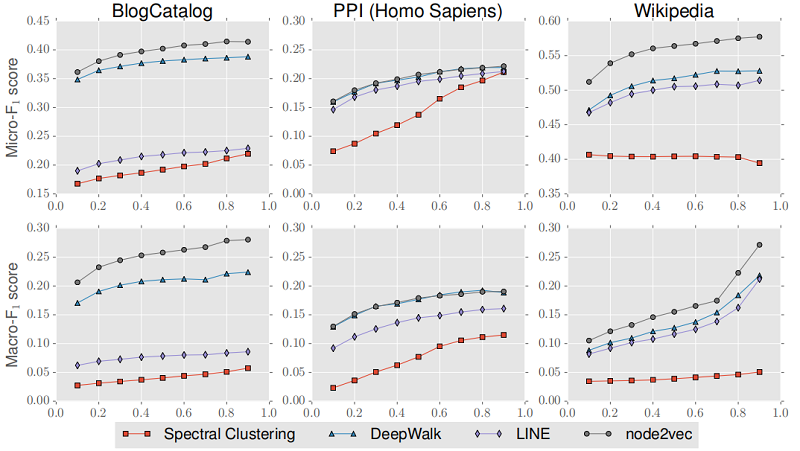
4.4 Parameter sensitivity
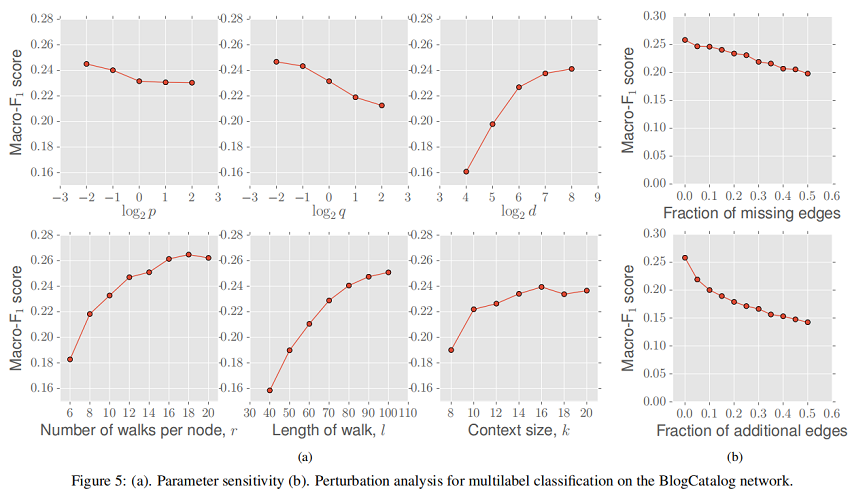
4.5 Perturbation Analysis
研究 missing edges 对性能的影响,缺失边是随机选择的。在 Figure 5 b(top)中看到,随着缺边比列的增加,Macro-F1 分数大致呈线性下降,斜率较小。在图随着时间的推移而演化(例如引文网络)或网络构建昂贵(例如生物网络)时,对网络中缺失边缘的鲁棒性尤为重要。
研究 additional edge 对性能的影响。node2vec 的性能最初下降的速度略快,但Macro-F1评分的下降速度随着时间的推移逐渐减慢。同样,node2vec 对 false edges 的鲁棒性在一些情况下是有用的,如传感器网络,用于构建网络的测量值是有噪声的。
4.6 Scalability
采样节点从 100 个节点到 1000,000 个节点,平均度设置为10 不变 ,实验如下:
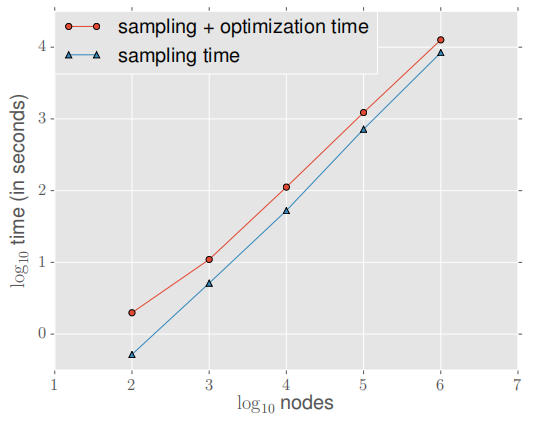
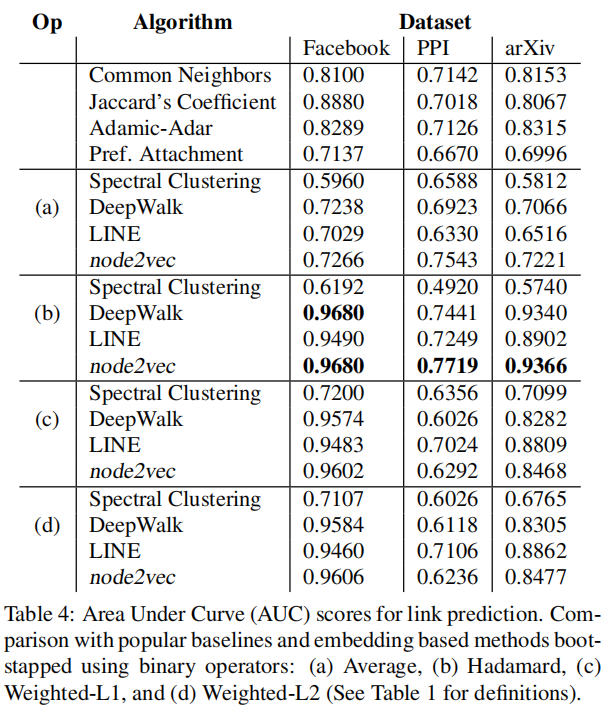
4.7 Link prediction
随机删除 50% 的边,根据学习到的表示预测边,然后计算 Link prediction heuristic score :

实验结果:
5 Conclusion
主要用于反映角色功能。
修改历史
2021-11-26 创建文章
2022-08-05 精度论文
因上求缘,果上努力~~~~ 作者:图神经网络,转载请注明原文链接:https://www.cnblogs.com/BlairGrowing/p/15601261.html


