论文解读(LINE)《LINE: Large-scale Information Network Embedding》
论文信息
论文标题:LINE: Large-scale Information Network Embedding
论文作者:Jian Tang, Meng Qu , Mingzhe Wang, Ming Zhang, Jun Yan, Qiaozhu Mei
论文来源:2015, WWW
论文地址:download
论文代码:download
1 Introduction
本文提出一种同时考虑局部和全局信息的框架,同时适用于无向图、有向图。
举例:朋友关系网络
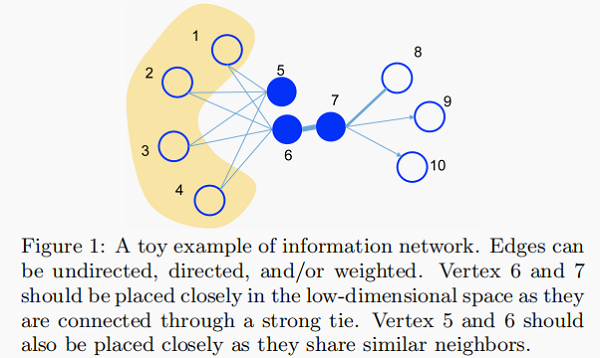
Figure 1 给出了一个说明性的例子。由于顶点 6 和 7 之间的边的权重很大,即 6 和 7 的一阶(first-order)接近,因此在嵌入空间中应紧密表示。另一方面,虽然顶点 5 和顶 6 之间没有联系,但它们共享许多共同的邻居,即它们具有很高的二阶接近性,因此也应相互紧密地表示。
总结:考虑直接关系和相同局部结构。
2 Definition
Definition 2 . (First-order Proximity) The first-order proximity in a network is the local pairwise proximity between two vertices. For each pair of vertices linked by an edge $(u, v)$ , the weight on that edge, $w_{u v}$ , indicates the firstorder proximity between $u $ and $v$ . If no edge is observed between $u$ and $v$ , their first-order proximity is $0$ .
如 Figure 1 ,6 和 7 之间存在直连边,且边权较大,则认为两者相似且 1 阶相似度较高,而 5 和 6 之间不存在直连边,则两者间 1 阶相似度为 0。
现实世界中,直接相连的边比较缺乏(缺个棒槌),所以可以考虑局部结构,因此引入了二阶接近度。
Definition 3. (Second-order Proximity) The secondorder proximity between a pair of vertices $(u, v)$ in a network is the similarity between their neighborhood network structures. Mathematically, let $p_{u}=\left(w_{u, 1}, \ldots, w_{u,|V|}\right)$ denote the first-order proximity of $u$ with all the other vertices, then the second-order proximity between $u$ and $v$ is determined by the similarity between $p_{u}$ and $p_{v}$ . If no vertex is linked from/to both $u$ and $v$ , the second-order proximity between $u$ and $v$ is $0$ .
如 Figure 1 ,虽然 5 和 6 之间不存在直连边,但是他们有很多相同的邻居顶点 $(1,2,3,4)$,这其实也可以表明5和6是相似的,而 $2$ 阶相似度就是用来描述这种关系的。
3 Method
3.1 LINE with First-order Proximity
每条无向边 $(i、j)$,顶点 $v_i$ 和 $v_j$ 之间的联合概率如下:
${\large p_{1}\left(v_{i}, v_{j}\right)=\frac{1}{1+\exp \left(-\vec{u}_{i}^{T} \cdot \vec{u}_{j}\right)}} $
其中 $\vec{u}_{i} \in R^{d}$ 为顶点 $v_i$ 的低维向量表示。
顶点 $v_i$ 和 $v_j$ 之间经验概率为
$\hat{p}_{1}(i, j)=\frac{w_{i j}}{W} $
其中 $W=\sum_{(i, j) \in E} w_{i j}$ 。
优化目标如下:
$O_{1}=d\left(\hat{p}_{1}(\cdot, \cdot), p_{1}(\cdot, \cdot)\right)$
其中 $d(·,·)$ 为两个分布之间的距离,本文选择 KL 散度衡量分布之间的距离。
忽略 KL 散度中的常数项后有:
$O_{1}=-\sum_{(i, j) \in E} w_{i j} \log p_{1}\left(v_{i}, v_{j}\right)$
注意:一阶接近度只适用于无向图,而不适用于有向图。
3.2 LINE with Second-order Proximity
局部结构可以认为是顶点的上下文(Context),并常假设上下文相似的节点,其节点也相似,二阶接近度的出发点也是如此。
引入两个向量 $ \vec{u}_{i}$ 和 $\vec{u}_{i}^{\prime} $,其中 $ \vec{u}_{i}$ 代表 $v_i$ 的表示,而 $\vec{u}_{i}^{\prime} $ 代表 $v_i$ “上下文” 的表示。对于每个有向边 $(i、j)$,将顶点 $v_i$ 生成 “上下文” $v_j$ 的概率定义为:
${\large p_{2}\left(v_{j} \mid v_{i}\right)=\frac{\exp \left(\vec{u}_{j}^{T} \cdot \vec{u}_{i}\right)}{\sum_{k=1}^{|V|} \exp \left(\vec{u}_{k}^{\prime T} \cdot \vec{u}_{i}\right)}} $
其中,$|V|$ 是“上下文”的数量。
二阶接近度的经验分布 $\hat{p}_{2}\left(\cdot \mid v_{i}\right)$:
$\hat{p}_{2}\left(v_{j} \mid v_{i}\right)=\frac{w_{i j}}{d_{i}}$
其中,$d_i$ 是顶点 $i$ 的出度,即 $d_{i}=\sum _{k \in N(i)} w_{i k}$ ,$N(i)$ 是 $v_i$ 的邻居集合。
同理,二阶接近度最小化以下目标函数:
$O_{2}=\sum \limits _{i \in V} \lambda_{i} d\left(\hat{p}_{2}\left(\cdot \mid v_{i}\right), p_{2}\left(\cdot \mid v_{i}\right)\right)$
为简单,设置 $λ_i=d_i$ 并省略一些常数,有:
$O_{2}=-\sum \limits _{(i, j) \in E} w_{i j} \log p_{2}\left(v_{j} \mid v_{i}\right)$
注意:二阶接近度适用于无向图,也适用于有向图。
3.3 Model Optimization
由于优化 $O_2$ 的计算代价很高(需要对整个顶点集处理),为解决这个问题,本文提出负采样策略优化目标函数:
$\log \sigma\left(\vec{u}_{j}^{T} \cdot \vec{u}_{i}\right)+\sum \limits _{i=1}^{K} E_{v_{n} \sim P_{n}(v)}\left[\log \sigma\left(-\vec{u}_{n}^{\prime T} \cdot \vec{u}_{i}\right)\right]$
其中,
-
- $σ(x)=1/(1+exp(−x))$ 为 Sigmoid 函数;
- $K$ 是负边的个数;
- $P_{n}(v) \propto d_{v}^{3 / 4}$ ;
采用异步随机梯度算法(ASGD)进行优化。在每一步中,ASGD算法对一批边进行采样,然后更新模型参数。如果对一条边 $(i、j)$ 进行采样,则采用顶点 $i$ 的嵌入向量 $\vec{u}_{i}$ 的梯度将计算为:
$\frac{\partial O_{2}}{\partial \vec{u}_{i}}=w_{i j} \cdot \frac{\partial \log p_{2}\left(v_{j} \mid v_{i}\right)}{\partial \vec{u}_{i}}$
请注意,梯度将乘以边的权重。当边的权值具有高方差时,这就会成为问题。
例如,在一个单词共发生网络中,一些单词同时出现很多次,而有些单词只同时出现几次。在这样的网络中,梯度的尺度会发散,很难找到一个好的学习率。如果根据权值小的边选择较大的学习率,权值大的边上的梯度会爆炸,而如果根据权值大的边选择学习率,梯度会太小。
3.4 Optimization via Edge Sampling
上述权值问题对于图中边权重相同时(0 或 1)不存在问题。
一种简单的解决方法是将权重为 $w$ 的边展开为 $w$ 个 二元边(0、1),然后根据其权重作为采样概率进行采样,但是带来的问题是内存消耗大。
另一种做法是:令 $W = (w_1, w_2, ... , w_{|E|}) $ 表示边的权重。 首先计算权重总和 $w_{sum} = = \sum_{i=1}^{|E|}w_{i}$ ,然后采样 $[0, w_{sum}]$ 范围内的随机值,查看随机值属于哪个区间 $[\sum_{j=0}^{i-1}w_{j}, \sum_{j=0}^{i}w_{j})$ 。 这个 方法需要 $O(|E|) $ 时间来抽取样本,当边数 $|E| $ 很大这是昂贵的。
本文是采用别名表进行采样,从别名表中采样一条边需要恒定的时间 $O(1) $ ,而使用负采样的优化需要 $O(d(K+1))$ 时间,其中 $K$ 为负样本的数量。因此,总体上,每个步骤都需要 $O(dK)$ 时间。
在实践中,我们发现用于优化的步骤数通常与边数 $O(|E|)$ 成正比。因此,LINE 的总体时间复杂度为 $O(dK|E|)$ ,它与边数 $|E|$ 呈线性关系,而不依赖于顶点数 $|V|$ 。边缘采样处理提高了随机梯度下降的有效性,而不降低了效率。
3.5 Discussion
- Low degree vertices:如何准确地嵌入小度的顶点。
由于这种节点的邻居数量非常少,很难准确地推断出其表示,特别是基于二阶接近的方法,它严重依赖于 “上下文” 的数量。一个直观的解决方案是通过添加更高阶的邻居来扩展这些顶点的邻居,比如邻居的邻居。在本文中,我们只考虑向每个顶点添加二阶邻居,即邻居的邻居。顶点 $i$ 与其二阶邻域 $j$ 之间的权重被测量为
$w_{i j}=\sum \limits _{k \in N(i)} w_{i k} \frac{w_{k j}}{d_{k}}$
实际上,只添加一个顶点集 ${j}$,它们具有最大的顶点子集。
- New vertices:如何找到新到达的顶点的表示。
对于一个新的顶点 $i$,如果它与现有顶点的边连接关系已知,可以得到现有顶点上的经验分布 $\hat{p}_{1}\left(\cdot, v_{i}\right)$ 和 $\hat{p}_{2}\left(\cdot \mid v_{i}\right)$。根据目标函数 $O_1$ 或者 $O_2$,得到新顶点的嵌入。一种简单的方法是最小化以下目标函数之一
$-\sum \limits _{j \in N(i)} w_{j i} \log p_{1}\left(v_{j}, v_{i}\right), \text { or }-\sum \limits_{j \in N(i)} w_{j i} \log p_{2}\left(v_{j} \mid v_{i}\right)$
通过更新新顶点的嵌入和保持现有顶点的嵌入。如果没有观察到新顶点和现有顶点之间的连接,我们必须求助于其他信息,如顶点的文本信息,并将其留给我们未来的工作。
4 Experiments
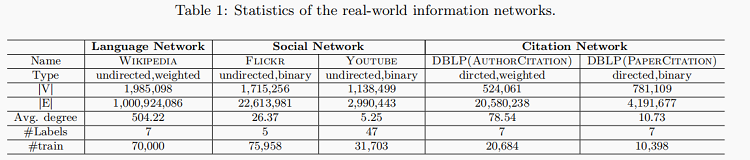
数据集
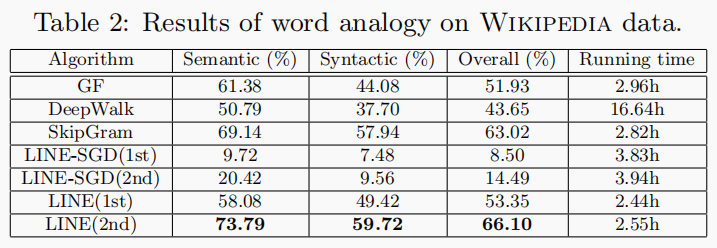
文档分类
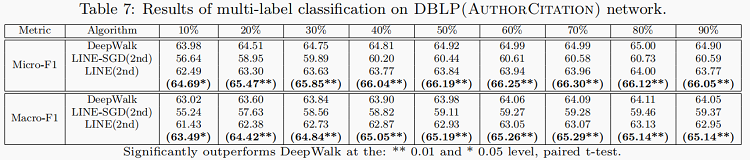
多标签分类



可视化

5 Conclusion
LINE模型具有精心设计的客观功能,保留了一阶和二阶接近度,相互互补。并提出了一种有效和有效的边缘抽样方法进行模型推理;解决了加权边缘随机梯度下降的限制,而不影响效率。此外,除一阶和二阶之外更高的相似度也是LINE模型算法在未来能够更加拓宽的方面。异构网络的嵌入,也是研究的方向之一。
修改历史
2021-11-18 创建文章
2022-06-07 修订文章
因上求缘,果上努力~~~~ 作者:别关注我了,私信我吧,转载请注明原文链接:https://www.cnblogs.com/BlairGrowing/p/15552024.html


 浙公网安备 33010602011771号
浙公网安备 33010602011771号