邻接矩阵的相乘的意义

假设一个$N$个结点的无向图
我们用 $G[u][v]=G[v][u]=1$ 表示 $ u$ 到 $ v$ 有连边， 否则 $ G[u][v]=G[v][u]=0 $
如果用这个邻接矩阵自乘会得到什么呢
模拟矩乘的运算有 $ G^{2}[u][v]=\sum \limits_{i=1}^{n} G[u][i] * G[i][v]$ 也就是说 $ G^{2}[u][v]$ 是表示图上 $ u$ 到 $ v$ 恰好经过两条边的路径的条数的矩阵

我们可以把原始邻接矩阵 G[u][v] 看作为
表示图上 $ u$ 到 $ v$ 恰好经过一条边的路径条数的矩阵 那么 $ G^{2}[u][v]=\sum \limits_{i=1}^{n} G[u][i] * G[i][v]$ 显然就是运用了乘法原理与加法原理
再考虑 $ G^{3}[u][v]$ 呢
由 $ G^{3}$ 的计算过程 $ G^{3}[u][v]=\sum_{i=1}^{n} \sum \limits_{j=1}^{n} G[u][i] * G[i][j] * G[j][v]$ 同理可知其表示为图上 $ u$ 到 $ v$ 恰好经过三条边的路径条数的矩阵 或者我们也可以将其看作 $ G^{3}=G^{2} * G$ 理解，其本质是相同的
由上述不难发现该性质对于一般的正整数k都是成立的
即 $ G^{k}[u][v]$ 是表示图上 $ u$ 到 $ v$ 恰好经过 $K$ 条边的路径条数的矩阵
也就是说
如果需要在某个图上求 $ u$ 到 $ v$ 恰好经过$ K$ 条边的路径的条数 我们完全可以使用矩阵快速帛来优化这个计算过程
当然，这个性质对于有向图以及有重边的图同样适用 对于有重边的图，把初始矩阵 $ G[u][v]$ 改成记录 $ u, v$ 之前边的条数即可

 

Example

　　　　

 

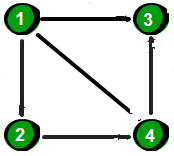
a=[
    [0,1,1,1],
    [1,0,0,1],
    [1,0,0,1],
    [1,1,1,0],
]
A = torch.tensor(a)
torch.mm(A,A)
tensor([[3, 1, 1, 2],
        [1, 2, 2, 1],
        [1, 2, 2, 1],
        [2, 1, 1, 3]])

torch.mm(torch.mm(A,A),A)
tensor([[4, 5, 5, 5],
        [5, 2, 2, 5],
        [5, 2, 2, 5],
        [5, 5, 5, 4]])