论文解读（DeepWalk）《DeepWalk: Online Learning of Social Representations》

论文信息

论文标题：DeepWalk: Online Learning of Social Representations
论文作者：Bryan Perozzi、Rami Al-Rfou、Steven Skiena
论文来源：2014,KDD
论文地址：download
论文代码：download

1 Introduction

　　本文通过将已经成熟的自然语言处理模型word2vec应用到网络的表示上，做到了无需进行矩阵分解即可表示出网络中的节点的关系。

　　DeepWalk把图中节点进行的一串随机游走类比于 word2vec 中单词的上下文，作为 word2vec 算法的输入，进而把节点表示成向量。输出的结果能够被多种分类算法作为输入应用。

2 Random Walks

　　所谓随机游走(random walk)，就是在网络上不断重复地随机选择游走路径，最终形成一条贯穿网络的路径。从某个特定的端点开始，游走的每一步都从与当前节点相连的边中随机选择一条，沿着选定的边移动到下一个顶点，不断重复这个过程。

　　关于随机斿走的符号解释: 以 $v_{i}$ 为根节点生成的一条随机游走路径为 $W_{v_{i}} $ ，其中路径上的点分别标记为 $W_{v_{i}}^{1}, W_{v_{i}}^{2}, W_{v_{i}}^{3} \ldots$。

　　截断随机游走(truncated random walk)实际上就是长度固定的随机游走。

　　随机游走的两个好处：

- 并行化，随机游走是局部的，对于一个大的网络来说，可以同时在不同的顶点开始进行一定长度的随机游走，多个随机游走同时进行，可以减少采样的时间。
- 适应性，可以适应网络局部的变化。网络的演化通常是局部的点和边的变化，这样的变化只会对部分随机游走路径产生影响，因此在网络的演化过程中不需要每一次都重新计算整个网络的随机游走。

3 Connection: Power laws

　　使用随机游走的顶点，附近顶点分布满足 power-low 分布

4 Language Modeling

　　首先来看词向量模型：
　　　　$w_{i}^{u}=\left(w_{0}, w_{1}, w_{2}, \ldots, w_{n}\right)$ 是一个由若干单词组成的序列，其中 $w_{i} \in V( Vocabulary )$，$V$ 是词汇表，也就是所有单词组成的集合。
　　在整个训练集上需要优化的目标是:

　　　　$\operatorname{Pr}\left(w_{n} \mid w_{0}, w_{1}, \ldots, w_{n}-1\right)$

　　也就是给定 $w_0,w_1,.......,w_{i-1}$ 要求出下一个 $w_{i}$ 出现的概率

　　将语言模型中的单词映射到图表示上去，单词即对应了图中的节点 $v_i$ ，句子序列对应了网络中的随机游走，那么对于一个随机游走$v_0,v_1,v_2,.......,v_{i-1}$需要优化的目标是：

　　$\operatorname{Pr}\left(v_{i} \mid\left(v_{0}, v_{1}, \ldots, v_{i-1}\right)\right)$

　　按照上面的理解就是，当知道 $\left(v_{0}, v_{1}, \ldots, v_{i-1}\right)$ 游走路径后，游走的下一个节点是 $v_{i}$ 的概率是多少? 可是这里的 $v_{i}$ 是顶点本身没法计算，于是引入一个映射函数$\Phi$，它的功能是将顶点映射成向量，转化成向量后就可以对顶点 $v_{i}$ 进行计算了。

　　　　$\Phi: v \in V \mapsto \mathbb{R}^{|V| \times d}$

　　所以怎么计算这个概率呢？同样借用词向量中使用的 skip-gram 模型。

　　Skip-gram模型有这样3个特点：

- 不使用上下文 (context) 预测缺失词 (missing word)，而使用缺失词预测上下文。因为 $\left(\left(v_{0}\right),\left(v_{1}\right), \ldots,\left(v_{i}-1\right)\right)$ 这部分太难算了，但是如果只计算一个 $\left(v_{k}\right)$ 和左右 2 个窗口内的节点，其中 $v_{k}$ 是缺失词，这就很好算。
- 不考虑顺序，只要是窗口中出现的词都算进来，而不管它具体出现在窗口的哪个位置。

　　应用 Skip-gram 模型后，优化目标变成了这样：

　　　　$\underset{\Phi}{\operatorname{minimize}} \quad-\log \operatorname{Pr}\left(\left\{v_{i-w}, \cdots, v_{i-1}, v_{i+1}, \cdots, v_{i+w}\right\} \mid \Phi\left(v_{i}\right)\right)$

5 Algorithm: DeepWalk

　　整个 DeepWalk 算法包含两部分，一部分是随机游走的生成，另一部分是参数的更新。

　　随机游走的生成：随机游走生成器取一个图 $G$，并均匀地采样一个随机顶点 $v_i$ 作为随机游走$W_{v_i}$ 的根。从访问的最后一个顶点的邻居中均匀地采样，直到达到最大长度 $t$ 。

　　算法：

6 SkipGram

　　SkipGram是一种语言模型，它最大化句子中大小的窗口内出现的词的共现概率。算法2 展示了SkipGram在DeepWalk中的应用：

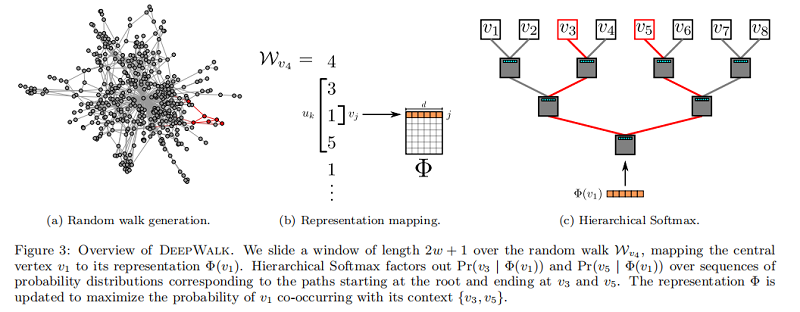
　　算法2 迭代出现在窗口 $w$（第1-2行）内的随机游走中的所有可能的组合。对于每个顶点，我们将每个顶点 $v_j$ 映射到它当前的表示向量$\Phi\left(v_{j}\right) \in \mathbb{R}^{d}$ (见图3b)。给定 $v_j$ 的表示，我们希望最大限度地提高其邻居在行走中的概率（第3行）。我们可以使用不同的分类器来学习这种后验分布。例如，使用逻辑回归建模前面的问题将导致大量的标签（约 $|V|$ ），可能是数百万或数十亿美元。这样的模型需要大量的计算资源，可以跨越整个计算机集群。为了加快训练时间，可以使用 Hierarchical Softmax 最大来近似概率分布。

7 Hierarchical Softmax

　　考虑到 $u_{k} \in V$，在第3行中计算 $\operatorname{Pr}\left(u_{k} \mid \Phi\left(v_{j}\right)\right)$ 是不可行的。计算配分函数（归一化因子）成本昂贵。如果我们将顶点分配给二进制树的叶子，预测问题就会变成树中特定路径的概率最大化(见 Figure 3c)。如果到顶点 $u_k$ 的路径是由一系列树节点识别的$\left(b_{0}, b_{1}, \ldots, b_{\lceil\log |V|\rceil}\right)$，$(b_0=root，b_{\lceil\log |V|\rceil}=u_{k})$，那么

　　　　$\operatorname{Pr}\left(u_{k} \mid \Phi\left(v_{j}\right)\right)=\prod \limits _{l=1}^{\lceil\log |V|\rceil} \operatorname{Pr}\left(b_{l} \mid \Phi\left(v_{j}\right)\right)$

　　现在，$\operatorname{Pr}\left(b_{l} \mid \Phi\left(v_{j}\right)\right)$ 可以通过分配给节点 $b_l$ 的父节点的二进制分类器来建模。这降低了计算 $\operatorname{Pr}\left(u_{k} \mid \Phi\left(v_{j}\right)\right)$ 的计算复杂度，从 $O(|V|)$ 降低到 $O(log|V|)$ 。我们可以通过为随机行走中的频繁顶点分配更短的路径来进一步加快训练过程。霍夫曼编码用于减少树中频繁元素的访问时间。

8 Experiment

dataset

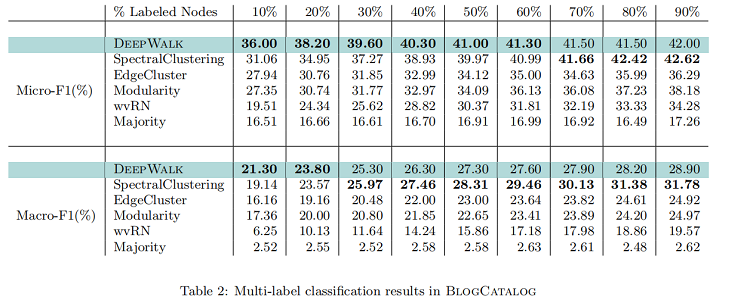
- $BlogCatalog$ 是博客作者的社交关系网络。标签代表作者提供的主题类别。
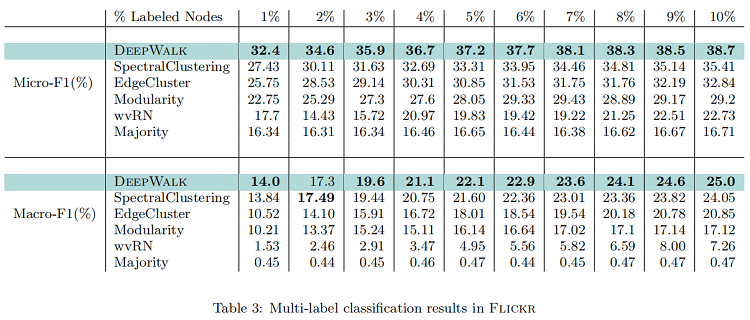
- $Flickr$ 是照片分享网站用户之间的联系网络。标签代表用户的兴趣组，如“黑白照片”。
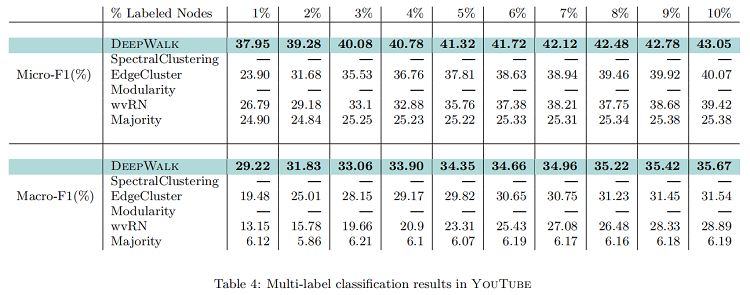
- $YouTube$ 是流行的视频分享网站用户之间的社交网络。这里的标签代表喜欢不同类型视频（例如动漫和摔跤）的观众群体。