哈达玛积

　　哈达玛积(Hadamard product)是矩阵的一类运算，若 $A=(a_{ij})$ 和 $B=(b_{ij})$ 是两个同阶矩阵，若,则称矩阵 $c_{ij}=a_{ij}\times b_{ij}$ 为 $A$ 和 $B$ 的哈达玛积，或称基本积。

1 定义

　　设  $A, B \in \mathbb{C}^{m \times n}$  且  $A=\left\{a_{i j}\right\}$，$B=\left[b_{i j}\right]$， 称  $m \times n$  矩阵

　　　　$\left[\begin{array}{cccc}a_{11} b_{11} & a_{12} b_{12} & \cdots & a_{1 n} b_{1 n} \\a_{21} b_{21} & a_{22} b_{22} & \cdots & a_{2 n} b_{2 n} \\\vdots & \vdots & & \vdots \\a_{m 1} b_{m 1} & a_{m 2} b_{m 2} & \cdots & a_{m n} b_{m n}\end{array}\right]$

　　为矩阵 $A$ 与 $B$ 的哈达玛(Hadamard)积，记作  $A \circ B$ 。

　　　　　　

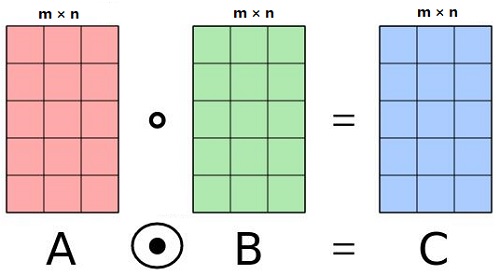
 　　　　$\left(\begin{array}{lll}\mathrm{a}_{11} & \mathrm{a}_{12} & \mathrm{a}_{13} \\\mathrm{a}_{21} & \mathrm{a}_{22} & \mathrm{a}_{23} \\\mathrm{a}_{31} & \mathrm{a}_{32} & \mathrm{a}_{33}\end{array}\right) \odot\left(\begin{array}{lll}\mathrm{b}_{11} & \mathrm{~b}_{12} & \mathrm{~b}_{13} \\\mathrm{~b}_{21} & \mathrm{~b}_{22} & \mathrm{~b}_{23} \\\mathrm{~b}_{31} & \mathrm{~b}_{32} & \mathrm{~b}_{33}\end{array}\right)=\left(\begin{array}{llllll}\mathrm{a}_{11} & \mathrm{~b}_{11} & \mathrm{a}_{12} & \mathrm{~b}_{12} & \mathrm{a}_{13} & \mathrm{~b}_{13} \\\mathrm{a}_{21} & \mathrm{~b}_{21} & \mathrm{a}_{22} & \mathrm{~b}_{22} & \mathrm{a}_{23} & \mathrm{~b}_{23} \\\mathrm{a}_{31} & \mathrm{~b}_{31} & \mathrm{a}_{32} & \mathrm{~b}_{32} & \mathrm{a}_{33} & \mathrm{~b}_{33}\end{array}\right)$

2 哈达玛积的主要性质

　　由矩阵的 Hadamard 积的定义显然有

　　　　$A \circ 0=0 \circ A=0, A \circ B=B \circ A,(A+B) \circ C=(A \circ C)+(B \circ C)$

　　并且
　　　　$A \circ B=P(A \otimes B) Q$
　　其中
　　　　$\begin{array}{l}P=E_{11}+E_{2, m+2}+\ldots+E_{m, m^{2}} \in \mathbb{R}^{m \times m^{2}} \\Q=E_{11}+E_{n+2,2}+\ldots+E_{n^{2} \times n} \in \mathbb{R}^{n^{2} \times n}\end{array}$
　　特别地，若 $m=n$ ，则 $Q=P^{T}$ ，且

　　　　$A \circ B=P(A \otimes B) P^{T}$
　　因而 $A \circ B$ 是 $A \otimes B$ 的主子阵，故有下面的命题。
　　命题1 设 $A, B \in \mathbb{C}^{m \times n}$, $\operatorname{rankA}=r_{1}, \operatorname{rank} B=r_{2}$ , 则
　　　　$\operatorname{rank}(A \circ B) \leqslant r_{1} r_{2}$
　　命题2 设 $A, B \in \mathbb{C}^{m \times n}$，$A, B \geq 0$, 则
　　　　$\lambda_{\min }(A \circ B) \geqslant \lambda_{\min }(A) \lambda_{\min }(B)$
　　命题3 设 $A, B \in \mathbb{C}^{m \times n}$, 若 $A >0, B>0$ , 则 $A \circ B>0$。
　　命题4 设 $A, B \in \mathbb{C}^{m \times n}$ ,
　　　　$D=\operatorname{diag}\left(d_{1}, d_{2}, \ldots, d_{n}\right), E=\operatorname{diag}\left(e_{1}, \ldots, e_{n}\right)$
　　则
　　　　$(D A) \circ(B E)=A \circ(D B E)=(D A E) \circ B$