论文解读(GAT)《Graph Attention Networks》
论文信息
论文标题:Graph Attention Networks
论文作者:Petar Velickovic、Guillem Cucurull、Arantxa Casanova、Adriana Romero、P. Lio’、Yoshua Bengio
论文来源:2018 ICLR
论文地址:download
论文代码:download
1 Introduction
GCN 消息传递机制版本:
$h_{i}^{(l+1)}=\sigma\left(b^{(l)}+\sum\limits_{j \in \mathcal{N}(i)} \frac{1}{c_{j i}} h_{j}^{(l)} W^{(l)}\right)$
$c_{j i}=\sqrt{|\mathcal{N}(j)|} \sqrt{|\mathcal{N}(i)|}$
GCN 矩阵版本:
$H=\hat{A}X W$
$\hat{A}=\tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}}$
GAT 消息传递机制版本:
$h_{i}^{(l+1)}=\sum\limits _{j \in \mathcal{N}(i)} \alpha_{i, j} W^{(l)} h_{j}^{(l)}$
$\alpha_{i j}^{l} =\operatorname{softmax}_{\mathrm{i}}\left(e_{i j}^{l}\right) $
$e_{i j}^{l} =\operatorname{LeakyReLU}\left(\vec{a}^{T}\left[W h_{i} \| W h_{j}\right]\right)$
对于 GCN 和 GAT 我个人的理解:GCN 的 “注意力系数” $\frac{1}{c_{j i}}$ 是固定的,而 GAT 的注意力系数 $\alpha_{i, j}$ 是自适应的【相当于执行了 一层 MLP,这是由于 $\vec{a}$ 是一个可学习参数】。
Attention 机制的特性:
- 操作效率高,在跨节点对中可并行计算;
- 通过对相邻节点指定任意权值,可应用于不同度的图节点;
- 该模型直接适用于归纳学习问题,包括讲模型推广到完全不可见图的任务;
2 GAT Method
GAT 有两种思路:
-
- Global graph attention:即每一个顶点 $i$ 对图中任意顶点 $j$ 进行注意力计算。优点:可以很好的完成 inductive 任务,因为不依赖于图结构。缺点:数据本身图结构信息丢失,容易造成很差的结果;
- Mask graph attention:注意力机制的运算只在邻居顶点上进行,即本文的做法;
具体代码实现只需要注释下面 Mask graph attention 核心代码第三行:
e = self.leakyrelu(torch.matmul(a_input, self.a).squeeze(2)) #e.shape = [2708, 2708]
zero_vec = -9e15 * torch.ones_like(e)
attention = torch.where(adj > 0, e, zero_vec) # 将邻接矩阵中小于0的变成负无穷
attention = F.softmax(attention, dim=1) # 按行求softmax。 sum(axis=1) === 1
单层 GAT layer 的输入:
$\mathbf{h}=\left\{\vec{h}_{1}, \vec{h}_{2}, \ldots, \vec{h}_{N}\right\}, \vec{h}_{i} \in \mathbb{R}^{F}$
其中:
-
- $N$ 表示节点集中节点个数;
- $F$ 表示相应的特征向量维度;
单层 GAT layer 的输出:
$\mathbf{h}^{\prime}=\left\{\vec{h}_{1}^{\prime}, \vec{h}_{2}^{\prime}, \ldots, \vec{h}_{N}^{\prime}\right\}, \vec{h}_{i}^{\prime} \in \mathbb{R}^{F^{\prime}}$
其中,$F^{\prime}$ 表示节点输出特征向量维度。
一层 GAT layer 的结构如下图所示:
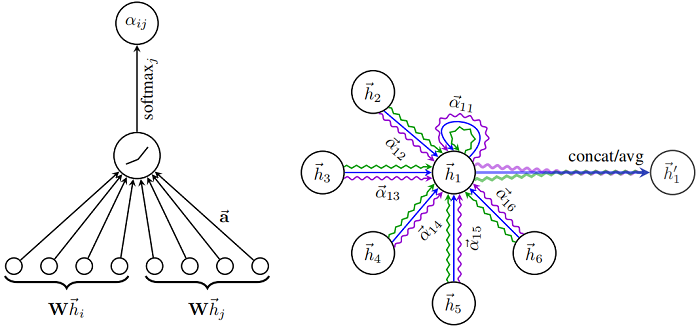
Step1:做 self-attention 处理 :
$e_{i j}=a\left(\mathbf{W} \vec{h}_{i}, \mathbf{W} \vec{h}_{j}\right)$
$e_{ij}$ 表明节点 $j$ 和节点 $i$ 之间的重要性, $e \in\mathbb{R}^{N \times N} $,此时重要性并没有归一化。
其中, $a$ 是一个 $\mathbb{R}^{F^{\prime}} \times \mathbb{R}^{F^{\prime}} \rightarrow \mathbb{R}$ 的映射,$W \in \mathbb{R}^{F^{\prime} \times F}$ 是一个权重矩阵(被所有 $\vec{h}_{i}$ 的共享)。
Step2:将节点之间的重要性归一化(以节点 $i$ 和 节点 $j$ 为例):
$\alpha_{i j}=\operatorname{softmax}_{j}\left(e_{i j}\right)={\large \frac{\exp \left(e_{i j}\right)}{\sum \limits _{k \in \mathcal{N}_{i}} \exp \left(e_{i k}\right)}} $
图注意力机制的完全形式为:
$\alpha_{i j}=\frac{\exp \left(\operatorname{LeakyReLU}\left(\overrightarrow{\mathbf{a}}^{T}\left[\mathbf{W} \vec{h}_{i} \| \mathbf{W} \vec{h}_{j}\right]\right)\right)}{\sum \limits _{k \in \mathcal{N}_{i}} \exp \left(\operatorname{LeakyReLU}\left(\overrightarrow{\mathbf{a}}^{T}\left[\mathbf{W} \vec{h}_{i} \| \mathbf{W} \vec{h}_{k}\right]\right)\right)}$
Step3:计算节点表示:
$\vec{h}_{i}^{\prime}=\sigma\left(\sum \limits _{j \in \mathcal{N}_{\mathbf{i}}} \alpha_{i j} \mathbf{W} \vec{h}_{j}\right)$
Step4:为提高模型拟合能力,本文采用了多头注意力机制,即使用多个 $W^{k}$ 计算 self-attention,然后将各 $W^{k}$ 计算得到的结果合并(拼接或求和):
$\vec{h}_{i}^{\prime}=\sigma\left(\frac{1}{K} \sum \limits _{k=1}^{K} \sum \limits_{j \in \mathcal{N}_{i}} \alpha_{i j}^{k} \mathbf{W}^{k} \vec{h}_{j}\right)$
此时 $\vec{h}_{i}^{\prime} \in \mathbb{R}^{ F^{\prime}}$。
论文模型架构:【采用的是拼接】
GAT(
(attention_0): GraphAttentionLayer (1433 -> 8)
(attention_1): GraphAttentionLayer (1433 -> 8)
(attention_2): GraphAttentionLayer (1433 -> 8)
(attention_3): GraphAttentionLayer (1433 -> 8)
(attention_4): GraphAttentionLayer (1433 -> 8)
(attention_5): GraphAttentionLayer (1433 -> 8)
(attention_6): GraphAttentionLayer (1433 -> 8)
(attention_7): GraphAttentionLayer (1433 -> 8)
(out_att): GraphAttentionLayer (64 -> 7)
)
3 Example
举例:
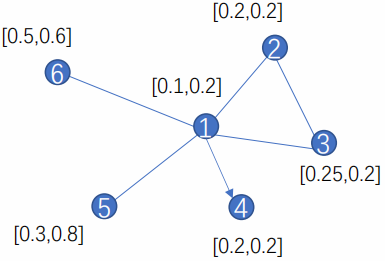
假设:$\alpha=[1,1,1,1] \quad w=[[1,0],[0,1]]$
那么:
$\begin{array}{l}e_{12}=\alpha \cdot[0.1,0.2,0.2,0.2]=0.7 \\e_{13}=\alpha \cdot[0.1,0.2,0.25,0.2]=0.75 \\e_{14}=0 \\e_{15}=\alpha \cdot[0.1,0.2,0.3,0.8]=1.4 \\e_{16}=\alpha \cdot[0.1,0.2,0.5,0.6]=1.4\end{array}$
根据
$ e_{i j}=a\left(\mathbf{W} \vec{h}_{i}, \mathbf{W} \vec{h}_{j}\right)$
$\alpha_{i j}={\large \frac{\exp \left(\operatorname{LeakyReLU}\left(\overrightarrow{\mathbf{a}}^{T}\left[\mathbf{W} \vec{h}_{i} \| \mathbf{W} \vec{h}_{j}\right]\right)\right)}{\sum_{k \in \mathcal{N}_{i}} \exp \left(\operatorname{LeakyReLU}\left(\overrightarrow{\mathbf{a}}^{T}\left[\mathbf{W} \vec{h}_{i} \| \mathbf{W} \vec{h}_{k}\right]\right)\right)}} $
计算节点 $1$ 和节点 $2$ 之间的重要性:
$\alpha_{12}={\large \frac{\exp \left(\operatorname{LeakReLU}\left(e_{12}\right)\right)}{\exp \left(\operatorname{LeakReLU}\left(e_{12}\right)\right)+\cdots+\exp \left(\operatorname{LeakReLU}\left(e_{16}\right)\right)}} $
根据 $\vec{h}_{i}^{\prime}=\sigma\left(\sum_{j \in \mathcal{N}_{i}} \alpha_{i j} \mathbf{W} \vec{h}_{j}\right)$ 计算节点 $1$ 的表示:
$\vec{h}_{1}^{\prime}=\sigma\left(\alpha_{12} \cdot W \cdot \vec{h}_{2}+\alpha_{13} \cdot W \cdot \vec{h}_{3} \ldots .\right)=\sigma\left(\alpha_{12} \cdot W \cdot[0.2,0.2]+\ldots .\right)$
4 Experiment
Dataset
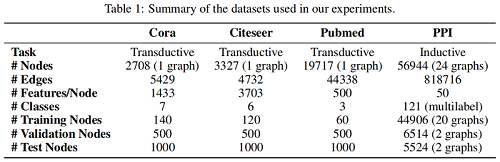
Transductive learning
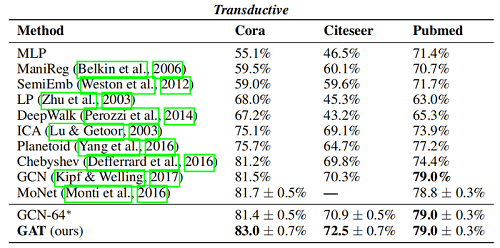
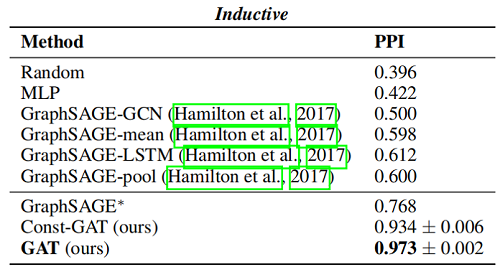
Inductive learning

class GAT(nn.Module):
def __init__(self, nfeat, nhid, nclass, dropout, alpha, nheads):
"""Dense version of GAT."""
super(GAT, self).__init__()
self.dropout = dropout
self.attentions = [GraphAttentionLayer(nfeat, nhid, dropout=dropout, alpha=alpha, concat=True) for _ in range(nheads)]
for i, attention in enumerate(self.attentions):
self.add_module('attention_{}'.format(i), attention)
self.out_att = GraphAttentionLayer(nhid * nheads, nclass, dropout=dropout, alpha=alpha, concat=False) # 第二层(最后一层)的attention layer
def forward(self, x, adj):
x = F.dropout(x, self.dropout, training=self.training)
x = torch.cat([att(x, adj) for att in self.attentions], dim=1) # 将每层attention拼接
x = F.dropout(x, self.dropout, training=self.training)
x = F.elu(self.out_att(x, adj)) # 第二层的attention layer
return F.log_softmax(x, dim=1)
Layer:

class GraphAttentionLayer(nn.Module):
def __init__(self, in_features, out_features, dropout, alpha, concat=True):
super(GraphAttentionLayer, self).__init__()
self.dropout = dropout
self.in_features = in_features
self.out_features = out_features
self.alpha = alpha
self.concat = concat
self.W = nn.Parameter(torch.empty(size=(in_features, out_features)))
nn.init.xavier_uniform_(self.W.data, gain=1.414)
self.a = nn.Parameter(torch.empty(size=(2 * out_features, 1))) # concat(V,NeigV)
nn.init.xavier_uniform_(self.a.data, gain=1.414)
self.leakyrelu = nn.LeakyReLU(self.alpha)
def forward(self, h, adj):
Wh = torch.mm(h, self.W) # h.shape: (N, in_features), Wh.shape: (N, out_features)
a_input = self._prepare_attentional_mechanism_input(Wh) # a_input.shape = torch.Size([2708, 2708, 16])=(N,N,2 * out_features)
e = self.leakyrelu(torch.matmul(a_input, self.a).squeeze(2)) #e.shape = torch.Size([2708, 2708])
# 之前计算的是一个节点和所有节点的attention,其实需要的是连接的节点的attention系数
zero_vec = -9e15 * torch.ones_like(e)
attention = torch.where(adj > 0, e, zero_vec) # 将邻接矩阵中小于0的变成负无穷
attention = F.softmax(attention, dim=1) # 按行求softmax。 sum(axis=1) === 1
attention = F.dropout(attention, self.dropout, training=self.training)
h_prime = torch.matmul(attention, Wh) # 聚合邻居函数
if self.concat:
return F.elu(h_prime) # elu-激活函数
else:
return h_prime
def _prepare_attentional_mechanism_input(self, Wh):
N = Wh.shape[0] # number of nodes
#Wh.shape: (N, out_features)
Wh_repeated_in_chunks = Wh.repeat_interleave(N, dim=0) #每个节点顺序复制N遍节点表示
Wh_repeated_alternating = Wh.repeat(N, 1)
# Wh_repeated_in_chunks.shape == Wh_repeated_alternating.shape == (N * N, out_features)
all_combinations_matrix = torch.cat([Wh_repeated_in_chunks, Wh_repeated_alternating], dim=1)
# all_combinations_matrix.shape == (N * N, 2 * out_features)
return all_combinations_matrix.view(N, N, 2 * self.out_features)
def __repr__(self):
return self.__class__.__name__ + ' (' + str(self.in_features) + ' -> ' + str(self.out_features) + ')'
因上求缘,果上努力~~~~ 作者:别关注我了,私信我吧,转载请注明原文链接:https://www.cnblogs.com/BlairGrowing/p/15339757.html



 浙公网安备 33010602011771号
浙公网安备 33010602011771号