Self-attention(自注意力机制)
self-attention是什么?
一个 self-attention 模块接收 n 个输入,然后返回 n 个输出。自注意力机制让每个输入都会彼此交互(自),然后找到它们应该更加关注的输入(注意力)。自注意力模块的输出是这些交互的聚合和注意力分数。
self-attention模块包括以下步骤:
- 准备输入
- 初始化权重
- 推导key, query 和 value
- 计算输入1 的注意力得分
- 计算 softmax
- 将分数与值相乘
- 将权重值相加,得到输出 1
- 对输入 2 和输入 3 重复步骤 4-7
第一步:准备输入
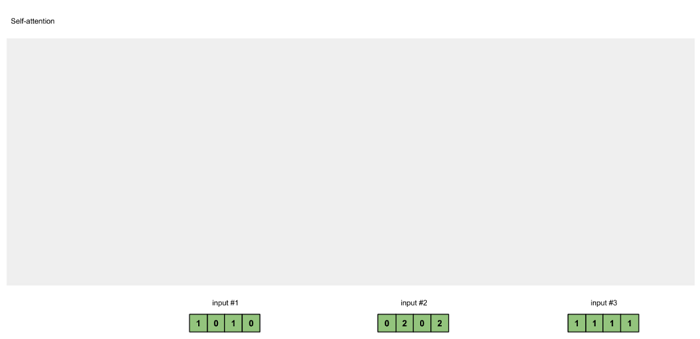
图1.1: 准备输入
假设有 3 个输入,每个输入的维度为 4.
Input 1: [1, 0, 1, 0]
Input 2: [0, 2, 0, 2]
Input 3: [1, 1, 1, 1]
第二步:初始化权重
每个输入必须有 3 个表征,分别被称为键(key,橙色)、查询(query,红色)和值(value,紫色)。在此示例中,我们设这些表征的维度为 3。因为每个输入的维度为 4,所以这意味着每组权重的形状为 4×3。

图1.2:从每个输入得出键、查询和值的表示
为了得到这些表征,每个输入(绿色)都要与一组键的权重、一组查询的权重、一组值的权重相乘。在这个示例中,我们按如下方式初始化这三个权重:
键的权重:
[[0, 0, 1],
[1, 1, 0],
[0, 1, 0],
[1, 1, 0]]
查询的权重:
[[1, 0, 1],
[1, 0, 0],
[0, 0, 1],
[0, 1, 1]]
值的权重:
[[0, 2, 0],
[0, 3, 0],
[1, 0, 3],
[1, 1, 0]]
备注:在神经网络设置中,这些权重通常是较小的数值,初始化也是使用合适的随机分布来实现,比如高斯分布、Xavier 分布、Kaiming 分布。
第三步:推导键、查询和值
现在我们有三组权重了,我们来实际求取每个输入的键、查询和值的表征:
输入 1 的键表征:
[0, 0, 1]
[1, 0, 1, 0] x [1, 1, 0] = [0, 1, 1]
[0, 1, 0]
[1, 1, 0]
使用同样一组权重求取输入 2 的键表征:
[0, 0, 1]
[0, 2, 0, 2] x [1, 1, 0] = [4, 4, 0]
[0, 1, 0]
[1, 1, 0]
使用同样一组权重求取输入 3 的键表征:
[0, 0, 1]
[1, 1, 1, 1] x [1, 1, 0] = [2, 3, 1]
[0, 1, 0]
[1, 1, 0]
向量化以上运算能实现更快的速度:
[0, 0, 1]
[1, 0, 1, 0] [1, 1, 0] [0, 1, 1]
[0, 2, 0, 2] x [0, 1, 0] = [4, 4, 0]
[1, 1, 1, 1] [1, 1, 0] [2, 3, 1]
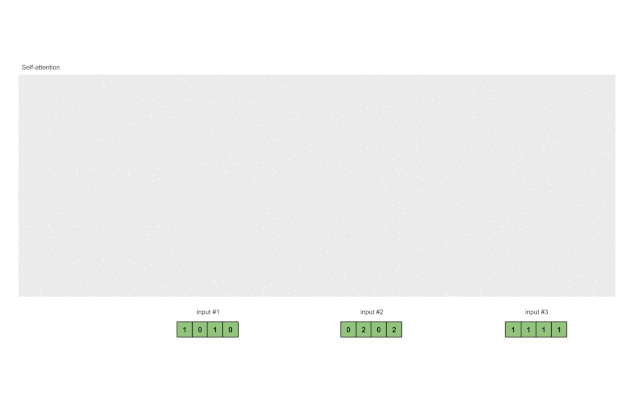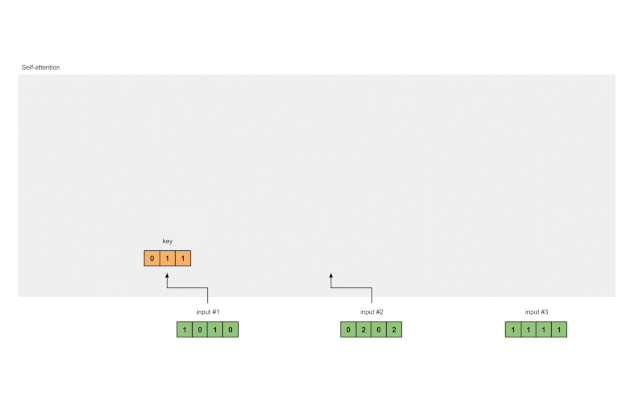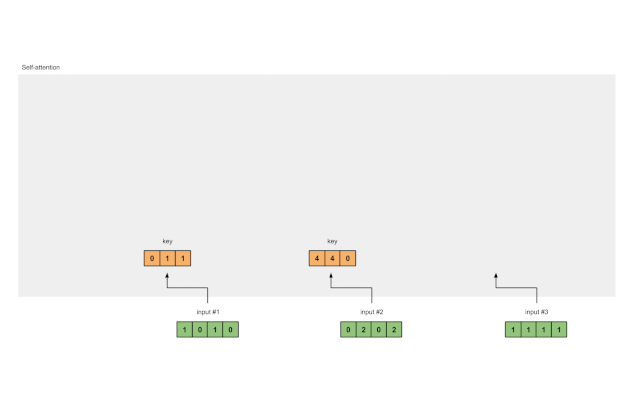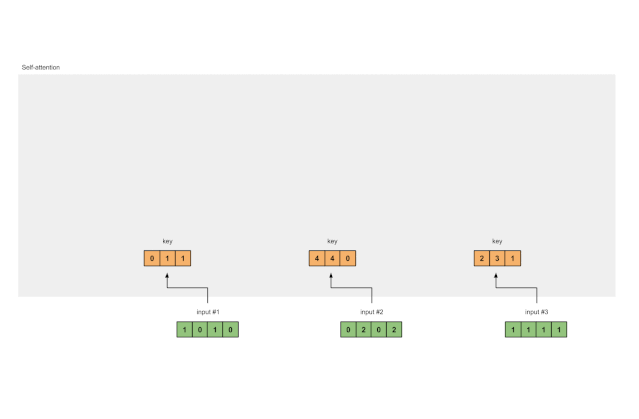
图1.3a:从每个输入推导出键表示
通过类似的方式,我们求取每个输入的值表征:
[0, 2, 0]
[1, 0, 1, 0] [0, 3, 0] [1, 2, 3]
[0, 2, 0, 2] x [1, 0, 3] = [2, 8, 0]
[1, 1, 1, 1] [1, 1, 0] [2, 6, 3]
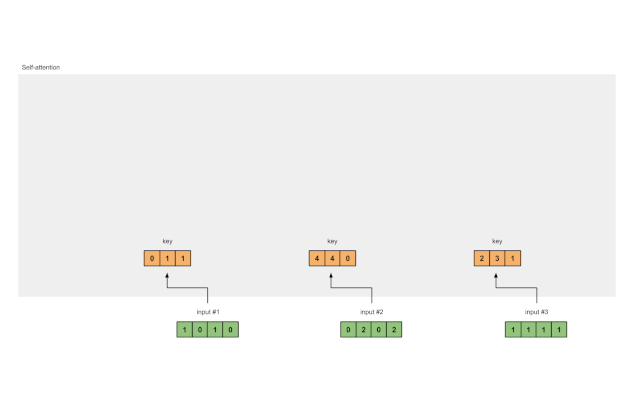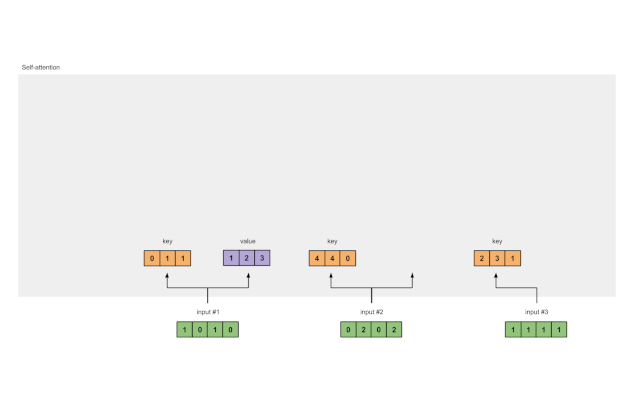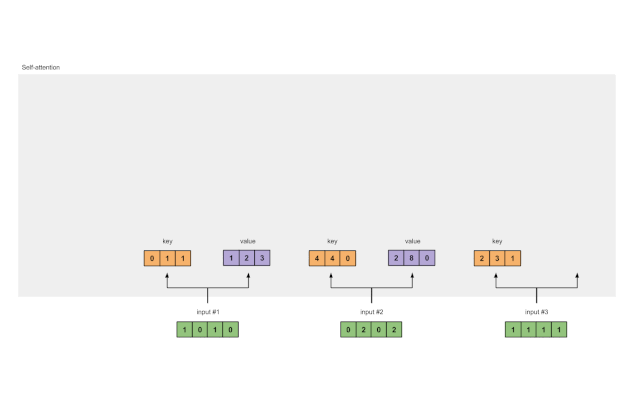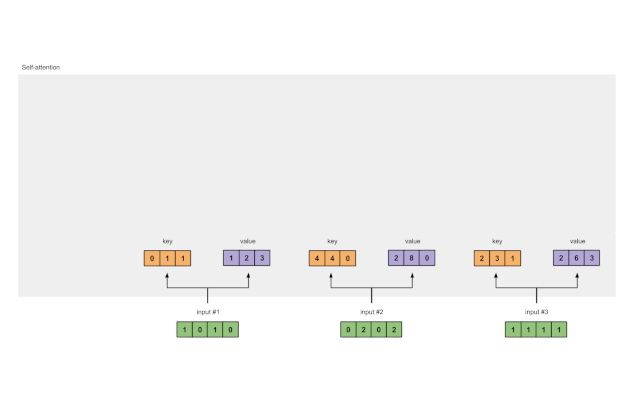
图1.3b:从每个输入推导出值表示
最后还有查询表征:
[1, 0, 1]
[1, 0, 1, 0] [1, 0, 0] [1, 0, 2]
[0, 2, 0, 2] x [0, 0, 1] = [2, 2, 2]
[1, 1, 1, 1] [0, 1, 1] [2, 1, 3]
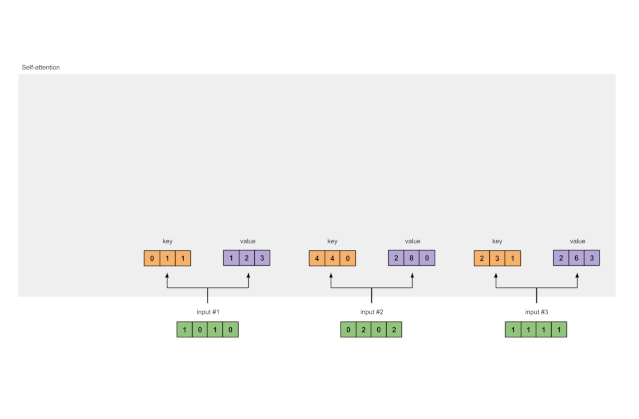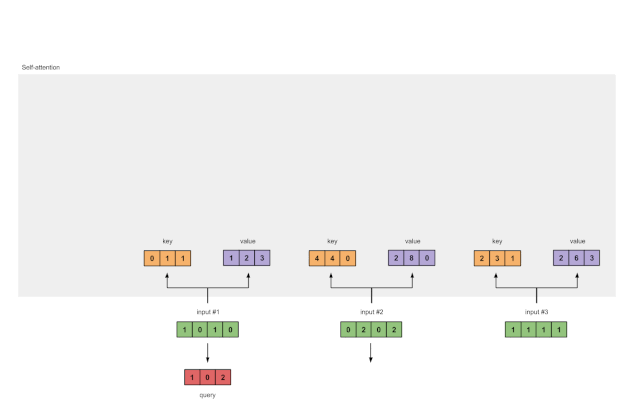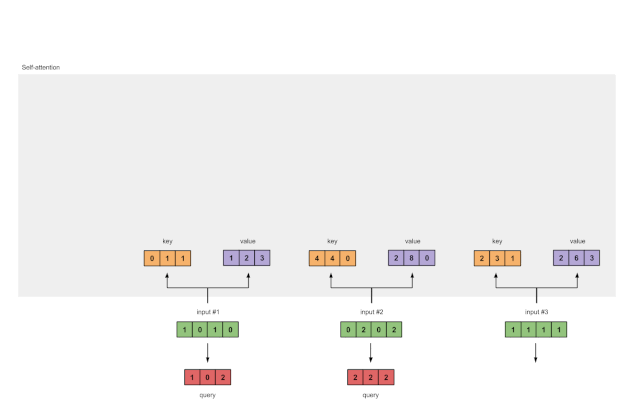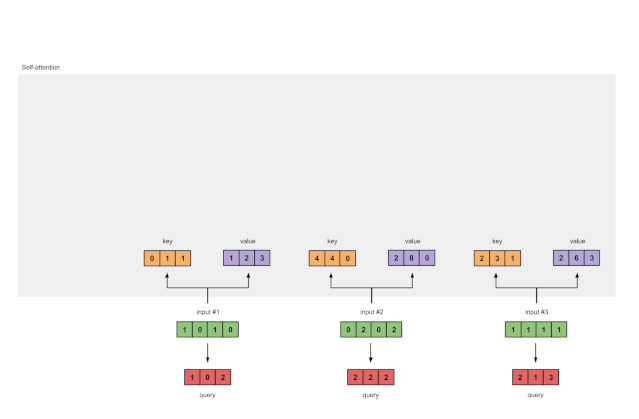
图1.3b:从每个输入推导出查询表示
第四步:计算输入1 的 attention scores
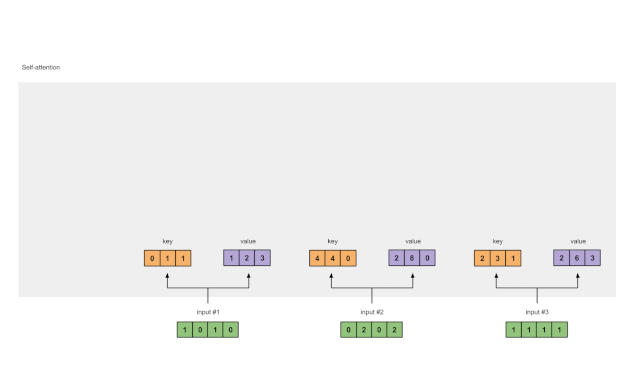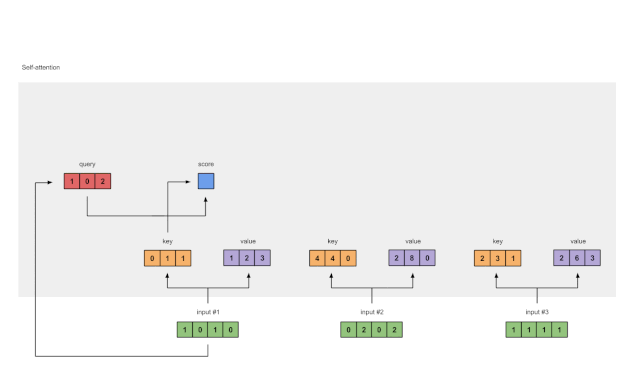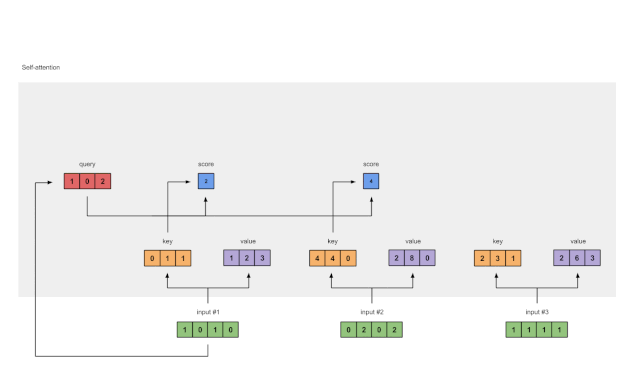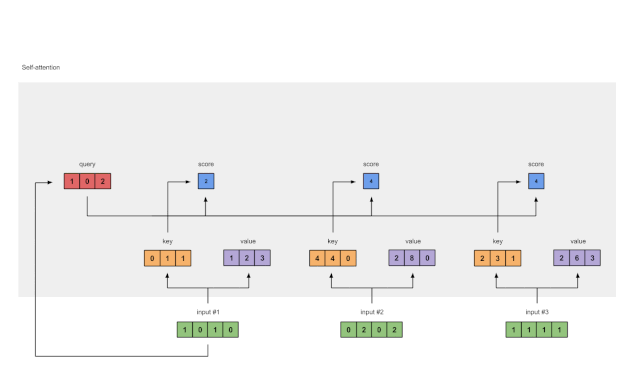
图1.4:从查询1中计算注意力得分(蓝色)
为了获得注意力得分,我们首先在输入1的查询(红色)和所有键(橙色)之间取一个点积。因为有3个键表示(因为有3个输入),我们得到3个注意力得分(蓝色)。
[0, 4, 2]
[1, 0, 2] x [1, 4, 3] = [2, 4, 4]
[1, 0, 1]
注意这里仅使用了输入 1 的查询。后面我们会为其它查询重复同一步骤。
备注:上面的运算也被称为点积注意力(dot product attention),这是众多评分函数中的一个,其它评分函数还包括扩展式点积和 additive/concat
第五步:计算 softmax
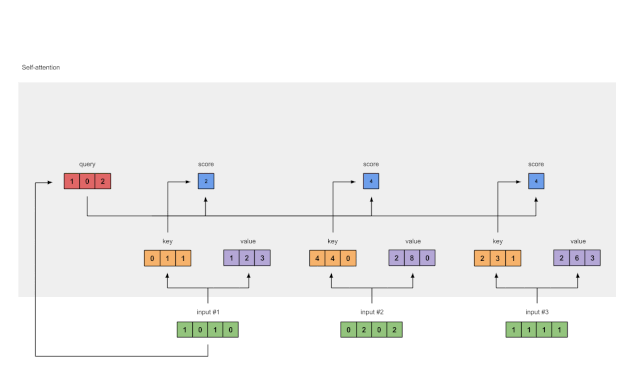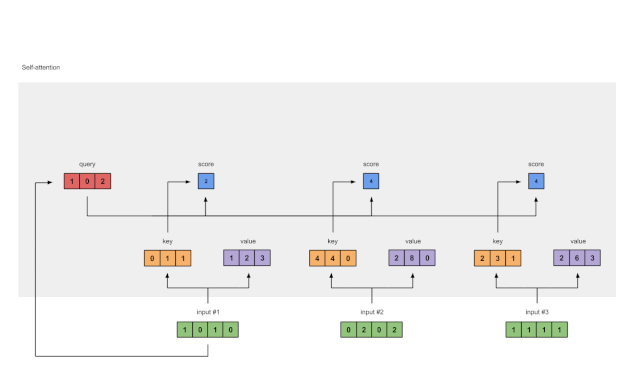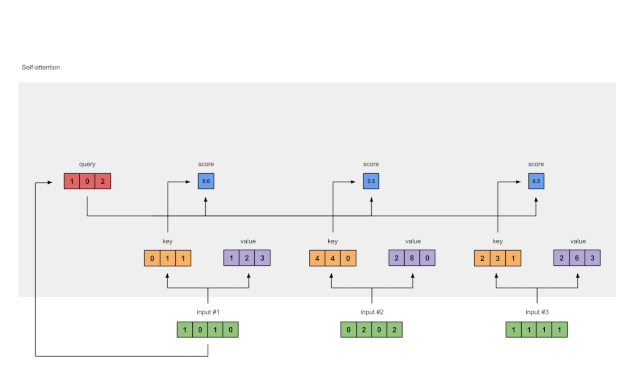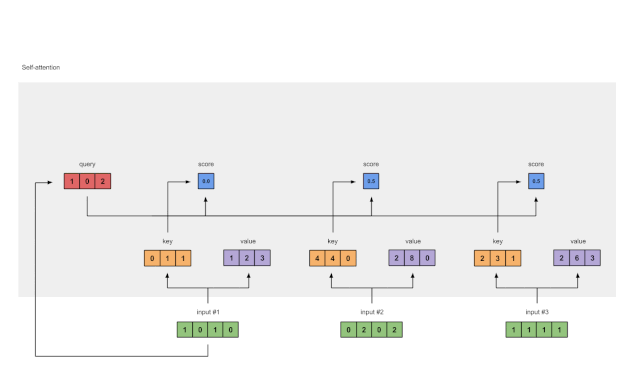
图1.5:Softmax注意力评分(蓝色)
在所有注意力得分中使用softmax(蓝色)。
softmax([2, 4, 4]) = [0.0, 0.5, 0.5]
第六步:将分数与值相乘
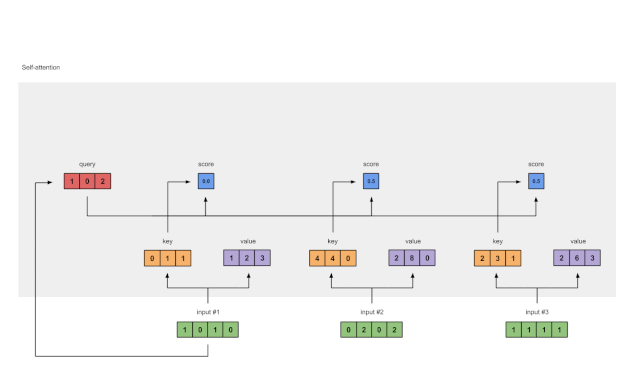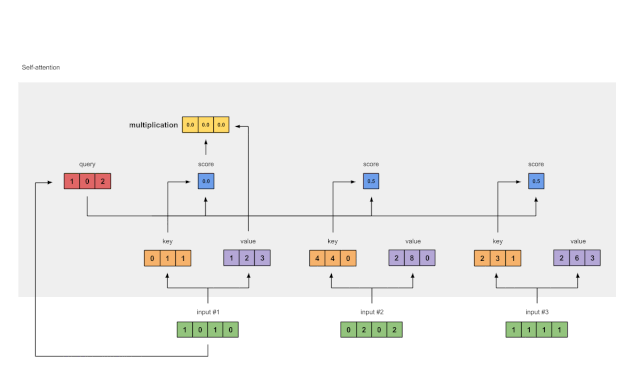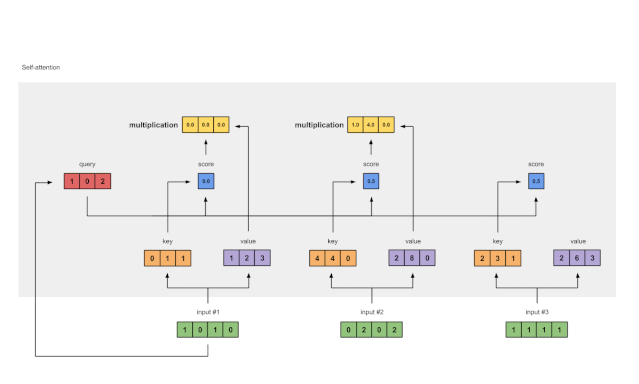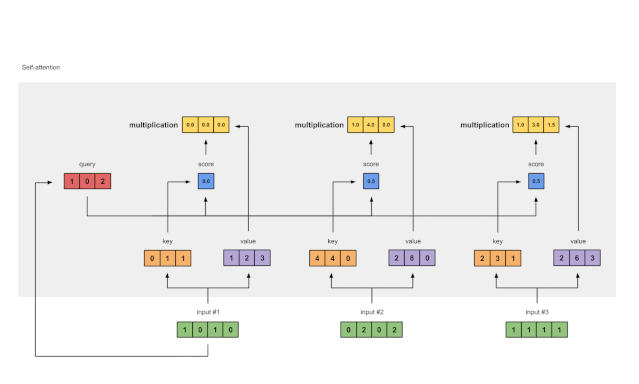
图1.6:由值(紫色)和分数(蓝色)的相乘推导出加权值表示(黄色)
每个输入的softmaxed attention 分数(蓝色)乘以相应的值(紫色)。结果得到3个对齐向量(黄色)。在本教程中,我们将它们称为加权值。
1: 0.0 * [1, 2, 3] = [0.0, 0.0, 0.0]
2: 0.5 * [2, 8, 0] = [1.0, 4.0, 0.0]
3: 0.5 * [2, 6, 3] = [1.0, 3.0, 1.5]
第七步:将加权值相加得到输出1
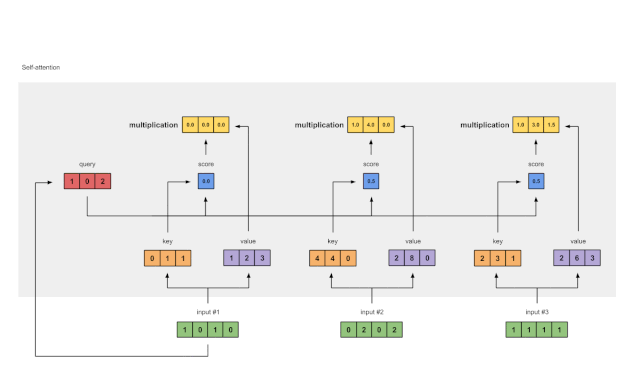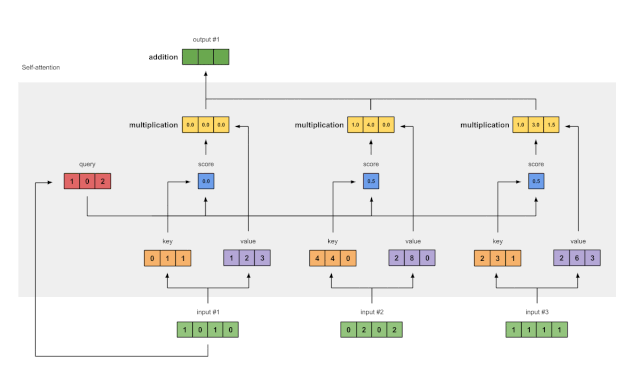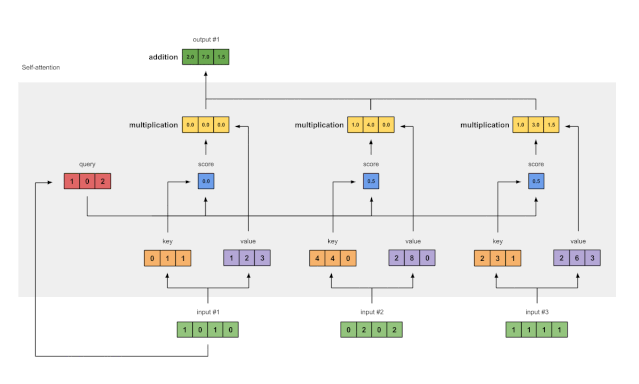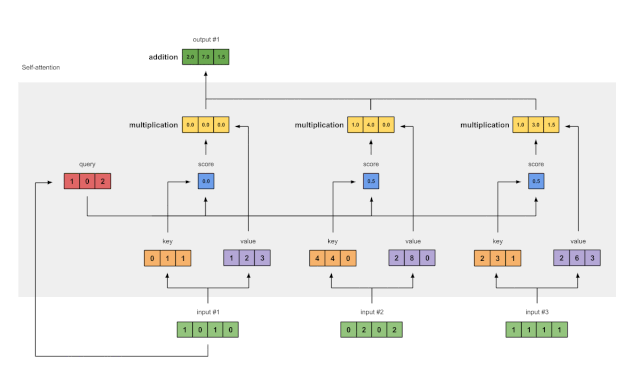
图1.7:将所有加权值(黄色)相加,得到输出1(深绿色)
将所有加权值(黄色)按元素指向求和:
[0.0, 0.0, 0.0]
+ [1.0, 4.0, 0.0]
+ [1.0, 3.0, 1.5]
-----------------
= [2.0, 7.0, 1.5]
所得到的向量 [2.0, 7.0, 1.5](深绿色)是输出 1,这是基于输入 1 的查询表征与所有其它键(包括其自身的)的交互而得到的。
第八步:为输入 2 和 3 重复 4-7 步骤
现在已经完成了对输出 1 的求解,我们再为输出 2 和输出 3 重复步骤 4-7。
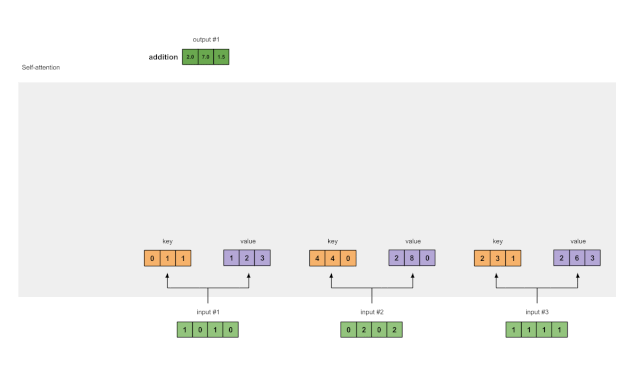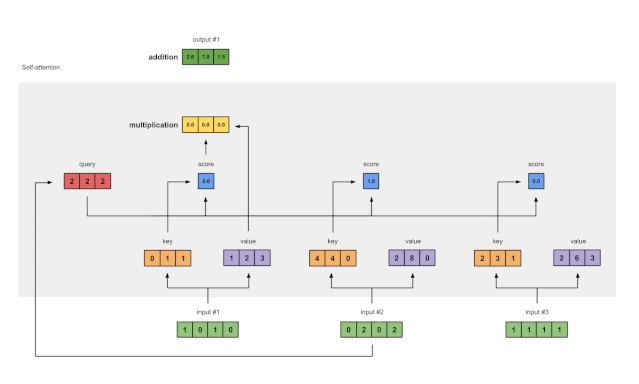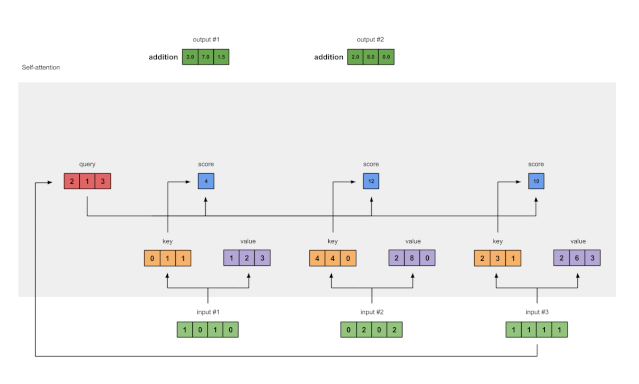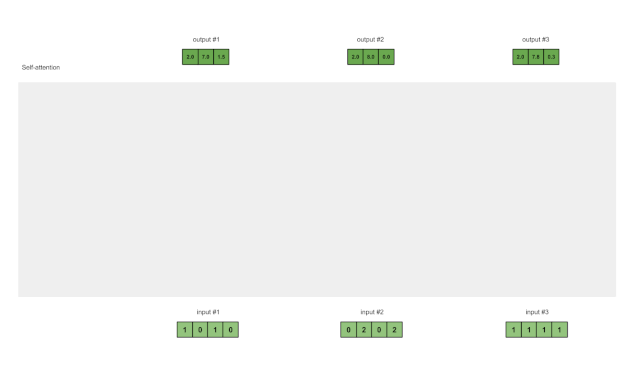
图1.8:对输入2和输入3重复前面的步骤
代码
步骤1:准备输入
import torch
x = [
[1, 0, 1, 0], # Input 1
[0, 2, 0, 2], # Input 2
[1, 1, 1, 1] # Input 3
]
x = torch.tensor(x, dtype=torch.float32)
步骤2:初始化权重
w_key = [
[0, 0, 1],
[1, 1, 0],
[0, 1, 0],
[1, 1, 0]
]
w_query = [
[1, 0, 1],
[1, 0, 0],
[0, 0, 1],
[0, 1, 1]
]
w_value = [
[0, 2, 0],
[0, 3, 0],
[1, 0, 3],
[1, 1, 0]
]
w_key = torch.tensor(w_key, dtype=torch.float32)
w_query = torch.tensor(w_query, dtype=torch.float32)
w_value = torch.tensor(w_value, dtype=torch.float32)
步骤3: 推导键、查询和值
keys = x @ w_key
querys = x @ w_query
values = x @ w_value
print(keys)
# tensor([[0., 1., 1.],
# [4., 4., 0.],
# [2., 3., 1.]])
print(querys)
# tensor([[1., 0., 2.],
# [2., 2., 2.],
# [2., 1., 3.]])
print(values)
# tensor([[1., 2., 3.],
# [2., 8., 0.],
# [2., 6., 3.]])
步骤4:计算注意力得分
attn_scores = querys @ keys.T
# tensor([[ 2., 4., 4.], # attention scores from Query 1
# [ 4., 16., 12.], # attention scores from Query 2
# [ 4., 12., 10.]]) # attention scores from Query 3
步骤5:计算softmax
from torch.nn.functional import softmax
attn_scores_softmax = softmax(attn_scores, dim=-1)
# tensor([[6.3379e-02, 4.6831e-01, 4.6831e-01],
# [6.0337e-06, 9.8201e-01, 1.7986e-02],
# [2.9539e-04, 8.8054e-01, 1.1917e-01]])
# For readability, approximate the above as follows
attn_scores_softmax = [
[0.0, 0.5, 0.5],
[0.0, 1.0, 0.0],
[0.0, 0.9, 0.1]
]
attn_scores_softmax = torch.tensor(attn_scores_softmax)
步骤6:将得分和值相乘
weighted_values = values[:,None] * attn_scores_softmax.T[:,:,None]
# tensor([[[0.0000, 0.0000, 0.0000],
# [0.0000, 0.0000, 0.0000],
# [0.0000, 0.0000, 0.0000]],
#
# [[1.0000, 4.0000, 0.0000],
# [2.0000, 8.0000, 0.0000],
# [1.8000, 7.2000, 0.0000]],
#
# [[1.0000, 3.0000, 1.5000],
# [0.0000, 0.0000, 0.0000],
# [0.2000, 0.6000, 0.3000]]])
步骤7:求和加权值
outputs = weighted_values.sum(dim=0)
# tensor([[2.0000, 7.0000, 1.5000], # Output 1
# [2.0000, 8.0000, 0.0000], # Output 2
# [2.0000, 7.8000, 0.3000]]) # Output 3
因上求缘,果上努力~~~~ 作者:别关注我了,私信我吧,转载请注明原文链接:https://www.cnblogs.com/BlairGrowing/p/15338310.html

