图卷积神经网络（GCN）原理详解

一 GCN简介

 　　　　

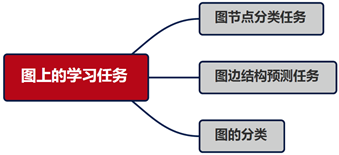
 　　GNN 模型主要研究图节点的表示（Graph Embedding），图边结构预测任务和图的分类问题，后两个任务也是基于 Graph Embedding 展开的。目前论文重点研究网络的可扩展性、动态性、加深网络。

　　

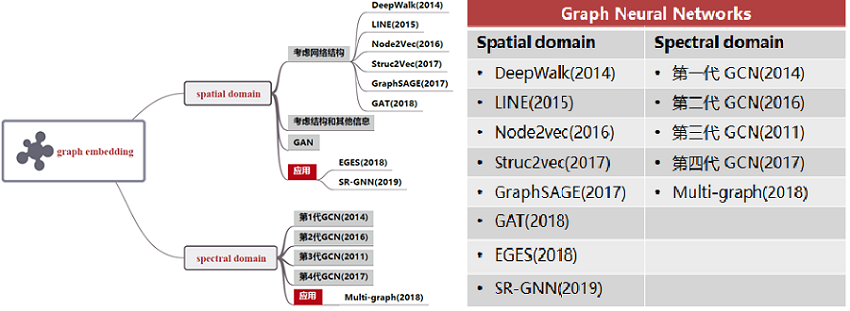
　　谱卷积有理论支持，但有时候会受到拉普拉斯算子的限制；而空间域卷积更加灵活，主要困难在于选择定量邻域上，没有统一理论。

　　未来方向：

• • 加深网络：研究表明随着网络层数增加，模型性能急剧下降。
  • 感受野：节点的感受野是指一组节点，包括中心节点和其近邻节点，有些节点可能只有一个近邻，而有些节点却有数千个近邻。
  • 可扩展性：大部分图神经网络并不能很好地扩展到大型图上。
  • 动态性和异质性：大多数当前的图神经网络都处理静态同质图。一方面，假设图架构是固定的。另一方面，假设图的节点和边来自同一个来源。

　　GCN模型具备深度学习的三种性质：

• • 层级结构（特征一层一层抽取，一层比一层更抽象，更高级）。
  • 非线性变换 （增加模型的表达能力）。
  • 端对端训练（不需要再去定义任何规则，只需要给图的节点一个标记，让模型自己学习，融合特征信息和结构信息。）。

　　GCN的四个特征：

• • GCN 是对卷积神经网络在 graph domain 上的自然推广。
  • 它能同时对节点特征信息与结构信息进行端对端学习，是目前对图数据学习任务的最佳选择。
  • 图卷积适用性极广，适用于任意拓扑结构的节点与图。
  • 在节点分类与边预测等任务上，在公开数据集上效果要远远优于其他方法。

　　通过谱图卷积的局部一阶近似，来确定卷积网络结构，通过图结构数据中部分有标签的节点数据对卷积神经网络结构模型训练，使网络模型对其余无标签的数据进行进一步分类。

二 spectral  domain

离散卷积是什么，在CNN中发挥什么作用？

　　离散卷积本质：加权求和

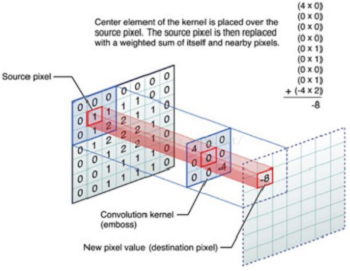
　　CNN 中的卷积本质上就是利用一个共享参数的过滤器（kernel），通过计算中心像素点以及相邻像素点的加权和来构成 feature map 实现空间特征的提取，当然加权系数就是卷积核的权重系数。

　　　　

GCN 中的 Graph 是指什么？为什么要研究GCN?

 　　CNN 有效地提取空间特征。需注意的是：CNN 处理的图像或者视频数据中像素点是排列成整齐的矩阵。这里对应了 Euclidean Structure 。

 　　　　

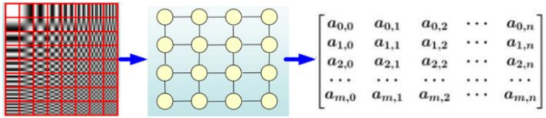
 　　与之相对应，科学研究中还有很多 Non Euclidean Structure 的数据。社交网络、信息网络中有很多类似的结构。

 　　　　

 　　实际上，这样的网络结构（Non Euclidean Structure）就是图论中抽象意义上的拓扑图。所以，Graph Convolutional Network 中的 Graph 是指图论中的用顶点和边建立相应关系的拓扑图。

为什么要研究 GCN ？

• 因为 CNN 无法处理非欧几里得结构的数据，学术上的表述是传统的离散卷积在非欧几里得结构的数据上无法保持平移不变性。通俗来说就是在拓扑图中每个顶点的相邻顶点数目都可能不同，那就没办法用一个同样尺寸的卷积核来进行卷积操作；
• 广义来讲任何数据在赋范空间内都可以建立拓扑关联，谱聚类就是应用了这样的思想，所以说拓扑连接是一种广义的数据结构，GCN有很大的应用空间。

三 提供拓扑图空间特征的两种方式

（1）vertex domain（spatial domain）

　　提取拓扑图上的空间特征，就是把每个顶点的相邻 neighbors 找出来

• 按照什么条件去找中心 vertex 的 neighbors，如何确定 receptive filed？ 　　
• 确定了 receptive field 之后，按照什么方式处理包含不同数目 neighbors 的特征？

　　　

　　这种方法主要的缺点如下：

• 每个顶点提取出来的 neighbors 不同，使得计算处理必须针对每个顶点。
• 提取特征的效果可能没有卷积好。

（2）spectral domain

　　借助图谱的理论来实现拓扑图上的卷积操作。

• 什么是Spectral graph theory？
  • 借助于图的拉普拉斯矩阵的特征值和特征向量来研究图的性质。

四 什么是拉普拉斯矩阵？为什么GCN要用拉普拉斯矩阵？

　　Graph Fourier Transformation及Graph Convolution定义都用到图的拉普拉斯矩阵，那么首先来介绍一下拉普拉斯矩阵。

　　对于图 $G=(V,E)$ 其 Laplacian 矩阵的定义为 $L=D−A$，其中 L 是 Laplacian 矩阵，D 是顶点的度矩阵，对角线上元素依次为各个顶点的度，A是图的邻接矩阵。

　　　　

　　常用的拉普拉斯矩阵实际用三种：

• • Combinatorial Laplacian：$L=D-A $
  • Symmetric normalized Laplacian： $L^{s y s}=D^{-1 / 2} L D^{-1 / 2} $
  • Random walk normalized Laplacian： $L^{r w}=D^{-1} L $

　　为什么GCN要用拉普拉斯矩阵？

• 拉普拉斯矩阵是对称矩阵，可以进行特征分解（谱分解）。
• 拉普拉斯矩阵只在中心顶点和一阶相连的顶点上有非 0 元素，其余之处均为 0。
• 通过拉普拉斯算子与拉普拉斯矩阵进类比。

 

 

 

 

参考

 

GCN总结