Random Walk

随机游走

几何布朗运动

　　几何布朗运动(Brownian motion)

　　布朗运动是将看起来连成一片的液体，在高倍显微镜下看其实是由许许多多分子组成的。液体分子不停地做无规则的运动，不断地随机撞击悬浮微粒。当悬浮的微粒足够小的时候，由于受到的来自各个方向的液体分子的撞击作用是不平衡的。在某一瞬间，微粒在另一个方向受到的撞击作用超强的时候，致使微粒又向其它方向运动，这样，就引起了微粒的无规则的运动就是布朗运动。（布朗运动指的是分子迸出的微粒的随机运动，而不是分子的随机运动。）即布朗运动代表了一种随机涨落现象。

---

随机游走

　　英文：Random Walk

　　定义：随机游走，概念接近于布朗运动，是布朗运动的理想数学状态。

　　核心概念：任何无规则行走者所带的守恒量都各自对应着一个扩散运输定律。

　　随机游走算法的基本思想是：

• • 从一个或一系列顶点开始遍历一张图。在任意一个顶点，遍历者将以概率 $1-a$ 游走到这个顶点的邻居顶点，以概率 $a$ 随机跳跃到图中的任何一个顶点，称 $a$ 为跳转发生概率，每次游走后得出一个概率分布，该概率分布刻画了图中每一个顶点被访问到的概率。用这个概率分布作为下一次游走的输入并反复迭代这一过程。当满足一定前提条件时，这个概率分布会趋于收敛。收敛后，即可以得到一个平稳的概率分布。

---

一维的随机游走

　　一维的随机游走可定义如下：每过一个单位时间，游走者从数轴位置 $x$ 出发以固定概率随机向左或向右移动一个单位。不妨将 $n$ 时刻游走者的位置记为 $L_n$,则有
　　　　$L_{n}=x+X_{1}+\cdots+X_{n}$

　　其中 $X_1,X_2,…,X_n$ 为相互独立的随机变量，满足

　　　　$P\left(X_{i}=1\right)=p=1-P\left(X_{i}=-1\right)$

　　最经典的一维随机游走问题有赌徒输光问题和酒鬼失足问题。

1.  赌徒在赌场赌博，赢的概率是 $p$，输的概率 $1-p$，每次的赌注为1元，假设赌徒最开始时有赌金1元，赢了赌金加1元，输了赌金减1元。问赌徒输光的概率是多少？
2.  一个醉鬼行走在一头是悬崖的道路上，酒鬼从距离悬崖仅一步之遥的位置出发，向前一步或向后退一步的概率皆为1/2，问酒鬼失足掉入悬崖的概率是多少？

　　二维随机游走示例代码：

　　　　　　

　　

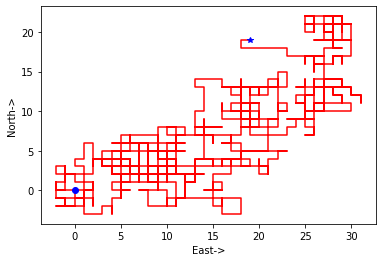
import random
import numpy as np
import matplotlib.pyplot as plt
N = 1000
d = 1 
x =np.zeros(N+1)
y =np.zeros(N+1)
x[0] = 0
y[0] = 0
for i in range(0,N,1):
    r = random.random()  #[0,1)
    if 0<=r<0.25 :
        y[i+1]=y[i]+d;x[i+1]=x[i]
    elif 0.25<=r<0.5:
        y[i+1]=y[i];x[i+1]=x[i]+d
    elif 0.5<=r<0.75:
        y[i+1]=y[i]-d;x[i+1]=x[i]
    else :
        y[i+1]=y[i]; x[i+1]=x[i]-d
plt.plot(x,y,'r',x[0],y[0],'bo',x[-1],y[-1],'b*')
plt.xlabel("East->")
plt.ylabel('North->')
plt.rcParams['figure.figsize']=(40,20)
plt.show()

---

一维有边界的随机游走问题

• 下面先对一维双边界随机游走问题进行求解：设初始位置为
• $x=n$，边界为 $x=0$ 和 $ x=w$，其中 $0<=n<=w$，$n、w$ 为整数。游走者每个单位时间移动一次，向左、向右移动的概率都为 $1/2$，达到边界后停止移动。

　　若用 $S_n$ 表示初始位置为 $x=n$ 时最终落入边界 $x=0$ 的概率。显然我们会有 $S_0=1$ 和 $S_w=0$，即初始位置为边界的情况。若 $0<n<w$，则考虑其下一次移动。有 1/2 的概率向左到达 $n-1$，有$1/2$ 的概率向右到达 $n+1$。 则由全概率公式可得

　　　　$S_n =\frac{1}{2} S_{n+1}+\frac{1}{2} S_{n-1}$　　　　
　　整理得到

　　　　$S_{n+1}=2 S_{n}-S_{n-1}$

　　利用

　　　　$S_{n+1}-S_{n}=S_{n}-S_{n-1}$

　　可得

　　　　$S_{n}-S_{n-1}=\cdots=S_{1}-S_{0}=k$

　　累加法可得

　　　　$S_{n}=k n+S_{0}$

 　　由 $S_0=1，S_w=0$，可得

　　　　$S_{n}=1-\frac{1}{w} n=\frac{w-n}{w}$ 同理，$T_n$ 初始位置为 $x=n$ 时最终落入边界 $x=w$ 的概率，可得 $T_n=n/w$。 对于单边界情况，可以令 $w$ 趋于正无穷得到，即可得 $S_n=1，T_n=0$。

---

全局最优化的方法：随机游走算法

　　梯度下降法方法对于求解精度不高的情况是实用的，可以用局部极小值近似替代全局最小值点。但是当要求精确求解全局最小值时，梯度下降法就不适用了，需要采用其他的办法求解。常见的求解全局最优的办法有拉格朗日法、线性规划法、以及一些人工智能算法比如遗传算法、粒子群算法、模拟退火算法等(可以参见我之前的博客)。而今天要讲的是一个操作简单但是不易陷入局部极小值的方法：随机游走算法。

　　随机游走算法操作步骤

　　设 $f(x)$ 是一个含有 $n$ 个变量的多元函数， $x=\left(x_{1}, x_{2}, \ldots, x_{n}\right)$  为 $n$ 维向量。
　　1. 给定初始迭代点 $ x$ ，初次行走步长 $ \lambda$ ，控制精度 $ \epsilon$$(\epsilon$ 是一个非常小的正数, 用于控制结束算法 $ )$ 。
　　2. 给定迭代控制次数 $ N$，$k$ 为当前迭代次数，置 $ k=1$ 。
　　3. 当 $ k<N$ 时，随机生成一个$ (-1,1) $ 之间的 $ n$ 维向量 $ u=\left(u_{1}, u_{2}, \cdots, u_{n}\right),\left(-1<u_{i}<1, i=1,2, \cdots, n\right) $，并将其标准化得到 $ u^{\prime}=\frac{u}{\sqrt{\sum_{i=1}^{n} 　　u_{i}^{2}}} $ 。 令 $ x_{1}=x+\lambda u^{\prime}$ ，完成第一步游走。
　　4. 计算函数值，如果 $ f\left(x_{1}\right)<f(x)$，即找到了一个比初始值好的点，那么 $ k$ 重新置为 $1$，将 $ x_{1}$ 变为 $ x$，回到第2步；否则 $ k=k+1$，回到第3步。
　　5. 如果连续 $ N$ 次都找不到更优的值，则认为，最优解就在以当前最优解为中心, 当前步长为半径的 $ N$ 维球内(如果是三维，则刚好是空 间中的球体)。此时，如果 $\lambda<\epsilon$ ， 则结束算法；否则，令 $\lambda=\frac{\lambda}{2} $，回到第1步，开始新一轮游走。

---

图上的随机游走

　　图上的 Random  Walk 是指给定一个图和一个出发点，随机地选择一个邻居结点，移动到邻居结点上，然后把当前结点作为出发点，重复以上过程。那些被随机选出的结点序列就构成了一个在图上的 Random Walk 过程，如下图所示。

　　　　

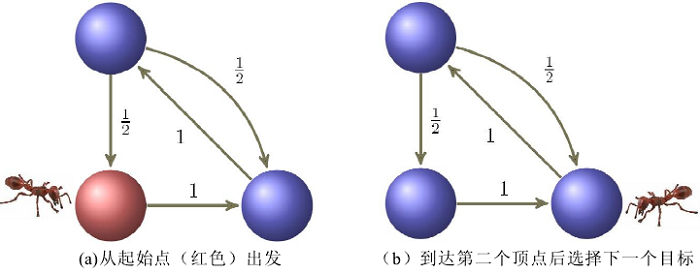
　　早期的搜索引擎例如Yahoo！使用的是关键词匹配技术，其性能容易受到关键词频率的欺骗，所以搜索效果不是很好。但是到1998年Jon Kleinberg 提出了HITS[17]算法，以及Sergey Brin  和 Larry Page 提出了 PageRank[18]算法之后，搜索的正确率就得到了巨大的改观，其原因就是这两种技术都建立在共同理论支柱就是图上的 Random  Walk上。

　　Random  Walk 是随机过程（Stochastic  Process）的一个重要组成部分，通常描述的是最简单的一维 Random  Walk 过程。下面给出一个例子来说明：考虑在数轴原点处有一只蚂蚁，它从当前位置(记为x（t） )出发，在下一个时刻( x（t+1）)以 的概率向前走一步(即 x（t+1）= x（t）+1)，或者以 的概率向后走一步(即 x（t+1）= x（t）-1)，这样蚂蚁每个时刻到达的点序列 就构成一个一维随机游走过程。

　　本质上 Random  Walk 是一种随机化的方法，在实际上生活中，例如醉汉行走的轨迹、花粉的布朗运动、证券的涨跌等都与 Random  Walk 有密不可分的关系。Random Walk已经被成功地应用到数学，物理，化学，经济等各种领域。当前研究者们已经开始将 Random  Walk 应用到信息检索、图像分割等领域，并且取得了一定的成果，其中一个突出的例子就是 Brin 和 Page 利用基于 Random Walk 的 PageRank 技术创建了 Google 公司。

　　相关理论

　　马尔科夫链：t+1时刻的状态只与t时刻有关，也就是只与上一步状态有关，如果从i到j的转移概率与时间无关称为齐时马尔科夫链，否则称为非齐时马尔科夫链。

---