论文解读（PCL）《Prototypical Contrastive Learning of Unsupervised Representations》

论文信息

论文标题：Prototypical Contrastive Learning of Unsupervised Representations
论文作者：Junnan Li, Pan Zhou, Caiming Xiong, Steven C.H. Hoi
论文来源：2020, ICLR
论文地址：download 
论文代码：download 

1 Introduction

　　本文提出了一个将对比学习与聚类联系起来的无监督表示学习方法：Prototypical Contrastive Learning (PCL) 。该方法解决了逐实例（instance wise）对比学习的基本缺陷。PCL不仅可以为实例判别任务学习底层（low level）特征，更重要的是它将通过聚类发现的语义结构编码到学习的嵌入空间中。

　　在 PCL 中，作者引入了一个「原型」作为由相似图像形成的簇的质心。将每个图像分配给不同粒度的多个原型（每个实例的原型是其增强特征）。训练的目标是使每个图像嵌入更接近其相关原型，这是通过最小化一个 ProtoNCE 损失函数来实现的。

　　　　　　　　

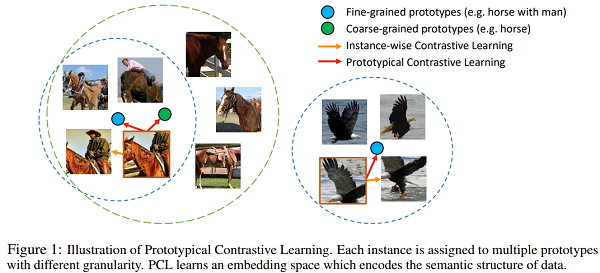
　　fine-grained：细粒度，fine-grained classification是细粒度的图像分类，类内细分。
　　coarse-grained：粗粒度，coarse-grained classification是粗粒度的图像分类，类间细分。

---

Part2 介绍

2.1 实例对比学习

　　优点：本质上，实例对比学习会产生嵌入空间（embedding space），其中所有实例都很好地分离，并且每个实例都是局部平滑的。

　　缺点：

1. 1. 利用低层线索就可以区分不同的实例，因此学习到的嵌入不一定捕获高级语义（有用的语义知识）。 实例分类的准确性通常迅速上升到高水平（10 个时期内> 90％）并且进一步训练提供的信息信号有限。 
   2. 不鼓励表示对数据的语义结构进行编码。原因：实例对比学习将两个样本视为负对，只要它们来自不同的实例，而不管它们的语义相似性。由于生成了数千个负样本以形成对比损失，导致许多负对共享相似的语义但在嵌入空间中被不希望地分开，这一事实放大了这一点。

　　许多最先进的对比学习方法(例如 MoCo 和 SimCLR )都是基于实例辨别的任务。

　　实例判别训练一个网络来分类两个图像是否来自同一个源图像，如 Figure 1 (a)所示。该网络将每个图像裁剪投影到一个嵌入中，并将同源的嵌入彼此拉近，同时将不同源的嵌入分开。通过解决实例判别任务，期望网络学习到一个有用的图像表示。

 

　　　　　　　　　

　　Q：局部平滑？

　　A：个人理解：解决零概率问题。为避免在计算中某情况概率计算为0，但实际上是存在（>0）的的情况。参考

　　Q：嵌入(Embedding)

　　A：Embedding 是一种分布式表示方法，即把原始输入数据分布地表示成一系列特征的线性组合。Embedding 的本质是“压缩”，用较低维度的 k 维特征去描述有冗余信息的较高维度的 n 维特征，也可以叫用较低维度的 k 维空间去描述较高维度的 n 维空间。在思想上，与线性代数的主成分分析 PCA，奇异值分解 SVD 异曲同工。

　　NLP 中的 Embedding，每一个词都被表示成指定维度（比如 300 或者 768）的向量，每一个维度对应词的一种语义特征。在NLP中，显然不可能从语言学角度先验地知道每一个维度具体表示哪一种语义特征，也没法知道一个Token对应的特征值具体是多少，所以这就需要通过语言模型训练来得到对应的值。

2.2 原型对比学习

　　为每个实例分配了几个不同粒度的原型，并构建了一个对比损失，与其他原型相比，它强制样本的嵌入与其对应的原型更相似（$\Longrightarrow $ 在高层次上，PCL 的目标是找到给定观测图像的最大似然估计模型参数）。 在实践中，可以通过对嵌入进行聚类来找到原型。

　　作者将原型对比学习制定为一种期望最大化 (EM) 算法，其目标是通过迭代地逼近和最大化对数似然函数来找到最能描述数据分布的深度神经网络 (DNN) 的参数。

　　具体来说，引入原型作为额外的潜在变量，并通过执行 k 均值聚类来估计它们在 E 步骤中的概率。在 M 步中，通过最小化我们提出的对比损失来更新网络参数，即 ProtoNCE。

---

Part3 PCL

3.1 实例对比学习Preliminaries

　　给定训练数据集  $X=\left\{x_{1}, x_{2}, \ldots, x_{n}\right\} $ 即 $n$ 张 image，无监督表示学习网络  $f_{\theta}$  将  $X$  映射到  $V=\left\{v_{1}, v_{2}, \ldots, v_{n}\right\}, v_{i}$  是  $x_{i}$  的最佳表示，该目标通过逐实例 (instance wise) 的对比学习得到

　　　　$\mathcal{L}_{\mathrm{InfoNCE}}=\sum \limits _{i=1}^{n}-\log \frac{\exp \left(v_{i} \cdot v_{i}^{\prime} / \tau\right)}{\sum_{j=0}^{r} \exp \left(v_{i} \cdot v_{j}^{\prime} / \tau\right)}$

　　其中 $v_{i}^{\ \prime}$ 和 $v_{i}$ 是实例 $i$ 的正样本对，$v_{j}^{\ \prime}$ 包含了一个正样本嵌入，$r$ 个负样本嵌入。

　　Review：MoCo　　　

　　　　　

• $v_{i}=f_{\theta}\left(x_{i}\right)$，其中 $f_{\theta}$ 是 encoder 。$v_{i}$ 是从 encoder 中得到。
• $v_{i}^{\ \prime}=f_{\theta^{\ \prime}}\left(x_{i}\right)$ ，其中 $\theta^{\prime}$ 是 $\theta$ 的移动平均（moving average） ，$f_{\theta^{\ \prime}} $ 为 momentum encoder。$v_{i}^{\ \prime}$  和 $v_{j}^{\ \prime}$ 是通过  momentum encoder 获得。

　　对于每个 batch ：

1. 随机增强出 $x^{q} 、 x^{k} $ 两种 view ;
2. 分别用 $f_{q} $ , $ f_{k} $ 对输入进行编码得到归一化的 $q $ 和 $ \mathrm{k} $ , 并去掉 $\mathrm{k} $ 的梯度更新 ;
3. 将 $\mathrm{q} $ 和 $\mathrm{k} $ 中的唯一一个正例做点积得 cosine相似度 ($\mathrm{N  \times } 1$) , 再将 $\mathrm{q}$ 和队列中存储的K个负样本做点积得 cosine相似度 ($\mathrm{N \times K}$) , 拼接起来的到 $\mathrm{N \times }(1+\mathrm{K}) $ 大小 的矩阵, 这时第一个元素就是正例，直接计算交叉摘损失, 更新 $f_{q}$ 的参数；
4. 动量更新 $f_{k} $ 的参数 $\theta_{k}$ ： $ \theta_{\mathrm{k}} \leftarrow m \theta_{\mathrm{k}}+(1-m) \theta_{\mathrm{q}}$；
5. 将 $ \mathrm{k}$ 加入队列，把队首的旧编码出队，负例最多时有 65536 个。

3.2 PCL

　　在PCL中，用 prototype $c$ 代替  $v^{\prime }$，用 per-prototype 集中程度估计（concentration estimation）代替 $\tau$，PCL结构图如下

 　　　　　　　　

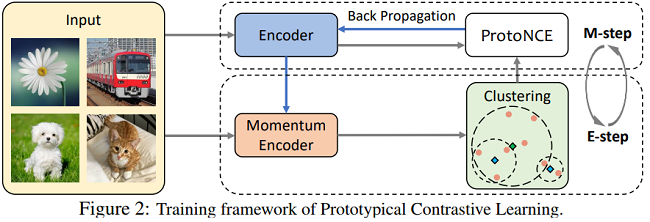
　　在 PCL 中，引入了一个 原型（prototype）作为由相似图像形成的簇的质心。将每个图像分配给不同粒度的多个原型。训练的目标是使每个图像嵌入更接近其相关原型，这是通过最小化一个 ProtoNCE 损失函数来实现的。

　　PCL 的目标是找到给定观测图像的最大似然估计（MLE）模型参数 $\theta$：

 　　　　$\theta^{*}= \underset{\theta}{arg \  max}  \sum \limits _{i=1}^{n} \log p\left(x_{i} ; \theta\right) $

 　　我们假设观察到的数据 $\left\{x_{i}\right\}_{i=1}^{n}$ 与表示数据原型的潜在变量 $C=\left\{c_{i}\right\}_{i=1}^{k}$ 相关。 这样，我们可以将对数似然函数重写为：

 　　　　$\theta^{*}=\underset{\theta}{\arg \max } \sum \limits _{i=1}^{n} \log p\left(x_{i} ; \theta\right)=\underset{\theta}{\arg \max } \sum \limits_{i=1}^{n} \log \sum \limits_{c_{i} \in C} p\left(x_{i}, c_{i} ; \theta\right) $

 　　由于无法直接优化上式（ $C$ 未知），则根据 Jensen 不等式构建其下界

 　　　　$\sum \limits _{i=1}^{n} \log \sum \limits_{c_{i} \in C} p\left(x_{i}, c_{i} ; \theta\right)=\sum \limits_{i=1}^{n} \log \sum \limits_{c_{i} \in C} Q\left(c_{i}\right) \frac{p\left(x_{i}, c_{i} ; \theta\right)}{Q\left(c_{i}\right)} \geq \sum \limits_{i=1}^{n} \sum \limits_{c_{i} \in C} Q\left(c_{i}\right) \log \frac{p\left(x_{i}, c_{i} ; \theta\right)}{Q\left(c_{i}\right)}$

 　　其中 $Q\left(c_{i}\right)$ 表示原型 c  上的某种分布，这里 $\sum \limits _{c_{i} \in C} Q\left(c_{i}\right)=1$ 。

　　为了让不等式取等号需要 $\frac{p\left(x_{i}, c_{i} ; \theta\right)}{Q\left(c_{i}\right)}$ 为常数

　　　　$\frac{p\left(x_{i}, c_{i} ; \theta\right)}{Q\left(c_{i}\right)}=m$

　　　　$\sum \limits _{c_{i}} p\left(x_{i}, c_{i} ; \theta\right)=\sum \limits _{c_{i}} Q\left(c_{i}\right) m$

　　　　$p\left(x_{i} ; \theta\right)=m$

 　　进一步使用上述结论 $p\left(x_{i} ; \theta\right)=m$ ，带入 $\frac{p\left(x_{i}, c_{i} ; \theta\right)}{Q\left(c_{i}\right)}=m$ 可得

　　　　$\frac{p\left(x_{i}, c_{i} ; \theta\right)}{Q\left(c_{i}\right)}=m$

　　　　$Q\left(c_{i}\right)=\frac{p\left(x_{i}, c_{i} ; \theta\right)}{m}$

　　　　$Q\left(c_{i}\right)=\frac{p\left(x_{i}, c_{i} ; \theta\right)}{p\left(x_{i} ; \theta\right)}$

　　　　$Q\left(c_{i}\right)=p\left(c_{i} ; x_{i} , \theta\right)$

　　上式为E步所需计算的式子(即得到 $Q\left(c_{i}\right)$) ，M步固定 $Q\left(c_{i}\right)$(看作常数)最大化下界函数，由于 $Q\left(c_{i}\right)$ 被看作常数，则有

　　　　$\underset{\theta}{\arg \max } \sum \limits _{i=1}^{n} \sum \limits_{c_{i} \in C} Q\left(c_{i}\right) \log \frac{p\left(x_{i}, c_{i} ; \theta\right)}{Q\left(c_{i}\right)}=\underset{\theta}{\arg \max } \sum \limits_{i=1}^{n} \sum \limits_{c_{i} \in C} Q\left(c_{i}\right) \log p\left(x_{i}, c_{i} ; \theta\right)$

• E Step

 　　该步骤目的是估计 $p\left (c_{i} ; x_{i} , \theta\right)$，作者在 $v_{i}^{\  \prime}=f_{\theta^{ \  \prime}}\left(x_{i}\right)$ 特征上运行k-means算法，将 prototype $c_i$ 看作第 $i$ 个簇的中心点，作者定义

 　　　　$p\left(c_{i} ; x_{i} , \theta\right)=\left\{\begin{array}{lr} 1 & \text { if } x_{i} \text { belongs to cluster } c_{i} \\ 0 & \text { otherwise } \end{array}\right.$

• M Step

　　基于E步，现在可以最大化下界函数

　　$\sum \limits _{i=1}^{n} \sum \limits _{c_{i} \in C} Q\left(c_{i}\right) \log p\left(x_{i}, c_{i} ; \theta\right)=\sum \limits _{i=1}^{n} \sum \limits _{c_{i} \in C} p\left(c_{i} ; x_{i}, \theta\right) \log p\left(x_{i}, c_{i} ; \theta\right) =\sum \limits _{i=1}^{n}\sum \limits_{c_{i} \in C} \mathbb{1}\left(x_{i} \in c_{i}\right) \log p\left(x_{i}, c_{i} ; \theta\right) $

　　作者假设每个 cluster $c_i$ 的先验分布都满足均匀分布，因为我们没有提供任何样本，即

　　　　$p\left(x_{i}, c_{i} ; \theta\right)=p\left(x_{i} ; c_{i}, \theta\right) p\left(c_{i} ; \theta\right)=\frac{1}{k} \cdot p\left(x_{i} ; c_{i}, \theta\right)$

　　作者假设每个prototype周围的分布是各向同性的高斯分布，则可得出

　　　　$p (x_{i} ; c_{i}, \theta )=\exp  ({\large \frac{- (v_{i}-c_{s} )^{2}}{2 \sigma_{s}} } ) / \sum \limits _{j=1}^{k} \exp  ({\large \frac{- (v_{i}-c_{j} )^{2}}{2 \sigma_{j}^{2}} } )$

　　其中  $x_{i} \in c_{s}, v_{i}=f_{\theta}\left(x_{i}\right) $, 如果给  $c$  和  $v$  都施加 $\ell_{2}$ 正则化，则  $(v-c)^{2}=2-2 v \cdot c$ 。

　　综合上述内容，M步需要优化的式子如下

　　　　$\theta^{*}=\underset{\theta}{\arg \min } \sum \limits _{i=1}^{n}-\log {\large \frac{\exp \left(v_{i} \cdot c_{s} / \phi_{s}\right)}{\sum_{j=1}^{k} \exp \left(v_{i} \cdot c_{j} / \phi_{j}\right)}} $

　　其中 $\phi$ 表示原型周围特征分布的集中程度。

　　发现上式与 InfoNCE 相似，因此 $\operatorname{lnfoNCE}$ 可以看作最大对数似然估计的特例：$v_{i}$ 的 prototype 是与其相同实例的增强特征 $v_{i}^{\prime}$  (即 $c=v^{\prime}$ ) ，并且每个实例周围的特征分布集中程度 (concentration) 都是固定的（即 $\phi=\tau$ )。

　　在实际实现中，作者采用与NCE相同的方法，采样 r 个负 prototype 来计算正则化项。为了能对 编码层次结构的 prototype 有更 robust 的概率估计，作者用不同的聚类数量 $ K=\left\{k_{m}\right\}_{m=1}^{M}$ 进行 M 次聚类，此外作者增加 InfoNCE loss 来保持局部光滑性并引导聚类。最终的目标函数 ProtoNCE 如下

　　　　$\mathcal{L}_{\text {ProtoNCE }}=\sum \limits _{i=1}^{n}- {\large (\log \frac{\exp  (v_{i} \cdot v_{i}^{\prime} / \tau )}{\sum \limits_{j=0}^{r} \exp  (v_{i} \cdot v_{j}^{\prime} / \tau )}} +\frac{1}{M} \sum \limits_{m=1}^{M} \log {\large \frac{\exp  (v_{i} \cdot c_{s}^{m} / \phi_{s}^{m} )}{\sum \limits_{j=0}^{r} \exp  (v_{i} \cdot c_{j}^{m} / \phi_{j}^{m} )} )} $

3.3 Concentration estimation 

　　由于不同 prototype 周围的 embedding 的分布都有不同程度的集中程度（concentration），因此作者使用 $\phi$ 对其估计（ $\phi$ 值越小集中程度越大），我们使用同一簇 $c$ 内的 momentum 特征 $\left\{v_{z}^{\prime}\right\}_{z=1}^{Z}$  计算 $\phi$ 。

　　我们期望 $\phi$ 在以下两个情况时值很小：

• $v_{z}^{\prime}$ 和 $c$ 之间的平均距离很小。
• 簇包含的很多特征点（即 $Z$ 很大）。

 　　因此定义 $\phi$ 为

　　　　$\phi=\frac{\sum \limits _{z=1}^{Z}\left\|v_{z}^{\prime}-c\right\|_{2}}{Z \log (Z+\alpha)}$

 　　其中，$\alpha$ 为平滑变量保证小簇不会出现过大的 $\phi$ ，我们对每组 prototype （$C^M$ 组）的 $\phi$ 进行归一化，使其为 $\tau$ 的均值。

3.4 算法

　　　　　　　　

　　　　　　　　

---

Part4 实验

4.1 Low-shot  image classification

　　　　　　　　

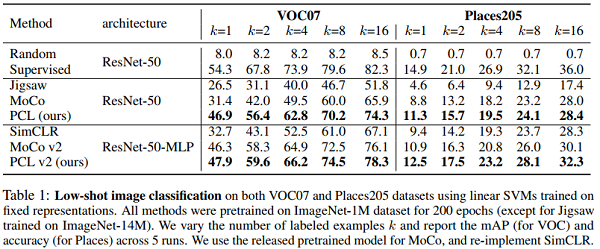
 　　实验在VOC07和Places205数据集上利用框架学到的表示使用 SVM 做图像分类实验。左 mAP、右ACC。

4.2 Semi-supervised image classification

　　执行半监督学习实验来评估学习的表示是否可以为微调提供良好的基础。（半监督）

　　　　　　　　

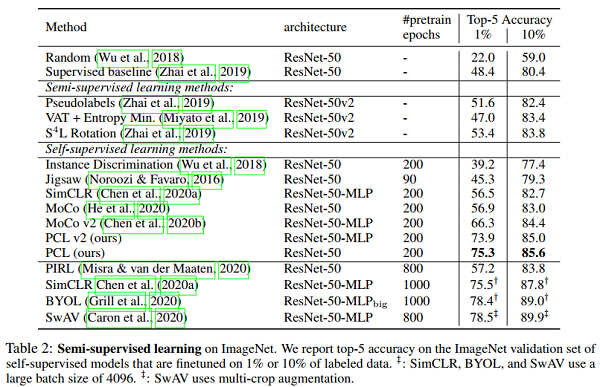
4.3 IMAGE CLASSIFICATION BENCHMARKS

　　　　　　　　

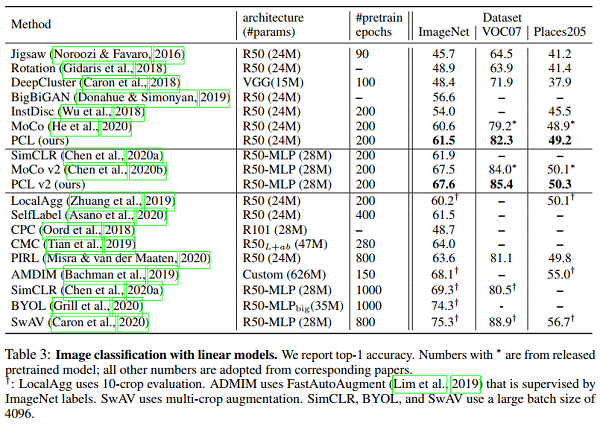
　　1-crop和10-crop顾名思义就是进行1次和10次裁剪。举个例子输入图像是256×256的，网络训练所需图像是224×224的。

　　1-corp是从256×256图像中间位置裁一个224×224的图像进行训练，而10-corp是先从中间裁一个224×224的图像，然后从图像左上角开始，横着数224个像素，竖着数224个像素开始裁剪，同样的方法在右上，左下，右下各裁剪一次。就得到了5张224*224的图像，镜像以后再做一遍，总共就有10张图片了。

4.4 CLUSTERING EVALUATION

　　　　　　　　

　　　　　　　

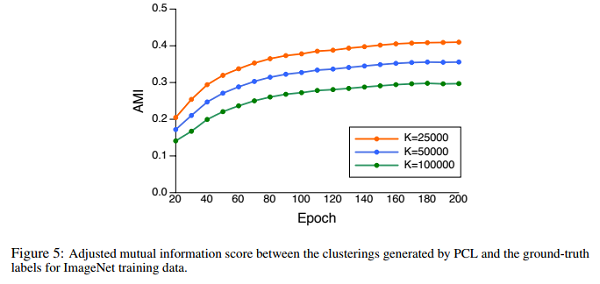
 　　AMI 用来衡量两个分布的吻合程度，取值范围[-1,1]，值越大聚类效果与真实情况越吻合。

4.5 OBJECT DETECTION

　　　　　　　　

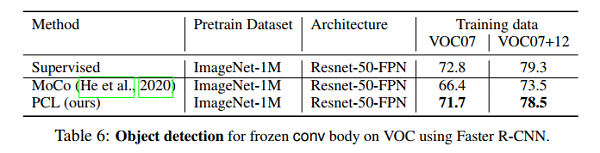
-----------------------------------------------完-----------------------------------------------