机器学习——高等数学

1 导数定义

　　导数和微分的概念

　　　　$f'({x_0})=\underset{\bigtriangleup x \longrightarrow 0}{lim}      \ {\large \frac{f(x)-f(x_0)}{x-{{x_0}}}} $

　　或者：

　　　　$f'({x_0})=\underset{ x \longrightarrow x_0}{lim} \  {\large \frac{f(x)-f(x_0)}{x-{{x_0}}}} $

2 左右导数导数的几何意义和物理意义

　　函数 $f(x)$ 在 $x_0$ 处的左、右导数分别定义为：

　　左导数：

　　　　${{f'_-}}({x_0})=\underset{\Delta x \longrightarrow 0^{-}}{lim} \  {\large \frac{f({x_0}+\Delta x)-f({x_0})}{\Delta x}}  =\underset{ x \longrightarrow x_0^{-}}{lim}\  {\large \frac{f(x)-f({x_0})}{x-{x_0}}} ,\quad(x={x_0}+\Delta x)$

　　右导数：

　　　　${{f'_+}}({x_0})=\underset{\Delta x \longrightarrow 0^{+}}{lim} \ {\large \frac{f({x_0}+\Delta x)-f({x_0})}{\Delta x}} =\underset{ x \longrightarrow x_0^{+}}{lim}\  {\large \frac{f(x)-f({x_0})}{x-{x_0}}} $

3 函数的可导性与连续性之间的关系

　　Th1：函数 $f(x)$ 在 $x_0$ 处可微 $\Leftrightarrow f(x)$ 在 $x_0$ 处可导。

　　Th2：若函数在点 $x_0$ 处可导，则 $y=f(x)$ 在点 $x_0$ 处连续，反之则不成立。即函数连续不一定可导。

　　Th3：${f}'({x_0})$ 存在 $\Leftrightarrow {{f'_-}}({x_0})={{f'_+}}({{x}_{0}})$

4 平面曲线的切线和法线

　　切线方程 : $y-{y_0}=f'({x_0})(x-{{x}_{0}})$

　　法线方程：$y-{y_0}=-\frac{1}{{\large f'({x_0})} }(x-{x_0}),\quad f'({x_0})\ne 0$

5 四则运算法则

　　设函数 $u=u(x)，v=v(x)$ 在点 $x$ 可导则

　　$(u\pm v{)}'={u}'\pm {v}'$　　$d(u\pm v)=du\pm dv$

　　$(uv{)}'=u{v}'+v{u}'$　　$d(uv)=udv+vdu$

　　$({\large \frac{u}{v})'} ={\large \frac{v{u}'-u{v}'}{{{v}^{2}}}} (v\ne 0)$　　${\large d(\frac{u}{v})} ={\large \frac{vdu-udv}{{{v}^{2}}}} $

6 基本导数与微分表

　　(1) $y=c$（常数）

　　　　 ${y}'=0$　　$dy=0$

　　(2) $y={{x}^{\alpha }}$($\alpha $为实数)

　　　　${y}'=\alpha {{x}^{\alpha -1}}$　　$dy=\alpha {{x}^{\alpha -1}}dx$

　　　　

　　(3) $y={{a}^{x}}$

　　　　${y}'={{a}^{x}}\ln a$　　$dy={{a}^{x}}\ln adx$

　　　　特例: $({{{e}}^{x}}{)}'={{{e}}^{x}}$ $d({{{e}}^{x}})={{{e}}^{x}}dx$

　　　　

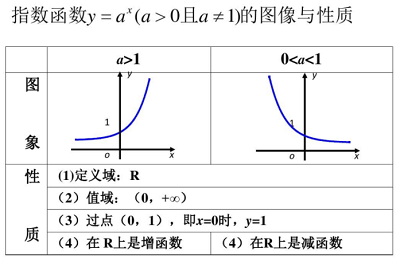
　　(4) $y={{\log }_{a}}x$　　${y}'=\frac{1}{x\ln a}$

　　　　$dy=\frac{1}{x\ln a}dx$

　　　　特例：$y=\ln x$ $(\ln x{)}'=\frac{1}{x}$　　$d(\ln x)=\frac{1}{x}dx$

　　　　

　　(5) $y=\sin x$

　　　　${y}'=\cos x$　　$d(\sin x)=\cos xdx$

　　　　

　　(6) $y=\cos x$

　　　　${y}'=-\sin x$　　$d(\cos x)=-\sin xdx$

　　　　

　　(7) $y=\tan x$

　　　　${y}'={\large \frac{1}{{{\cos }^{2}}x}} ={{\sec }^{2}}x$　　$d(\tan x)={{\sec }^{2}}xdx$

　　　　

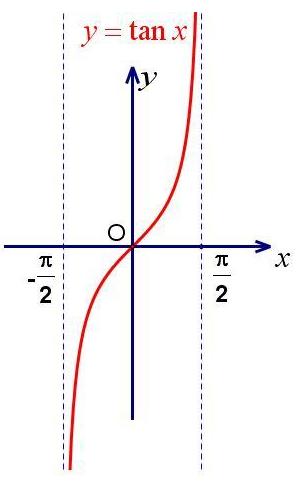
　　(8) $y=\cot x$　　

　　　　${y}'={\large -\frac{1}{{{\sin }^{2}}x}} =-{{\csc }^{2}}x$　　$d(\cot x)=-{{\csc }^{2}}xdx$

　　　　

　　(9) $y=\sec x =\sec x = {\large \frac{1}{\cos x} } $　　

　　　　${y}'=\sec x\tan x$　　$d(\sec x)=\sec x\tan xdx$

　　　　

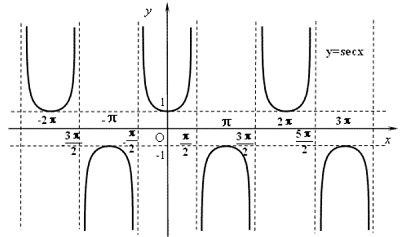
　　(10) $y=\csc x ={\large  \frac{1}{\sin x}}  $

　　　　${y}'=-\csc x\cot x$　　$d(\csc x)=-\csc x\cot xdx$

　　　　

　　(11) $y=\arcsin x$

　　　　${y}'={\large \frac{1}{\sqrt{1-{{x}^{2}}}}} $　　$d(\arcsin x)=\frac{1}{\sqrt{1-{{x}^{2}}}}dx$

　　　　

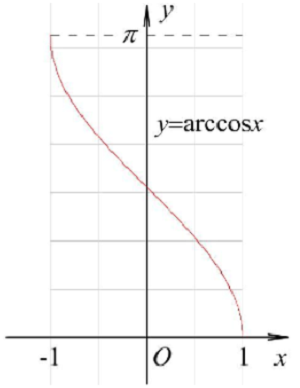
　　(12) $y=\arccos x$

　　　　${y}'=-\frac{1}{\sqrt{1-{{x}^{2}}}}$　　$d(\arccos x)={\large -\frac{1}{\sqrt{1-{{x}^{2}}}}} dx$

　　　　

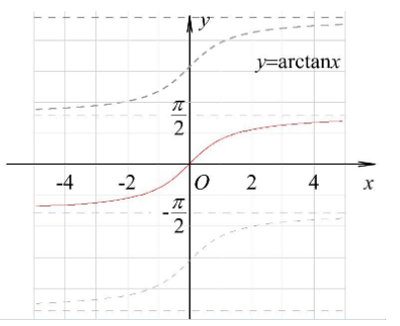
　　(13) $y=\arctan x$

　　　　${y}'={\large \frac{1}{1+{{x}^{2}}}} $　　$d(\arctan x)={\large \frac{1}{1+{{x}^{2}}}} dx$

　　　　

　　(14) $y=\operatorname{arc}\cot x$

　　　　${y}'={\large -\frac{1}{1+{{x}^{2}}}} $　　$d(\operatorname{arc}\cot x)={\large -\frac{1}{1+{{x}^{2}}}} dx$

　　　　

　　(15) $y=shx$

　　　　${y}'=chx$　　$d(shx)=chxdx$

　　(16) $y=chx$

　　　　${y}'=shx$　　$d(chx)=shxdx$

7 复合函数，反函数，隐函数以及参数方程所确定的函数的微分法

　　(1) 反函数的运算法则：设 $y=f(x)$ 在点 $x$ 的某邻域内单调连续，在点 $x$ 处可导且 ${f}'(x)\ne 0$，则其反函数在点 $x$ 所对应的 $y$ 处可导，并且有  ${\large \frac{dy}{dx}=\frac{1}{\frac{dx}{dy}}} $。

　　(2) 复合函数的运算法则：若 $\mu =\varphi (x)$ 在点 $x$ 可导，而 $y=f(\mu )$ 在对应点 $\mu $ ( $\mu =\varphi (x)$ ) 可导，则复合函数 $y=f(\varphi (x))$在点$x$可导,且${y}'={f}'(\mu )\cdot {\varphi }'(x)$ 。

　　(3) 隐函数导数 $\frac{dy}{dx}$ 的求法一般有三种方法：

1. 1. 方程两边对 $x$ 求导，要记住 $y$ 是 $x$ 的函数，则 $y$ 的函数是 $x$ 的复合函数。例如 $\frac{1}{y}$，${{y}^{2}}$，$ln y$， ${{{e}}^{y}}$ 等均是 $x$ 的复合函数. 对 $x$ 求导应按复合函数连锁法则做。
   2. 公式法。由 $F(x,y)=0$ 知 $\frac{dy}{dx}=-\frac{{{{{F}'}}{x}}(x,y)}{{{{{F}'}}{y}}(x,y)}$,其中，${{{F}'}{x}}(x,y)$， ${{{F}'}{y}}(x,y)$分别表示$F(x,y)$对$x$和$y$的偏导数。
   3. 利用微分形式不变性。

8.常用高阶导数公式

　　（1）$({{a}^{x}})^{(n)}={{a}^{x}}{{\ln }^{n}}a\quad (a>{0})\quad \quad ({{{e}}^{x}})^{(n)}={e}{{,}^{x}}$

　　（2）$(\sin kx{)}^{(n)}={{k}^{n}}\sin (kx+n\cdot \frac{\pi }{{2}})$

　　（3）$(\cos kx{)}^{(n)}={{k}^{n}}\cos (kx+n\cdot \frac{\pi }{{2}})$

　　（4）$({{x}^{m}})^{(n)}=m(m-1)\cdots (m-n+1){{x}^{m-n}}$

　　（5）$(\ln x)^{(n)}={{(-{1})}^{(n-{1})}}\frac{(n-{1})!}{{{x}^{n}}}$

　　（6）莱布尼兹公式：若 $u(x),,v(x)$ 均 $n$ 阶可导，则 ${{(uv)}^{(n)}}=\sum\limits_{i={0}}^{n}{c_{n}^{i}{{u}^{(i)}}{{v}^{(n-i)}}}$，其中 ${{u}^{({0})}}=u$，${{v}^{({0})}}=v$

9.微分中值定理

　　Th1：(费马定理)

　　若函数 $f(x)$ 满足条件：

　　(1)函数 $f(x)$ 在 ${x_0}$ 的某邻域内有定义，并且在此邻域内恒有 $f(x)\le f({x_0})$ 或 $f(x)\ge f({{x}_{0}})$,

　　(2) $f(x)$ 在 ${x_0}$ 处可导,则有 ${f}'({x_0})=0$

　　Th2：(罗尔定理)

　　设函数 $f(x)$ 满足条件：

　　(1)在闭区间 $[a,b]$ 上连续；

　　(2)在 $(a,b)$ 内可导；

　　(3)$f(a)=f(b)$；

　　则在 $(a,b)$内一存在个 $\xi $，使 ${f}'(\xi )=0$

　　Th3: (拉格朗日中值定理)

　　设函数 $f(x)$ 满足条件：

　　(1)在 $[a,b]$ 上连续；

　　(2)在 $(a,b)$ 内可导；

　　则在 $(a,b)$ 内一存在个 $\xi $，使 ${\large \frac{f(b)-f(a)}{b-a}} ={f}'(\xi )$

　　Th4: (柯西中值定理)

　　设函数 $f(x)$，$g(x)$ 满足条件：

　　(1) 在$[a,b]$上连续；

　　(2) 在 $(a,b)$ 内可导且 ${f}'(x)$ ，${g}'(x)$ 均存在，且 ${g}'(x)\ne 0$

　　则在 $(a,b)$ 内存在一个$\xi $，使 ${\large \frac{f(b)-f(a)}{g(b)-g(a)}} ={\large \frac{{f}'(\xi )}{{g}'(\xi )}} $

10 洛必达法则

　　法则 Ⅰ ( $\frac{0}{0}$ 型)

　　设函数 $f\left( x \right),g\left( x \right)$满足条件：

　　(1) $\underset{x \to x_0}{lim}  \   f\left( x \right)=0,\ \underset{x \to x_0}{lim}  \  g\left( x \right)=0$；

　　(2) $f\left( x \right),g\left( x \right)$ 在 ${x_0}$ 的邻域内可导，(在 ${x_0}$ 处可除外) 且 ${g}'\left( x \right)\ne 0$；

　　(3) $\underset{x \to x_0}{lim}  \  \frac{{f}'\left( x \right)}{{g}'\left( x \right)}$ 存在 (或$\infty $)。

　　则：$\underset{x \to x_0}{lim}  \ \frac{f(x)}{g(x)} =\underset{x \to x_0}{lim}  \ \frac{f'(x)}{g'(x)} $。

　　法则 ${{I}'}$  ($\frac{0}{0}$型)

　　设函数 $f\left( x \right),g\left( x \right)$

　　满足条件：

　　(1) $\underset{x \to x_0}{lim}  \ f\left(x \right)=0,\underset{x \to x_0}{lim}  \ g\left(x \right)=0$;

　　(2) 存在一个 $X>0$ ，当 $\left| x \right|>X$ 时，$f\left( x \right),g\left( x \right)$ 可导，且 ${g}'\left( x \right)\ne 0$；$\underset{x \to x_0}{lim}  \ \frac{{f}'\left(x \right)}{{g}'\left(x \right)}$ 存在 (或 $\infty $) 。

　　则：$\underset{x \to x_0}{lim}  \ \frac{f\left( x \right)}{g\left( x \right)}=\underset{x \to x_0}{lim}  \ \frac{{f}'\left( x \right)}{{g}'\left( x \right)}$。

　　法则 Ⅱ( $\frac{\infty }{\infty }$ 型)

　　设函数 $f\left( x \right),g\left( x \right)$ 满足条件：

　　(1) $\underset{x \to x_0}{lim}  \ f\left( x \right)=\infty ,\underset{x \to x_0}{lim}  \ g\left( x \right)=\infty$；

　　(2) $f\left( x \right),g\left( x \right)$ 在 ${x_0}$  的邻域内可导(在 ${x_0}$ 处可除外)且${g}'\left( x \right)\ne 0$；

　　(3) $\underset{x \to x_0}{lim}  \ \frac{{f}'\left( x \right)}{{g}'\left( x \right)}$存在(或$\infty$)。

　　则

　　$\underset{x \to x_0}{lim}  \ \frac{f\left( x \right)}{g\left( x \right)}=\underset{x \to x_0}{lim}  \ \frac{{f}'\left( x \right)}{{g}'\left( x \right)}$

　　同理法则 ${I{I}'}$($\frac{\infty }{\infty }$ 型)仿法则 ${{I}'}$ 可写出。

11 泰勒公式

　　设函数 $f(x)$ 在点 ${x_0}$ 处的某邻域内具有 $n+1$ 阶导数，则对该邻域内异于 ${x_0}$ 的任意点 $x$，在 ${{x}_{0}}$ 与 $x$ 之间至少存在 一个 $\xi$ ，使得：

　　　　$f(x)=f({x_0})+{f}'({x_0})(x-{x_0})+\frac{1}{2!}{f}''({x_0}){{(x-{{x}_{0}})}^{2}}+\cdots+\frac{{{f}^{(n)}}({x_0})}{n!}{{(x-{x_0})}^{n}}+{{R}_{n}}(x)...........(1)$

　　其中 ${R_n}(x)={\large \frac{{{f}^{(n+1)}}(\xi )}{(n+1)!}} {{(x-{x_0})}^{n+1}}$ 称为 $f(x)$ 在点 ${{x}_{0}}$ 处的 $n$ 阶泰勒余项。

　　令 ${x_0}=0$，则 $n$ 阶泰勒公式 $f(x)=f(0)+{f}'(0)x+\frac{1}{2!}{f}''(0){{x}^{2}}+\cdots +\frac{{{f}^{(n)}}(0)}{n!}{{x}^{n}}+{{R_n}}(x)$

　　其中 ${{R}_{n}}(x)=\frac{{{f}^{(n+1)}}(\xi )}{(n+1)!}{{x}^{n+1}}$，$\xi $ 在 0 与 $x$ 之间。(1) 式称为麦克劳林公式。

　　常用五种函数在${{x}_{0}}=0$处的泰勒公式

　　(1) ${{{e}}^{x}}=1+x+\frac{1}{2!}{{x}^{2}}+\cdots +\frac{1}{n!}{{x}^{n}}+\frac{{{x}^{n+1}}}{(n+1)!}{{e}^{\xi }}$

　　　　或 $=1+x+\frac{1}{2!}{{x}^{2}}+\cdots +\frac{1}{n!}{{x}^{n}}+o({{x}^{n}})$

　　(2) $\sin x=x-\frac{1}{3!}{{x}^{3}}+\cdots +\frac{{{x}^{n}}}{n!}\sin \frac{n\pi }{2}+\frac{{{x}^{n+1}}}{(n+1)!}\sin (\xi +\frac{n+1}{2}\pi )$

　　　　或 $=x-\frac{1}{3!}{{x}^{3}}+\cdots +\frac{{{x}^{n}}}{n!}\sin \frac{n\pi }{2}+o({{x}^{n}})$

　　(3) $\cos x=1-\frac{1}{2!}{{x}^{2}}+\cdots +\frac{{{x}^{n}}}{n!}\cos \frac{n\pi }{2}+\frac{{{x}^{n+1}}}{(n+1)!}\cos (\xi +\frac{n+1}{2}\pi )$

　　　　或 $=1-\frac{1}{2!}{{x}^{2}}+\cdots +\frac{{{x}^{n}}}{n!}\cos \frac{n\pi }{2}+o({{x}^{n}})$

　　(4) $\ln (1+x)=x-\frac{1}{2}{{x}^{2}}+\frac{1}{3}{{x}^{3}}-\cdots +{{(-1)}^{n-1}}\frac{{{x}^{n}}}{n}+\frac{{{(-1)}^{n}}{{x}^{n+1}}}{(n+1){{(1+\xi )}^{n+1}}}$

　　　　或 $=x-\frac{1}{2}{{x}^{2}}+\frac{1}{3}{{x}^{3}}-\cdots +{{(-1)}^{n-1}}\frac{{{x}^{n}}}{n}+o({{x}^{n}})$

　　(5) ${{(1+x)}^{m}}=1+mx+\frac{m(m-1)}{2!}{{x}^{2}}+\cdots +\frac{m(m-1)\cdots (m-n+1)}{n!}{{x}^{n}}$ $+\frac{m(m-1)\cdots (m-n+1)}{(n+1)!}{{x}^{n+1}}{{(1+\xi )}^{m-n-1}}$

　　　　或 ${{(1+x)}^{m}}=1+mx+\frac{m(m-1)}{2!}{{x}^{2}}+\cdots$ $+\frac{m(m-1)\cdots(m-n+1)}{n!}{{x}^{n}}+o({{x}^{n}})$

12 函数单调性的判断

　　Th1：设函数 $f(x)$ 在 $(a,b)$ 区间内可导，如果对 $\forall x\in (a,b)$，都有 $f,'(x)>0$（或$f,'(x)<0$），则函数 $f(x)$ 在 $(a,b)$ 内是单调增加的（或单调减少）

　　Th2：(取极值的必要条件) 设函数 $f(x)$ 在 ${x_0}$ 处可导，且在 ${x_0}$ 处取极值，则 $f,'({{x}_{0}})=0$。

　　Th3：(取极值的第一充分条件) 设函数 $f(x)$ 在 ${x_0}$ 的某一邻域内可微，且 $f,'({x_0})=0$（或 $f(x)$ 在 ${x_0}$ 处连续，但 $f,'({x_0})$ 不存在。）

　　(1)若当 $x$ 经过 ${x_0}$ 时，$f,'(x)$ 由“+”变“-”，则 $f({x_0})$ 为极大值；

　　(2)若当 $x$ 经过 ${x_0}$时，$f,'(x)$ 由“-”变“+”，则 $f({x_0})$ 为极小值；

　　(3)若 $f,'(x)$ 经过 $x={x_0}$ 的两侧不变号，则 $f({x_0})$ 不是极值。

　　Th4：(取极值的第二充分条件)设 $f(x)$ 在点 ${x_0}$ 处有 $f''(x)\ne 0$，且 $f,'({x_0})=0$，则 当 $f','({x_0})<0$ 时，$f({x_0})$ 为极大值； 当 $f','({x_0})>0$ 时，$f({x_0})$ 为极小值。 注：如果 $f','({{x}_{0}})<0$，此方法失效。

13 渐近线的求法

　　(1) 水平渐近线若 $\underset{x \to +\infty }{lim} \ f(x)=b$，或 $\underset{x \to -\infty }{lim} \ f(x)=b$，则 $y=b$ 称为函数 $y=f(x)$ 的水平渐近线。

　　(2) 铅直渐近线若 $\underset{x \to x_0^{-}}{lim} \ f(x)=\infty $，或 $\underset{x \to x_0^{+}}{lim} \  f(x)=\infty $，则 $x={{x}_{0}}$ 称为 $y=f(x)$ 的铅直渐近线。

　　(3) 斜渐近线 若  $a=\underset{x \to \infty }{lim}  \ \frac{f(x)}{x},\quad b=\underset{x \to \infty }{lim}  \ [f(x)-ax]$，则 $y=ax+b$ 称为 $y=f(x)$ 的斜渐近线。

14 函数凹凸性的判断

　　Th1: (凹凸性的判别定理）若在 $I$ 上$f''(x)<0$（或$f''(x)>0$），则 $f(x)$ 在 $I$ 上是凸的（或凹的）。

　　Th2: (拐点的判别定理 1) 若在 ${x_0}$ 处 $f''(x)=0$，（或 $f''(x)$ 不存在），当 $x$ 变动经过 ${x_0}$ 时，$f''(x)$ 变号，则 $({x_0},f({x_0}))$ 为拐点。

　　Th3: (拐点的判别定理 2) 设 $f(x)$ 在 ${x_0}$ 点的某邻域内有三阶导数，且 $f''(x)=0$，$f'''(x)\ne 0$，则 $({x_0},f({{x}_{0}}))$ 为拐点。

15 弧微分

　　$dS=\sqrt{1+y{{'}^{2}}}dx$