机器学习——极大似然估计

1 前言

• 极大似然估计方法(Maximum Likelihood Estimate，MLE)也称为最大概似估计或最大似然估计，是求估计的另一种方法，极大似然估计是1821年首先由德国数学家高斯(C. F. Gauss)提出，但是这个方法通常被归功于英国的统计学家。罗纳德·费希尔(R. A. Fisher)。
• 极大似然估计，通俗来说，就是利用已知的样本结果信息，反推最具有可能(最大概率)导致这些样本结果出现的模型参数值！
• 换句话说，极大似然估计提供了一种给定观察数据来评估模型参数的方法，即：“模型已定，参数未知”。假设我们要统计全国人口的身高，首先假设这个身高服从服从正态分布，但是该分布的均值与方差未知。我们没有人力与物力去统计全国每个人的身高，但是可以通过采样，获取部分人的身高，然后通过最大似然估计来获取上述假设中的正态分布的均值与方差。
• 最大似然估计中采样需满足一个很重要的假设，就是所有的采样都是独立同分布的。

2 求解步骤及例子

2.1 一般步骤　　

　　求极大似然函数估计值的一般步骤：

1. 写出似然函数；
2. 对似然函数取对数，并整理；
3. 求导数 ；
4. 解似然方程 。

　　以下极大似然估计法的具体做法：

　　根据总体的分布，建立似然函数$L(x_1,x_2,...,x_n;\theta_1,\theta_2 ,...,\theta_n)$ ;
　　当 $L$ 关于 可微时，(由微积分求极值的原理）可由方程组
　　　　$\frac{\partial L}{\partial \theta_i } =0,i=1,2,...,k$
　　定出 $\widehat{\theta } _i(i=1,2,...,k)$，称以上方程组为似然方程。
　　因为 $L$ 与$ln \  L$有相同的极大值点，所以 $\widehat{\theta } _i(i=1,2,...,k)$ 也可以由方程组

　　　　$\frac{\partial lnL}{\partial \theta_i } =0,i=1,2,...,k$

　　定出 $\widehat{\theta } _i(i=1,2,...,k)$，称以上方程组为对数似然方程；$\widehat{\theta } _i(i=1,2,...,k)$ 就是所求参数 $\theta _i(i=1,2,...,k)$ 的极大似然估计量。

2.2 离散型极大似然估计求解

• 若总体 $X$ 为离散型，其概率分布列为 $P(X=x)=p(x;\theta )$ ，其中 $\theta$ 为未知参数。
• 设 $(X_1,X_2,...,X_n)$ 是取自总体的样本容量为 $n$ 的样本，则 $(X_1,X_2,...,X_n)$ 的联合分布律为 $\prod \limits _{i=1}^{n}p(x_i,\theta ) $ 。
• 设 $(X_1,X_2,...,X_n)$ 的一组观测值为 $(x_1,x_2,...,x_n)$ 。
• 易知样本 $X_1,X_2,...,X_n$ 取到观测值 $x_1,x_2,...,x_n$ 的概率为

　　　　$L(\theta )=L(x_1,x_2,...,x_n;\theta )=\prod \limits _{i=1}^{n}p(x_i;\theta ) $

　　 这一概率随 $\theta$ 的取值而变化，它是 $\theta$ 的函数，称 $L(\theta )$ 为样本的似然函数。

• 极大似然估计法原理就是固定样本观测值 $(x_1,x_2,...,x_n)$ ，挑选参数 $\theta$ 使

　　　　 $L(x_1,x_2,...,x_n; \widehat{\theta} )=max \ L(x_1,x_2,...,x_n;\theta)$

• 得到的 $ \widehat{\theta} $ 与样本值有关，$\widehat{\theta } (x_1,x_2,...,x_n)$ 称为参数 $\theta$ 的极大似然估计值，其相应的统计量 $\widehat{\theta }(X_1,X_2,...,X_n)$ 称为 $\theta$ 的极大似然估计量。极大似然估计简记为 MLE 或 $\widehat{\theta }$ 。

• 问题是如何把参数 $\theta$ 的极大似然估计 $\widehat{\theta }$ 求出。更多是利用 $lnL(\theta)$是$ln(\theta)$ 的增函数，故 $lnL(\theta)$ 与 $L(\theta)$ 在同一点处达到最大值，于是对似然函数 $L(\theta)$ 取对数，利用微分学知识转化为求解对数似然方程

　　　　$\frac{\partial \  ln \ L(\theta )}{\partial \theta_i} =0,\ j=1,2...,k$

• 解此方程并对解做进一步的判断。但由最值原理，如果最值存在，此方程组求得的驻点即为所求的最值点，就可以很到参数的极大似然估计。极大似然估计法一般属于这种情况，所以可以直接按上述步骤求极大似然估计。

　　总结起来，最大似然估计的目的就是：利用已知的样本结果，反推最有可能（最大概率）导致这样结果的参数值。

　　例1：有两外形相同的箱子，各装100个球，一箱99个白球1个红球，一箱1个白球99个红球，现从两箱中任取一箱，并从箱中任取一球，问：所取的球来自哪一箱 ?  答：第一箱。

　　　　

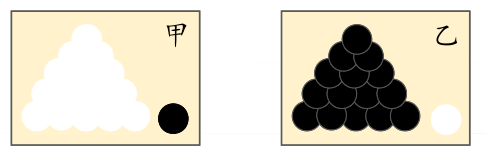
　　由于样本集中的样本都是独立同分布，可以只考虑一类样本集 D，来估计参数向量 θ。记已知的样本集为：

　　　　$D=\left\{x_{1}, x_{2}, \cdots, x_{N}\right\}$

 　　似然函数（linkehood function）：联合概率密度函数 $p(D \mid \theta)$ 称为相对于 $\left\{x_{1}, x_{2}, \cdots, x_{N}\right\}$ 的 θ 的似然函数。

　　　　$l(\theta)=p(D \mid \theta)=p\left(x_{1}, x_{2}, \cdots, x_{N} \mid \theta\right)=\prod \limits _{i=1}^{N} p\left(x_{i} \mid \theta\right)$

　　如果  $\hat{\theta}$  是参数空间中能使似然函数  $l(\theta)$ 最大的  $\theta$ 值，则  $\hat{\theta}$   应该是“最可能"的参数值， 那么  $\hat{\theta}$  就是  $\theta$  的极大似然估计 量。它是样本集的函数，记作:

　　　　$\hat{\theta}=d\left(x_{1}, x_{2}, \cdots, x_{N}\right)=d(D)$

　　　　$\hat{\theta}\left(x_{1}, x_{2}, \cdots, x_{N}\right) $  称作极大似然函数估计值 

　　求解极大似然函数

　　ML估计：求使得出现该组样本的概率最大的 θ 值。

 　　　　$\hat{\theta}= \underset{\theta}{arg \  max}  \   l(\theta)=\underset{\theta}{arg \  max}\prod \limits _{i=1}^{N} p\left(x_{i} \mid \theta\right)$

　　实际中为了便于分析，定义了对数似然函数：

　　　　$H(\theta)=\ln l(\theta)$

　　　　$\hat{\theta}= \underset{\theta}{arg \  max} \  H(\theta)= \underset{\theta}{arg \  max} \  \ln l(\theta)= \underset{\theta}{arg \  max} \  \sum \limits _{i=1}^{N} \ln p\left(x_{i} \mid \theta\right)$

　　例2：设 $X\sim b(1, p)$ 即 $(0-1)$ 分布； $X_1,X_2,...,X_n$ 是来自 $X$ 的一个样本，求参数 $P$ 的最大似然估计值。

　　解：设 $x_1,x_2,...,x_n$  是一个样本值，$X$ 的分布律为

　　　　$P\{X=x \}=p^x(1-p)^{1-x},\quad x=0,1$

　　得出似然函数为

　　　　$L(p)=\prod \limits _{i=1}^{n}p^{x_i} (1-p)^{1-x_i} =p^{\ \sum \limits _{i=1}^{n}x_i }  (1-p)^{\ n-\sum \limits _{i=1}^{n}x_i }$

　　对似然函数取 $ln$ 对数得

　　　　$ln \ L(p)=(\sum \limits _{i=1}^{n}{x_i})ln\ p+(n-\sum \limits _{i=1}^{n}x_i )ln\ (1-p)$

　　使$ln \  L(p)$对概率求导得

　　　　$\frac{d}{dp} ln \ L(p)=\frac{1}{p}\sum\limits _{i=1}^{n} x_i-\frac{1}{1-p}(n-\sum\limits _{i=1}^{n}x_i)$

　　令导数等于 $0$得

　　　　$\frac{d}{dp} ln \ L(p)=0$

　　解得 $p$ 的最大似然估计值

　　　　$\widehat{p}=\frac{1}{n} \sum \limits _{i=1}^{n}x_i=\bar{x} $

　　则 $p$ 的最大似然估计量为

　　　　$\widehat{p}=\frac{1}{n} \sum \limits _{i=1}^{n}X_i=\bar{X} $

　　它与矩估计量是相同的。

2.3 连续型极大似然估计求解

• 若总体 $X$ 为连续型，其概率密度函数为 $f(x;\theta )$，其中 $\theta $ 为未知参数。
• 设 $(X_1,X_2,...,X_n)$ 是取自总体的样本容量为 $n$ 的简单样本，则 $(X_1,X_2,...,X_n)$ 的联合概率密度函数为 $\prod \limits _{i=1}^{n}f(x_i;\theta )$ 。
• 设 $(X_1,X_2,...,X_n)$ 的一组观测值为 $(x_1,x_2,...,x_n)$ ，则随机点 $(X_1,X_2,...,X_n)$ 落在点 $(x_1,x_2,...,x_n)$ 的邻边（边长分别为 $dx_1,dx_2,...,dx_n$ 的 $n$ 维立方体）内的概率近似地为 $\prod \limits _{i=1}^{n}f(x_i;\theta )dx_i$。
• 考虑函数

　　　　 $L(\theta )=L(x_1,x_2,...,x_n;\theta )=\prod \limits _{i=1}^{n}f(x_i;\theta )$
　　   同样， $L(\theta )$ 称为样本的似然函数。

• 得到的 $ \widehat{\theta} $ 与样本值有关，$\widehat{\theta } (x_1,x_2,...,x_n)$ 称为参数 $\theta$ 的极大似然估计值，其相应的统计量 $\widehat{\theta }(X_1,X_2,...,X_n)$ 称为 $\theta$ 的极大似然估计量。极大似然估计简记为 MLE 或 $\widehat{\theta }$ 。
• 问题是如何把参数 $\theta$ 的极大似然估计 $\widehat{\theta }$ 求出。更多是利用 $lnL(\theta)$ 是 $ln(\theta)$ 的增函数，故 $lnL(\theta)$ 与 $L(\theta)$ 在同一点处达到最大值，于是对似然函数 $L(\theta)$ 取对数，利用微分学知识转化为求解对数似然方程

　　　　$\frac{\partial \  ln \ L(\theta )}{\partial \theta_i} =0,\ j=1,2...,k$

• 解此方程并对解做进一步的判断。但由最值原理，如果最值存在，此方程组求得的驻点即为所求的最值点，就可以很到参数的极大似然估计。极大似然估计法一般属于这种情况，所以可以直接按上述步骤求极大似然估计。　

　　例：设 $X\sim N(\mu,\sigma ^2)$ ；$\mu，\sigma ^2$ 为未知参数，$x_1,x_2,...,x_n$ 是来自 $X$ 的一个样本值，求： $\mu,\sigma ^2$ 的最大似然估计。
　　解：$X$ 的概率密度为:

　　　　$f(x;\mu,\sigma ^2)=\frac{1}{\sqrt{2\pi } \sigma } e^{-\frac{1}{2\sigma ^2}(x-\mu)^2 }$

　　联合概率密度为

　　　　$p(x_1,x_2,...,x_n)=\prod \limits _{i=1}^{n} \frac{1}{\sqrt{2\pi } \sigma } e^{-\frac{1}{2\sigma ^2}(x_i-\mu)^2 }$

　　于是得似然函数为

　　　　$L(\mu,\sigma ^2)=\prod \limits _{i=1}^{n} \frac{1}{\sqrt{2\pi } \sigma } e^{-\frac{1}{2\sigma ^2}(x_i-\mu)^2 }$

　　似然函数取对数

　　　　$ln \ L=-\frac{n}{2}ln\ (2\pi)- \frac{n}{2}ln\ (\sigma ^2)-\frac{1}{2\sigma ^2} \sum \limits _{i=1}^{n}(x_i-\mu)^2 $

　　似然方程组为：

　　　　$\frac{\partial }{\partial x} ln \ L=\frac{1}{\sigma ^2} \sum \limits _{i=1}^{n} (x_i-\mu)=0$
　　　　$\frac{\partial }{\partial \sigma ^2} ln \ L = \frac{1}{2(\sigma ^2)^2} \sum \limits _{i=1}^{n} (x_i-\mu)-\frac{n}{2(\sigma ^2)} =0$

　　得出：

　　　　$\widehat{\mu}_{mle}=\frac{1}{n} \sum \limits _{i=1}^{n}x_i=\bar{x} $
　　　　$\widehat{\sigma ^2}_{mle}=\frac{1}{n} \sum \limits _{i=1}^{n}(x_i-\bar{x} )^2$

　　故 $\mu ,\sigma ^2$ 的极大似然估计量分别为

　　　　$\frac{1}{n}\sum_\limits {i=1}^{n}X_i=\bar{X} ,\frac{1}{n}\sum_\limits {i=1}^{n}(X_i-\bar{X} )^2=S_{n}^{2}$