机器学习——梯度下降法

1 前言

　　机器学习和深度学习里面都至关重要的一个环节就是优化损失函数，一个模型只有损失函数收敛到一定的值，才有可能会有好的结果，降低损失的工作就是优化方法需做的事。常用的优化方法：梯度下降法家族、牛顿法、拟牛顿法、共轭梯度法、Momentum、Nesterov Momentum、Adagrad、RMSprop、Adam等。
　　梯度下降法不论是在线性回归还是 Logistic 回归中，主要目的是通过迭代找到目标函数的最小值，或者收敛到最小值。
　　梯度下降法作为机器学习中较常使用的优化算法，其有着三种不同的形式：

1. 批量梯度下降（Batch Gradient Descent）
2. 随机梯度下降（Stochastic Gradient Descent）
3. 小批量梯度下降（Mini-Batch Gradient Descent）

　　其中小批量梯度下降法也常用在深度学习中进行模型的训练。接下来，将逐步对这三种不同的梯度下降法进行理解。

　　为方便理解这三种梯度下降法，可以参考本博客《机器学习——批量梯度下降法、随机梯度下降法、小批量梯度下降法》

2 梯度下降算法

2.1 场景假设

　　梯度下降法的基本思想可以类比为一个下山的过程。
　　假设这样一个场景：一个人被困在山上，需要从山上找到山的最低点。但此时山上的浓雾很大，导致可视度很低；因此，下山的路径就无法确定，必须利用自己周围的信息一步一步地找到下山的路。这个时候，便可利用梯度下降算法来帮助自己下山。
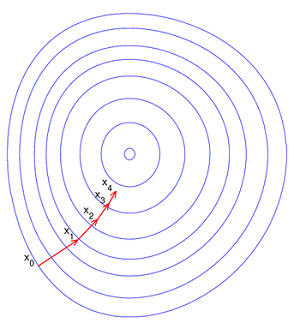
　　怎么做呢？首先以他当前的所处的位置为基准，寻找这个位置最陡峭的地方，然后朝着下降方向走一步，然后又继续以当前位置为基准，再找最陡峭的地方，再走直到最后到达最低处。

　　

2.2 梯度下降

　　梯度下降的基本过程就和下山的场景很类似。
　　首先，我们有一个可微分的函数，代表着一座山。目标是找到这个函数的最小值，也就是山底。
　　根据之前的场景假设，最快的下山的方式就是找到当前位置最陡峭的方向，然后沿着此方向向下走。对应到函数中，就是找到给定点的梯度 ，然后朝着梯度相反的方向，就能让函数值下降的最快！
　　重复利用这个方法，反复求取梯度，最后就能到达局部的最小值，这就类似于我们下山的过程。而求取梯度就确定了最陡峭的方向，也就是场景中测量方向的手段。

2.2.1 微分

　　微分例子：
　　1.单变量的微分，函数只有一个变量时
　　　　${\large \frac{\mathrm{d}(x^{2}) }{\mathrm{d} x} =2x} $
　　2.多变量的微分，当函数有多个变量的时候，分别对每个变量进行求微分
　　　　${\large \frac{\partial (x^{2}y^{2})}{\partial x} =2xy^{2}} $

2.2.2 梯度

　　梯度实际上就是多变量微分的一般化。
　　例子：
　　　　$J(\theta )=5-(4\theta_{1} +3\theta_{2}-2\theta_{3})$
　　　　$\nabla J(\Theta)=\left\langle\frac{\partial J}{\partial \theta_{1}}, \frac{\partial J}{\partial \theta_{2}}, \frac{\partial J}{\partial \theta_{3}}\right\rangle=(-5,-2,12)$
　　可以看到，梯度就是分别对每个变量进行微分，然后用逗号分割开，梯度是用$<>$包括起来，说明梯度其实一个向量。

1. 在单变量的函数中，梯度其实就是函数的微分，代表着函数在某个给定点的切线的斜率。
2. 在多变量函数中，梯度是一个向量，向量有方向，梯度的方向就指出了函数在给定点的上升最快的方向。梯度的方向是函数在给定点上升最快的方向，那么梯度的反方向就是函数在给定点下降最快的方向。

2.2.3 数学解释

　　数学公式：$\theta ^{1} =\theta ^{0} +\alpha \bigtriangledown J(\theta)$
　　意义是：$J$  是关于 $\theta$ 的一个函数，当前所处位置为 $\theta ^{0}$ 点，要从这个点走到 $J$ 的最小值点。首先先确定前进的方向：梯度的反向。然后走一段距离的步长： $\alpha$ ，走完这个段步长，到达 $\theta ^{1}$！

2.2.4 学习率 α

　　$\alpha$ 在梯度下降算法中被称为 学习率 或者 步长。通过 $\alpha$ 来控制每一步距离，以保证步子不要跨太大，避免走太快，错过最低点。同时也要保证不要走的太慢，影响效率。$\alpha$ 不能太大也不能太小，太小的话，可能导致走不到最低点；太大的话，导致错过最低点。

2.2.5 梯度乘负号

　　梯度前加负号，意味着朝梯度相反方向前进。梯度的方向就是函数在此点上升最快的方向。梯度下降需要朝下降最快的方向前进，自然是负梯度的方向，所以需要加上负号。

3 实例

3.1 单变量函数的梯度下降

　　假设有一个单变量函数：$J(\theta) =\theta ^{2} $
　　函数的微分：$J^{'} (\theta) =2\theta$
　　初始化：设置初始位置  $ \theta^{0}=1$，设置学习率： $\alpha =0.4$
　　根据梯度下降的计算公式：$\theta ^{1} =\theta ^{0} +\alpha \bigtriangledown J(\theta)$
　　计算过程：
　　　　$\theta ^{0} =1$
　　　　$\theta ^{1} =\theta ^{0}-\alpha J ^{'}(\theta ^{0})=1-0.4*2=0.2$
　　　　$\theta ^{2} =\theta ^{1}-\alpha J ^{'}(\theta ^{1})=0.2-0.4*0.4=0.04$
　　　　$\theta ^{3} =0.08$
　　　　$\theta ^{4} =0.0016$
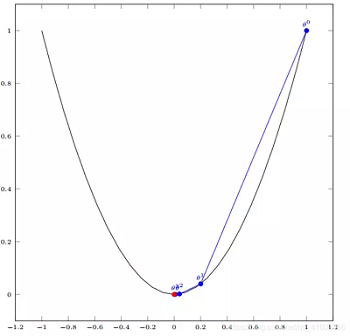
　　如图，经过四次的运算，也就是走了四步，基本抵达函数最低点，也就是山底。

　　

3.2 多变量函数的梯度下降

　　假设有一个目标函数：$J(\theta)=\theta_{1}^{2} +\theta_{2}^{2}$
　　假设初始起点：$\theta^{0}= (1,3)$，初始学习率：$\alpha =0.1$
　　函数的梯度为：$\bigtriangledown J(\theta)=<2\theta_{1},2\theta_{2}>$
　　计算过程：
　　　　$\begin{array}{l} \Theta^{0}=(1,3) \\ \Theta^{1}=\Theta^{0}-\alpha \nabla J(\Theta)=(1,3)-0.1 *(2,6)=(0.8,2.4) \\ \Theta^{2}=(0.8,2.4)-0.1 *(1.6,4.8)=(0.64,1.92) \\ \Theta^{3}=(0.5124,1.536) \\ \Theta^{4}=(0.4096,1.228800000000001) \\ \vdots \\ \Theta^{10}=(0.1073741824000003,0.32212254720000005) \\ \Theta^{50}=\left(1.141798154164342 e^{-05}, 3.42539442494306 e^{-05}\right) \\ \vdots \\ \Theta^{100}=\left(1.6296287810675902 e^{-10}, 4.8888886343202771 e^{-10}\right) \end{array}$
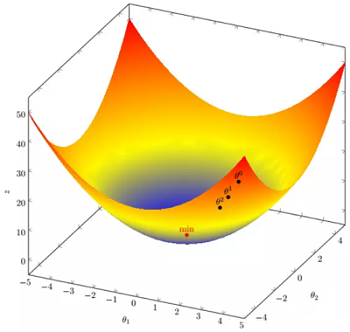
　　我们发现，已经基本靠近函数的最小值点：

　　

4 批量梯度下降

　　为了便于理解，这里使用只含有一个特征的线性回归来展开。
　　此时线性回归的假设函数为：

　　　　$h_{\theta} (x^{(i)})=\theta_1 x^{(i)}+\theta_0$

　　其中 $i=1,2,...,m$，其中 $m$ 表示样本数。
　　对应的目标函数（代价函数）即为：

　　　　$J(\theta_0, \theta_1) = \frac{1}{2m} \sum_ \limits {i=1}^{m}(h_{\theta}(x^{(i)}) - y^{(i)})^2$

　　批量梯度下降法是最原始的形式，它是指在每一次迭代时使用所有样本来进行梯度的更新。从数学上理解如下：
　　(1)对目标函数求偏导

　　　　$\frac{\Delta J(\theta_0,\theta_1)}{\Delta \theta_j} = \frac{1}{m} \sum_ \limits {i=1}^{m} (h_{\theta}(x^{(i)})-y^{(i)})x_j^{(i)}$

　　其中 $i=1,2,...,m$，$m$ 表示样本数，$j = 0,1$ 表示特征数，这里我们使用了偏置项 $x_0^{(i)} = 1$
　　(2)每次迭代对参数进行更新：

　　　　$\theta_j := \theta_j - \alpha \frac{1}{m} \sum_ \limits {i=1}^{m} (h_{\theta}(x^{(i)})-y^{(i)})x_j^{(i)}$

　　注意：这里更新时存在一个求和函数，即为对所有样本进行计算处理，可与下文SGD法进行比较。
　　优点：
  (1)一次迭代是对所有样本进行计算，此时利用矩阵进行操作，实现了并行。
  (2)由全数据集确定的方向能够更好地代表样本总体，从而更准确地朝向极值所在的方向。当目标函数为凸函数时，BGD一定能够得到全局最优。
  缺点：
  (1)当样本数目 $m$ 很大时，每迭代一步都需要对所有样本计算，训练过程会很慢。
  从迭代的次数上来看，BGD迭代的次数相对较少。

5 随机梯度下降

随机梯度下降法不同于批量梯度下降，随机梯度下降是每次迭代使用一个样本来对参数进行更新。使得训练速度加快。
  对于一个样本的目标函数为：

　　　　$J^{(i)}(\theta_0,\theta_1) = \frac{1}{2}(h_{\theta}(x^{(i)})-y^{(i)})^2$

　　(1)对目标函数求偏导：

　　　　$\frac{\Delta J^{(i)}(\theta_0,\theta_1)}{\theta_j} = (h_{\theta}(x^{(i)})-y^{(i)})x^{(i)}_j$

　　(2)参数更新：

　　　　$\theta_j := \theta_j - \alpha  (h_{\theta}(x^{(i)})-y^{(i)})x^{(i)}_j$

　　注意：这里不再有求和符号

6 小批量梯度下降

　　小批量梯度下降，是对批量梯度下降以及随机梯度下降的一个折中办法。其思想是：每次迭代 使用  batch_size 个样本来对参数进行更新。
  这里我们假设$batch_size = 10$，样本数$m=1000$

 　　优点：
  （1）通过矩阵运算，每次在一个 batch 上优化神经网络参数并不会比单个数据慢太多。
  （2）每次使用一个 batch 可以大大减小收敛所需要的迭代次数，同时可以使收敛到的结果更加接近梯度下降的效果。(比如上例中的30W，设置 batch_size=100 时，需要迭代 3000 次，远小于 SGD 的 30W 次)
  （3）可实现并行化。
  缺点：
  （1）batch_size的不当选择可能会带来一些问题。
  batcha_size的选择带来的影响：
  （1）在合理地范围内，增大batch_size的好处：
    a. 内存利用率提高了，大矩阵乘法的并行化效率提高。
    b. 跑完一次 epoch（全数据集）所需的迭代次数减少，对于相同数据量的处理速度进一步加快。
    c. 在一定范围内，一般来说 Batch_Size 越大，其确定的下降方向越准，引起训练震荡越小。
  （2）盲目增大batch_size的坏处：
    a. 内存利用率提高了，但是内存容量可能撑不住了。
    b. 跑完一次 epoch（全数据集）所需的迭代次数减少，要想达到相同的精度，其所花费的时间大大增加了，从而对参数的修正也就显得更加缓慢。
    c. Batch_Size 增大到一定程度，其确定的下降方向已经基本不再变化。

参考文献：

批量梯度下降(BGD)、随机梯度下降(SGD)以及小批量梯度下降(MBGD)的理解

梯度下降算法原理讲解——机器学习