机器学习——信息论基础
1 前言
机器学习中，绕不开的一个概念就是熵 (Entropy)，信息熵。信息熵常被用来作为一个系统的信息含量的量化指标，用来作为系统方程优化的目标或者参数选择的判据。
2 熵的定义？
信息熵的定义公式：
$H(X)=-\sum \limits_{x\in \mathrm{x}}p(x)\ log p(x)$
并且规定 0log(0) = 0
熵度量了事物的不确定性，越不确定的事物，它的熵就越大。在没有外部环境的作用下，事物总是向着熵增大的方向发展，所以熵越大，可能性也越大。
2.1 信息熵的三个性质
信息论背后的思想：一件不太可能的事件比一件比较可能的事件更有信息量。
信息(Information)需要满足的三个条件：
单调性：比较可能发生的事件的信息量要少；
非负性：信息熵可以看作为一种广度量，非负性是一种合理的必然；
累加性：独立发生的事件之间的信息量应该是可以叠加的。例如，投掷的硬币两次正面朝上传递的信息量，应该是投掷一次硬币正面朝上的信息量的两倍。
香农从数学上严格证明了满足上述三个条件的随机变量不确定性度量函数具有唯一形式
$H(X)=-C\sum_ \limits{x\in \mathrm{x}}p(x)log p(x)$
其中的 C 为常数，我们将其归一化为C=1 即得到了信息熵公式。
2.2 对信息熵三条性质的理解
单调性：事件发生概率越低，发生时所能给出的信息量越大。
举一个极端的例子，“太阳从西边升起”所携带的信息量就远大于“太阳从东边升起”。后者是一个万年不变的事实，而前者是一个相当不可能发生的事情。如果发生了，那代表了太多的可能性，可能太阳系有重大变故，可能物理法则发生了变化等。从某种角度来考虑，单调性也暗含了一种对信息含量的先验假设，即默认某些事实是不含信息量的（默认事实其实也是一种信息），这其实是把默认情况的信息量定标为 0了。
对累加性的解释，考虑到信息熵的定义涉及到了事件发生的概率，可以假设信息熵是事件发生概率的函数：
$H(X)=H(p(x))$
对于两个相互独立的事件 X = A , Y = B 来说，其同时发生的概率：
$p(X=A,Y=B)=p(X=A) \cdot p(X=B)$
其同时发生的信息熵，根据累加性可知：
$H(p(X=A,Y=B))=H(p(X=A)\cdotp(X=B) )=H(p(X=A))+H(p(Y=B))$
函数形式，满足两个变量乘积函数值等于两个变量函数值的和，那么这种函数形式应该是对数函数。再考虑到概率都是小于等于1 的，取对数之后小于0，考虑到信息熵的第二条性质，所以需要在前边加上负号。
2.3 自信息
自信息（英语：self-information），又译为信息本体，由克劳德·香农提出，用来衡量单一事件发生时所包含的信息量多寡。它的单位是bit,或是nats。
自信息的含义包括两个方面：
1.自信息表示事件发生前，事件发生的不确定性。
2.自信息表示事件发生后，事件所包含的信息量，是提供给信宿的信息量，也是解除这种不确定性所需要的信息量。
对事件$\mathrm{x}=x $，我们定义：
$I(x)=-logP(x)$
自信息满足上面三个条件，单位是奈特(nats)（底为e）。
3 伯努利分布熵的计算
熵的定义公式中对数函数不局限于采用特定的底，不同的底对应了熵的不同度量单位。如以2 为底，熵的单位称作比特 (bit)，如以自然对数 e 为底，熵的单位称作纳特 (nat)。从熵的定义中可以看出，熵是关于变量 X 概率分布的函数，而与 X 的取值没有关系，所以也可将 X 的熵记作 H(p) ，熵越大代表随机变量的不确定性越大，当变量可取值的种类一定时，其取每种值的概率分布越平均，其熵值越大。熵的取值范围为：
$0\leq H(p)\leq log(n)$ n 表示取值的种类。
作为一个具体的例子，当随机变量只取两个值，例如 1，0时，即 X 的分布为：
$P(X=1)=p,P(X=0)=1-p,0\leq p\leq 1$
熵为：
$H(p)=-plog_{2}p-(1-p)log_{2}(1-p)$
熵 H(P) 随概率 p 变化的曲线如下图所示（单位为比特），
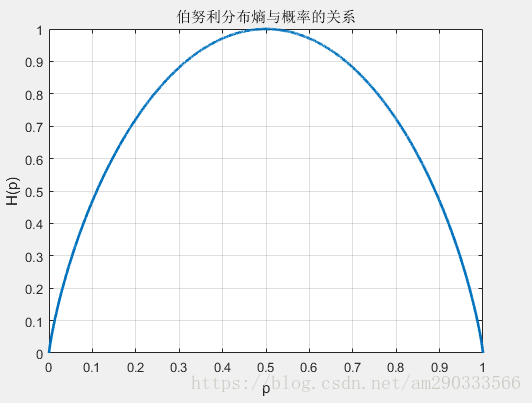
当 p=0 或 p=1 时，H(p)=0，随机变量完全没有不确定性。当 p=0.5 时， H(p)=1， 熵取值最大，随机变量不确定性最大。
4 两随机变量系统中熵的相关概念
以上介绍了关于单随机变量系统的熵的计算，现实中的系统很多是含有多随机变量的。为简化问题，以两随机变量系统来说，介绍几个与熵相关的概念。
4.1 互信息
互信息(Mutual Information)是信息论里一种有用的信息度量，它可以看成是一个随机变量中包含的关于另一个随机变量的信息量，或者说是一个随机变量由于已知另一个随机变量而减少的不肯定性 。
表示两个事件的信息相交的部分。
两个离散随机变量 X 和 Y 的互信息 (Mutual Information) 定义为：
$I(X,Y)=\sum \limits_{y\in Y}\sum \limits_{x\in X}p(x,y)log\frac{p(x,y)}{p(x)p(y)}$
连续型随机变量X 和 Y 的互信息 (Mutual Information) 定义为：
$I(X,Y)=∫_X∫_YP(X,Y)log\frac{P(X,Y)}{P(X)P(Y)}$
$I(X,Y)=H(Y)-H(Y|X)$
$I(X,Y)=H(Y)+H(X)-H(X,Y)$
其中H(X)和H(Y) 是边缘熵，H(X|Y)和H(Y|X)是条件熵，而H(X,Y)是X和Y的联合熵。注意到这组关系和并集、差集和交集的关系类似，用Venn图表示：
可以看出，I(X,Y)可以解释为由X引入而使Y的不确定度减小的量，这个减小的量为H(Y|X)。所以，如果X,Y关系越密切，I(X,Y)就越大，X,Y完全不相关，I(X,Y)为0，所以互信息越大，代表这个特征的分类效果越好。
为了理解互信息的涵义，我们把公式中的对数项分解
$log\frac{p(X,Y)}{p(X)p(Y)}=log(p(x,y)−(logp(x)+logp(y))=-logp(x)-logp(y)-(-logp(x,y))$
我们知道概率取负对数表征了当前概率发生所代表的信息量。上式表明，两事件的互信息为各自事件单独发生所代表的信息量之和减去两事件同时发生所代表的信息量之后剩余的信息量，这表明了两事件单独发生给出的信息量之和是有重复的，互信息度量了这种重复的信息量大小。最后再求概率和表示了两事件互信息量的期望。
从式中也可以看出，当两事件完全独立时，$p(x,y)=p(x)\cdot p(y)$，互信息计算为0，这也是与常识判断相吻合的。
4.2 联合熵
两个离散随机变量 X 和 Y 的联合熵 (Joint Entropy) 为：
$H(X,Y)=-\sum \limits_{y\in Y}\sum \limits_{x\in X}p(x,y)logp(x,y)$
联合熵表征了两事件同时发生系统的不确定度。
4.3 条件熵
表示某件事情已经发生的情况下，另外一件事情的熵。
条件熵 (Conditional Entropy)H(Y∣X) 表示在已知随机变量 X 的条件下随机变量 Y 的不确定性。
$H(Y|X)=H(X,Y)-H(X)=-\sum \limits_{y\in Y}\sum \limits_{x\in X}p(x,y)logp(y|x)$
4.4 相对熵
相对熵 (Relative Entropy) 也称 KL 散度，设 p(x)、 q(x) 是离散随机变量 X 的两个概率分布，则 p 对 q 的相对熵为：
$D_{KL}(p||q)=\sum \limits_{x}p(x)logp\frac{p(x)}{q(x)} =E_{p(x)} log(\frac{p(x)}{q(x)})$
4.5 交叉熵
考虑一种情况，对于一个样本集，存在两个概率分布 p(x) 和 q(x)，其中 p(x) 为真实分布，q(x) 为非真实分布。基于真实分布p(x) 我们可以计算这个样本集的信息熵也就是编码长度的期望为：
$H(p)=-\sum \limits_{x}p(x)logp(x)$
回顾一下负对数项表征了所含的信息量，如果我们用非真实分布 q(x) 来代表样本集的信息量的话，那么：
$H(p,q)=-\sum \limits_{x}p(x)logq(x)$
因为其中表示信息量的项来自于非真实分布q(x)，而对其期望值的计算采用的是真实分布 p(x)，所以称其为交叉熵 (Cross Entropy)。
4.6 信息变差
信息变差(Variation of Information)：表示两个事件的信息不相交的部分。
$V(X,Y)=H(X,Y)-I(X,Y)$
5. 小结
- 信息熵是衡量随机变量分布的混乱程度，是随机分布各事件发生的信息量的期望值，随机变量的取值个数越多，状态数也就越多，信息熵就越大，混乱程度就越大。当随机分布为均匀分布时，熵最大；信息熵推广到多维领域，则可得到联合信息熵；条件熵表示的是在 X 给定条件下，Y 的条件概率分布的熵对 X的期望。
- 相对熵可以用来衡量两个概率分布之间的差异。
- 交叉熵可以来衡量在给定的真实分布下，使用非真实分布所指定的策略消除系统的不确定性所需要付出的努力的大小。
6.参考文献
因上求缘，果上努力~~~~ 作者：图神经网络，转载请注明原文链接：https://www.cnblogs.com/BlairGrowing/p/14810741.html
