深度学习——概率与信息论

1 概率

1.1 概率与随机变量

• 频率学派概率 (Frequentist Probability)：认为概率和事件发⽣的频率相关。
• 贝叶斯学派概率 (Bayesian Probability)：认为概率是对某件事发⽣的确定程度，可以理解成是确信的程度。
• 随机变量 (Random Variable)：⼀个可能随机取不同值的变量。例如：抛掷⼀枚硬币，出现正⾯或者反⾯的结果。

1.2 概率分布

1.2.1 概率质量函数

　　概率质量函数 (Probability Mass Function)：对于离散型变量，我们先定义⼀个随机变量，然后⽤ ~ 符号来说明它遵循的分布：x∼P (x) ，函数 P 是随机变量 x 的 PMF。

　　例如, 考虑⼀个离散型变量 x 有 k 个不同的值，我们可以假设 x 是均匀分布的 (也就是将它的每个值视为等可能的)，通过将它的 PMF 设为：

　　　　$P(\mathrm{x}=x_{i})=\frac{1}{k}$

　　对于所有的 i 都成⽴。

1.2.2 概率密度函数

 　　研究对象是连续型时，可以引⼊同样的概念。如果⼀个函数 p 是概率密度函数 (Probability Density Function)：

 　　• 分布满⾜⾮负性条件：$\forall x \in \mathrm{x},p(x)\geqslant 0$

 　　• 分布满⾜归⼀化条件：$\int_{-\infty}^\infty p(x)=1$

 　　例如在 (a, b) 上的均匀分布：

　　　　$U(x;a,b)=\frac{1_{ab(x)}}{b-a}$

 　　这⾥ $1_{ab(x)} $表⽰在 (a, b) 内为 1，否则为 0。

1.2.3 累积分布函数

　　累积分布函数 (Cummulative Distribution Function) 表⽰对⼩于 x 的概率的积分：

　　　　$CDF(x)=\int_{-\infty}^x p(t)dt=1$

1.3 条件概率与条件独立

　　边缘概率 (Marginal Probability)：如果我们知道了⼀组变量的联合概率分布，但想要了解其中⼀个⼦集的概率分布。这种定义在⼦集上的概率分布被称为边缘概率分布。　

　　例如，假设有离散型随机变量 $\mathrm{x}$和$\mathrm{y}$，并且我们知道$P(\mathrm{x}, \mathrm{y})$。 我们可以依据下面的求和法则来计算$P(\mathrm{x})$：
　　 　　$\forall x \in \mathrm{x}, P(\mathrm{x} = x) = \sum \limits_y P(\mathrm{x} = x, \mathrm{y} = y).$

　　对于连续型变量，我们需要用积分替代求和：

　　　　$p(x) = \int p(x, y)dy.$

　　条件概率 (Conditional Probability)：在很多情况下，我们感兴趣的是某个事件，在给定其他事件发⽣时出现的概率。这种概率叫做条件概率。我们将给定$\mathrm{x} = x,\mathrm{y} = y$发⽣的条件概率记为$P(\mathrm{y}=y | \mathrm{x}=x)$。这个条件概率可以通过下⾯的公式计算:
　　　　$P(\mathrm{y}=y | \mathrm{x}=x) = \frac{P(\mathrm{y}=y, \mathrm{x}=x)}{P(\mathrm{x}=x)} .$

　　条件概率只在$P(\mathrm{x}=x)>0$时有定义。 我们不能计算给定在永远不会发生的事件上的条件概率。

　　条件概率的链式法则 (Chain Rule of Conditional Probability)：任何多维随机变量的联合概率分布，都可以分解成只有⼀个变量的条件概率相乘的形式:

　　　　$P(\mathrm{x}^{(1)}, \ldots, \mathrm{x}^{(n)}) = P(\mathrm{x}^{(1)}) \Pi_{i=2}^n P(\mathrm{x}^{(i)} \mid \mathrm{x}^{(1)}, \ldots, \mathrm{x}^{(i-1)}) .$

　　独立性 (Independence)：两个随机变量 x 和 y，如果它们的概率分布可以表⽰成两个因⼦的乘积形式，并且⼀个因⼦只包含 x 另⼀个因⼦只包含y，我们就称这两个随机变量是相互独⽴的:
　　　　$\forall x \in \mathrm{x}, y \in \mathrm{y}, p(\mathrm{x} = x, \mathrm{y} = y) = p(\mathrm{x} = x)p(\mathrm{y} = y).$　

　　条件独立性 (Conditional Independence)：如果关于$\mathrm{x}$和$\mathrm{y}$的条件概率分布对于$z$的每一个值都可以写成乘积的形式，那么这两个随机变量 $\mathrm{x}$和$\mathrm{y}$在给定随机变量~$z$时是条件独立的：

　　　　$\forall x \in \mathrm{x}, y \in \mathrm{y}, z \in \mathrm{z}, p( \mathrm{x}=x, \mathrm{y}=y \mid \mathrm{z}=z) =p(\mathrm{x} = x \mid \mathrm{z} = z) p(\mathrm{y} = y \mid \mathrm{z} = z).$　
　　我们可以采用一种简化形式来表示独立性和条件独立性：$\mathrm{x} \bot \mathrm{y}$表示$\mathrm{x}$和$\mathrm{y}$相互独立，$\mathrm{x} \bot \mathrm{y} \mid \mathrm{z}$表示$\mathrm{x}$和$\mathrm{y}$在给定$\mathrm{z}$时条件独立。

1.4 随机变量的度量

　　期望(Expectation)：函数$f(x)$关于某分布$P(\mathrm{x})$的期望或者期望值是指，当$x$由$P$产生，$f$作用于$x$时，$f(x)$的平均值。 对于离散型随机变量，这可以通过求和得到：

　　　　$E_{\mathrm{x}\sim P }[f(x)] = \sum \limits_x P(x)f(x)$
　　对于连续型随机变量可以通过求积分得到：

　　　　$E_{\mathrm{x}\sim P }[f(x)] = \int p(x)f(x)dx.$

　　另外，期望是线性的：

　　　　$E_{\mathrm{x}}[\alpha f(x) + \beta g(x)]= \alpha E_{\mathrm{x}}[f(x)] + \beta E_{\mathrm{x}}[g(x)]$

　　方差 (Variance)：衡量的是当我们对 x 依据它的概率分布进⾏采样时，随机变量 x 的函数值会呈现多⼤的差异，描述采样得到的函数值在期望上下的波动程度：

　　　　$Var(f(x)) = E [(f(x)- E[f(x)])^2 ].$

 　　将⽅差开平⽅即为标准差 (Standard Deviation)。

　　协方差 (Covariance)：⽤于衡量两组值之间的线性相关程度：

　　　　$Cov(f(x), g(y)) = E[ ( f(x)-E[f(x)] )( g(y)-E[g(y)] )].$

　　注意，独⽴⽐零协⽅差要求更强，因为独立还排除了非线性的相关。

1.5 常用概率分布

1.5.1 伯努利分布 (两点分布)

　　伯努利分布 (Bernoulli Distribution) 是单个二值随机变量的分布，是单个二值随机变量的分布。由单个参数$\phi \in [0, 1]$控制，$\phi$给出了随机变量等于1的概率。 它具有如下的一些性质：

　　　　$P(\mathrm{x} =1) = \phi$

　　　　$P(\mathrm{x} =0) = 1-\phi$

　　　　$P(\mathrm{x} = x) = \phi^x (1-\phi)^{1-x}$

　　表⽰⼀次试验的结果要么成功要么失败。

1.5.2 范畴分布 (分类分布)

　　范畴分布 (Multinoulli Distribution) 是指在具有 k 个不同值的单个离散型随机变量上的分布:

　　　　$p(\mathrm{x}=x)\prod_{i}\o_{i}^{x^{i}}$

　　例如每次试验的结果就可以记为⼀个 k 维的向量，只有此次试验的结果对应的维度记为 1，其他记为 0。

1.5.3 高斯分布 (正态分布)

　　实数上最常用的分布就是正态分布，也称为高斯分布：

　　　　$N(x; \mu, \sigma^2) = \sqrt{\frac{1}{2\pi \sigma^2}} \exp ( -\frac{1}{2\sigma^2} (x-\mu)^2 ).$

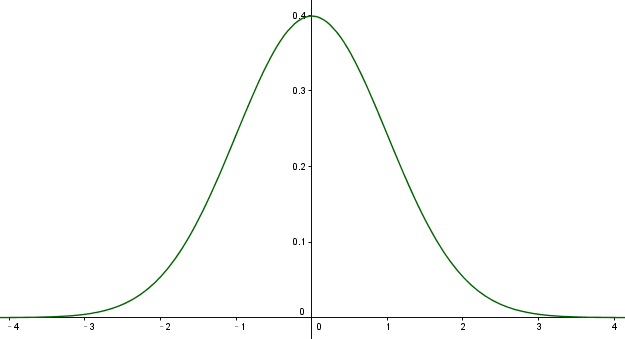
 　　正态分布由两个参数控制，$\mu \in R$和$\sigma \in (0, \infty)$。 参数$\mu$给出了中心峰值的坐标，这也是分布的均值：$E[\mathrm{x}] = \mu$。 分布的标准差用$\sigma$表示，方差用$\sigma^2$表示。

 　　 标准高斯函数

　　　　

 1.5.4 指数分布

　　在深度学习中，我们经常会需要一个在$x=0$点处取得边界点(sharp point)的分布。 为了实现这一目的，我们可以使用指数分布：

　　　　$P(x;\lambda )=\lambda 1_{x\ge 0 } exp(-\lambda x)$

　　指数分布使用指示函数(indicator function)$\Vone_{x\ge 0}$来使得当$x$取负值时的概率为零。

1.5.5 Laplace分布

　　它允许我们在任意一点$\mu$处设置概率质量的峰值

　　　　$\text{Laplace}(x; \mu, \gamma) = \frac{1}{2\gamma} \exp \left( -\frac{|x-\mu|}{\gamma} \right).$

1.5.6 Dirac分布和经验分布

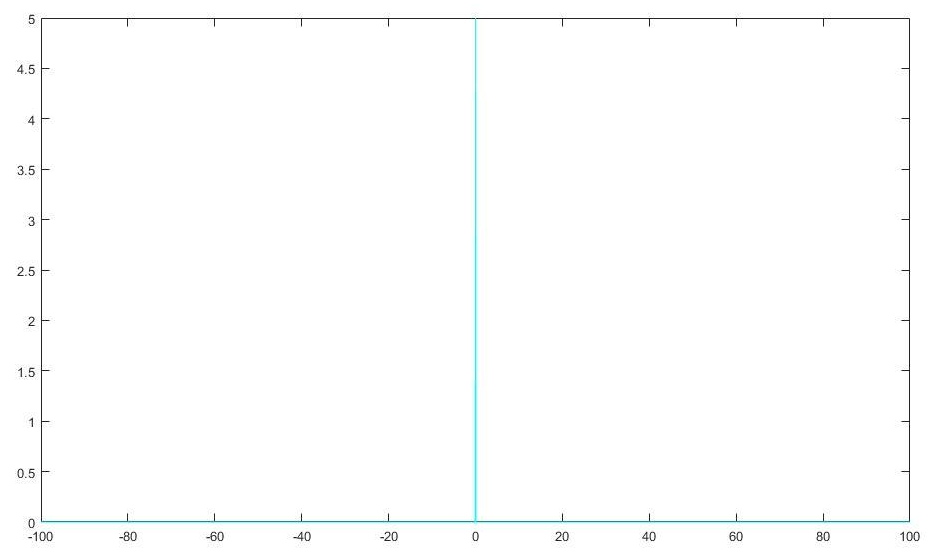
　　在一些情况下，我们希望概率分布中的所有质量都集中在一个点上。 这可以通过Dirac delta函数 $\delta(x)$定义概率密度函数来实现：

　　　　$p(x) = \delta(x-\mu).$

　　它可以描述成一个在原点处无限高，无限窄的曲线，并且它的积分为 1。也就是说只在原点处取 +∞，而在其他各处取 0。

　　　　$\delta (x)=\left\{\begin{matrix}+\infty,x=0 \\0,x=otherwise\end{matrix}\right.$

　　而其导数则为：

　　　　$\int{^{+\infty}_{-\infty}\delta(x)dx=1}$

　　图像

　　

 1.6 常用函数的有用性质

1.6.1 logistic sigmoid 函数

　　　　$\sigma (x)=\frac{1}{1+exp(-x)} $

　　　

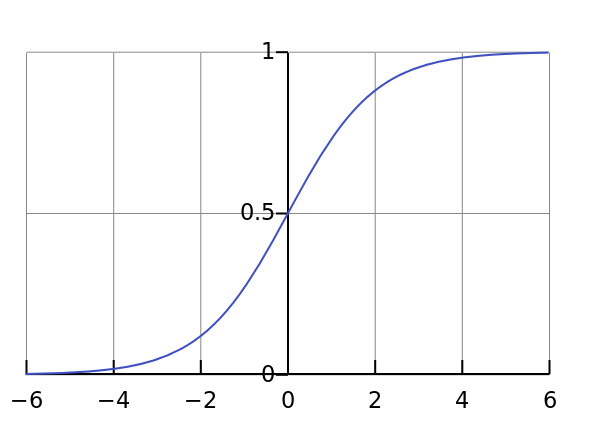
 　　logistic  sigmoid  函数通常⽤来产⽣伯努利分布中的参数 ϕ ，因为它的范围是(0, 1)，处在 ϕ 的有效取值范围内。sigmoid  函数在变量取绝对值⾮常 ⼤的正值或负值时会出现饱和  (Saturate)  现象，意味着函数会变得很平，并且对输⼊的微⼩改变会变得不敏感。

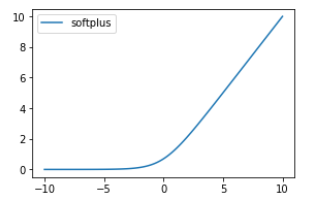
1.6.2 softplus函数

 　　$\zeta(x) = \log(1+\exp(x)).$

　　softplus函数可以用来产生正态分布的$\beta$和$\sigma$参数，因为它的范围是$(0,\infty)$。 当处理包含sigmoid函数的表达式时它也经常出现。 softplus函数名来源于它是另外一个函数的平滑（或”软化”）形式，这个函数是

　　　　$x^+ = \max(0, x).$