深度学习——正则化

1 定义

　　定义：正则化是我们对学习算法所做的任何修改，旨在减少其泛化误差( generalization error)，而不是其训练误差(training error)。
　　在深入探讨该主题之前，请查看以下图片：

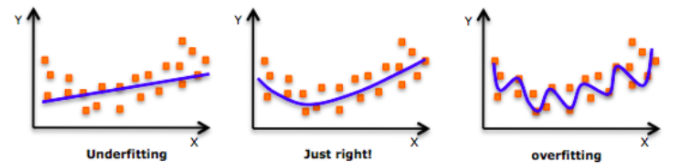
　　从左向右比较，模型不断尝试从训练数据中学习细节和噪音，慢慢很好的模拟训练数据，但最终却导致在测试数据性能不佳。换句话说，在向右移动时，模型的复杂性增加了，训练误差减少了，但测试误差却没有。如下图所示。

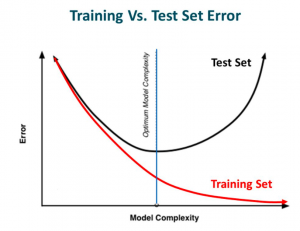
　　若博友们以前建立过神经网络，就会知道它们有多复杂，会发现网络容易出现过度拟合。

　　正则化是一种对学习算法稍加修改的技术，以使模型具有更好的泛化能力。反过来，这也提高了模型在看不见的数据上的性能。

2 正则化减少过度拟合

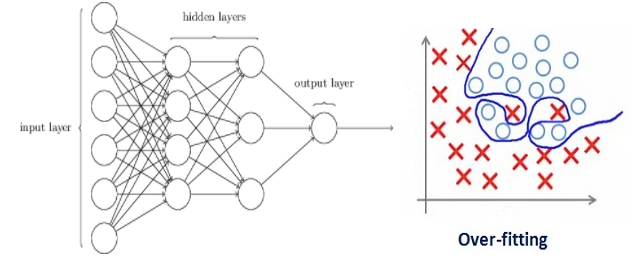
　　考虑一个神经网络，它过度拟合了训练数据，如下图所示。

　　若研究过正则化概念，将有一个公平的主意，即正则化会惩罚系数。在深度学习中，它实际上惩罚了节点的权重矩阵。
　　假设正则化系数非常高，以至于某些权重矩阵几乎等于零。

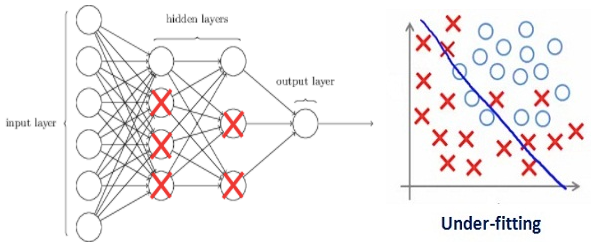
　　这将导致线性网络简单得多，并且训练数据略有不足。
　　如此大的正则化系数值没有太大用处。需要优化正则化系数的值，以便获得一个拟合良好的模型，如下图所示。

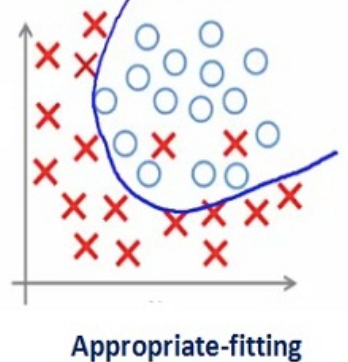
3 不同正则化技术

　　现已了解正则化如何有助于减少过拟合，本节将学习一些不同的正则化技术。
　　正则化(Regularization)是机器学习中对原始损失函数引入额外信息，以便防止过拟合和提高模型泛化性能的一类方法的统称。将目标函数变成 原始损失函数+额外项 。

　　　　Cost function = Loss (say, binary cross entropy) + Regularization term

　　常用的额外项一般有两种，英文称作 $ℓ1−norm$ 和 $ℓ2−norm$ ，中文称作 L1正则化 和 L2正则化，或 L1范数和 L2 范数(实际是L2范数的平方)。L1正则化和 L2正则化可以看做是损失函数的惩罚项。所谓惩罚是指对损失函数中的某些参数做一些限制。对于线性回归模型，使用L1正则化的模型叫做Lasso回归，使用L2正则化的模型叫做Ridge回归(岭回归)。

　　线性回归 L1 正则化损失函数：

　　　　$\min_w (\sum_{i=1}^{N}(w^Tx_i - y_i)^2 + \lambda \|w\|_1 )\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1)$

　　线性回归 L2 正则化损失函数：

　　　　$\min_w(\sum_{i=1}^{N}(w^Tx_i - y_i)^2 + \lambda\|w\|_2^2)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (2)$

　　公式(1)(2)中 $w$ 表示特征的系数( $x$ 的参数)，可以看到正则化项是对系数做了限制。L1正则化和 L2正则化的说明如下：

L1正则化是指权值向量 $w$ 中各个元素的绝对值之和，通常表示为 $\left \| w \right \| _{1}= \sum \limits _{i}|w_i|$。
L2正则化是指权值向量 $w$ 中各个元素的平方和然后再求平方根，通常表示为 $\left \| w \right \| _{2}^{2}= \sqrt[2]{\sum \limits _{i}|w_{i}|^{2} }$ 。
一般都会在正则化项之前添加一个系数 $\lambda$ 。

　　由于增加正则化项，因此权重矩阵的值减小，因为它假定权重矩阵较小的神经网络会导致模型更简单。因此，它也将在一定程度上减少过度拟合。

3.1 L1 & L2 正则化的作用

　　L1正则化可以使得参数稀疏化，即得到的参数是一个稀疏矩阵，可用于特征选择。

稀疏性：模型很多参数是 $0$。通常机器学习中特征数量很多，如文本处理时，如果将一个词组作为一个特征，那么特征数量会达到上万个。在预测或分类时，那么多特征显然难以选择，但是如果代入这些特征得到的模型是一个稀疏模型，很多参数是 $0$ ，表示只有少数特征对这个模型有贡献，绝大部分特征是没有贡献的，即使去掉对模型也没什么影响，此时可以只关注系数是非零值的特征。相当于对模型进行一次特征选择，只留下一些比较重要的特征，提高模型的泛化能力，降低过拟合的可能。

　　L2正则化可以防止模型过拟合(overfitting)；一定程度上，L1也可以防止过拟合。

3.2 L1正则化与稀疏性

　　　　$Cost \ function =Loss+\lambda\ast \sum_ \limits{i=1} \|w_i \| $

事实上，”带正则项”和“带约束条件”是等价的。
为了约束 $w$ 的可能取值空间从而防止过拟合，我们为该最优化问题加上一个约束，就是 $w$ 的 L1范数不能大于 $m$ ：

　　　　$\begin{cases}\underset{w}{min} \ J(w;X,y)= \min \sum_ \limits{i=1}^{n}(w^Tx_i - y_i)^2 \\ s.t. \|w\|_1 \leqslant m.\end{cases}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (3)$

问题转化成带约束条件的凸优化问题，写出拉格朗日函数:

　　　　$\sum_ \limits{i=1}^{n}(w^Tx_i - y_i)^2 + \lambda (\|w\|_1-m)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (4)$

设 $W_*$ 和 $\lambda_*$ 是原问题的最优解，则根据 KKT 条件得：

　　　　$\begin{cases} 0 = \nabla_w[\sum_ \limits{i=1}^{n}(W_*^Tx_i - y_i)^2 + \lambda_* (\|w\|_1-m)] \\ 0 \leqslant \lambda_*.\end{cases}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (5)$

设L1正则化损失函数：$J = J_0 + \lambda \sum_ \limits {i} |w_i|$，其中$J_0 = \sum_ \limits {i=1}^{n}(w^Tx_i - y_i)^2$是原始损失函数，加号后面的一项是 L1正则化项，$\lambda$ 是正则化系数。
注意到L1正则化是权值的绝对值之和，$J$ 是带有绝对值符号的函数，因此 $J$ 是不完全可微的。任务是要通过一些方法(如梯度下降)求出损失函数的最小值。在原始损失函数$J_0$ 后添加 L1正则化项，相当于对 $J_0$ 做了一个约束。令 $L=\lambda \sum_ \limits i|w_i|$ ，则 $J=J_0+L$ ，此时任务变成在 $L$ 约束下求出 $J_0$ 取最小值的解。
假设在二维的情况，即只有两个权值 $w_1$ 和 $w_2$ ，求解 $J_0$ 的过程可以画出等值线，同时 L1正则化的函数 $ L=|w_1|+|w_2|<=m $ 可以在 $w_1$ 、$w_2$ 的二维平面上画出来。如下图：

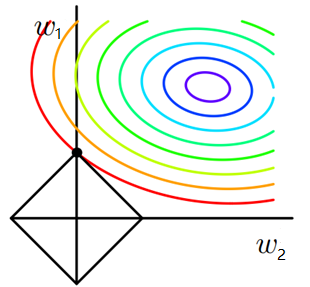
上图中等值线是 $J_0$ 的等值线，黑色方形是函数 $L$ 的图形。在图中，当 $J_0$ 等值线与图形 $L$ 首次相交的地方就是最优解。上图中 $J_0$ 与 $L$ 在 $L$ 的一个顶点处相交，这个顶点就是最优解。注意到这个顶点的值是 $(w1,w2)=(0,w2)$ 。可以直观想象，因为L函数有很多突出的角(二维情况下四个，多维情况下更多)，$J_0$ 与这些角接触的机率会远大于与L其它部位接触的机率，而在这些角上，会有很多权值等于 $0$，这就是为什么 $L1$ 正则化可以产生稀疏模型，进而可以用于特征选择。

Q:那么得到稀疏模型有什么好处呢？稀疏模型是指模型参数矩阵中有很多参数为0，只有少数参数是非零值的。机器学习中特征向量的维数一般很大，在预测或分类时，那么多特征显然难以选择，但是如果代入这些特征得到的模型是一个稀疏模型，表示只有少数特征对这个模型有贡献，绝大部分特征很大程度上是噪声特征，其没有贡献或贡献微小（因为它们前面的系数是0或者是很小的值，即使去掉对模型也没有什么影响），此时我们就可以只关注系数是非零值的特征。这就是稀疏模型与特征选择的关系。

3.3 L2正则化

　　　　$Cost \ function =Loss+\lambda\ast \sum_ \limits{i} ||w_i||_{2}^{2}$

　　同理，又L2正则化损失函数：$J = J_0 + \lambda \sum_ \limits{i} ||w_i||_{2}^{2}$，同样可画出其在二维平面的图像，如下：

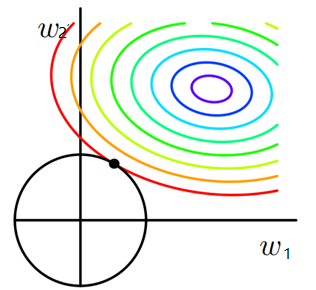
二维平面下 $L2$正则化的函数图形是个圆，与方形相比，被磨去了棱角。因此$J_0$与$L$相交时使得 $w_1$ 或 $w_2$ 等于零的机率小了许多，这就是为什么 $L2$正则化不具有稀疏性的原因。
L2正则化也称为权重衰减，因为它强制权重朝零衰减（但不完全为零）。

3.4 L1 & L2正则化总结

无论是L1 还是 L2正则化，正则化力度越大(正则化系数)，会放大惩罚项的值，使得曲线越平滑。
L1正则化：随着 $\lambda $ 值的增大，系数大部分为 $0$。
L2正则化：随着 $\lambda $ 值的增大，系数大部分减小，基本不为 $0$。
L1正则化用于特征之间有关联的情况，经过 L1正则化以后，系数更容易趋近于 $0$，这会导致部分特征值会被忽略掉，起到特征选择的作用。
L2正则化：适用于特征之间没有关联的情况。

4 其他相关正则化技术

4.1 Dropout

　　这是最有趣的正则化技术类型之一。它也产生非常好的结果，因此是深度学习领域中最常用的正则化技术。　

　　Dropout可以参考本博客《机器学习——正则化方法Dropout 》。

4.2 Data Augmentation

　　减少过度拟合的最简单方法是增加训练数据的大小。在机器学习中，我们无法增加训练数据的大小，因为标记的数据过于昂贵。

　　但是，现在让我们考虑一下我们正在处理图像。在这种情况下，有几种方法可以增加训练数据的大小-旋转图像，翻转，缩放，移动等。在下面的图像中，对手写数字数据集进行了一些转换。

　　这种技术称为数据增强。通常，这在提高模型的准确性方面提供了很大的飞跃。为了改善我们的预测，可以将其视为强制性的技巧。

为了防止过拟合现象，数据增强应运而生，接下来讨论下常见的数据增强方法。

常见方法

Color Jittering：对颜色的数据增强：图像亮度、饱和度、对比度变化（此处对色彩抖动的理解不知是否得当）；
PCA Jittering：首先按照RGB三个颜色通道计算均值和标准差，再在整个训练集上计算协方差矩阵，进行特征分解，得到特征向量和特征值，用来做PCA Jittering；
Random Scale：尺度变换；
Random Crop：采用随机图像差值方式，对图像进行裁剪、缩放；包括Scale Jittering方法（VGG及ResNet模型使用）或者尺度和长宽比增强变换；Horizontal/Vertical Flip：水平/垂直翻转；
Shift：平移变换；Rotation/Reflection：旋转/仿射变换；
Noise：高斯噪声、模糊处理；
Label shuffle：类别不平衡数据的增广，参见海康威视ILSVRC2016的report；另外，文中提出了一种Supervised Data Augmentation方法，有兴趣的朋友的可以动手实验下。

　　Data Augmentation可以参考本博客《机器学习——数据增强》。

Early stopping

　　Early stopping 是一种交叉验证策略，我们将训练集的一部分保留为验证集。当我们看到验证集的性能越来越差时，我们立即停止了对模型的训练。这称为提前停止。

　　早停法是一种被广泛使用的方法，在很多案例上都比正则化的方法要好。图1是我们经常看到论文中出现的图，也是使用早停法出现的一个结果。

　　其基本含义：在训练中计算模型在验证集上的表现，当模型在验证集上的表现开始下降的时候，停止训练，这样就能避免继续训练导致过拟合的问题。其主要步骤如下：

　　1. 将原始的训练数据集划分成训练集和验证集
　　2. 只在训练集上进行训练，并每个一个周期计算模型在验证集上的误差，例如，每15次epoch（mini batch训练中的一个周期）
　　3. 当模型在验证集上的误差比上一次训练结果差的时候停止训练
　　4. 使用上一次迭代结果中的参数作为模型的最终参数

然而，在现实中，模型在验证集上的误差不会像上图那样平滑，而是像下图一样：

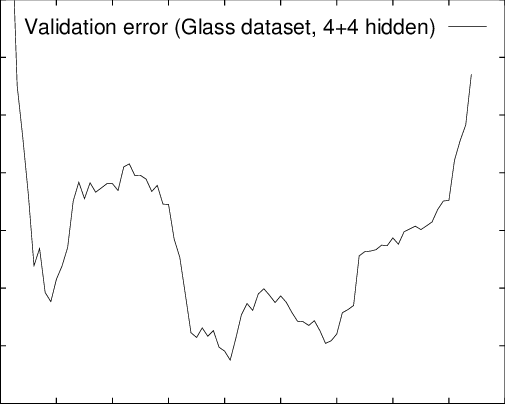
　　也就是说，模型在验证集上的表现可能咱短暂的变差之后有可能继续变好。上图在训练集迭代到400次的时候出现了16个局部最低。其中有4个最低值是它们所在位置出现的时候的最低点。其中全局最优大约出现在第205次迭代中。首次出现最低点是第45次迭代。相比较第45次迭代停止，到第400次迭代停止的时候找出的最低误差比第45次提高了1.1%，但是训练时间大约是前者的7倍。但是，并不是所有的误差曲线都像上图一样，有可能在出现第一次最低点之后，后面再也没有比当前最低点更低的情况了。所以我们看到，早停法主要是训练时间和泛化错误之间的权衡。尽管如此，也有某些停止标准也可以帮助我们寻找更好的权衡。

如何使用早停法

停止标准简介

停止标准有很多，也很灵活，大约有三种。在给出早停法的具体标准之前，我们先确定一下符号。假设我们使用

停止标准选择规则

一般情况下，“较慢”的标准会相对而言在平均水平上表现略好，可以提高泛化能力。然而，这些标准需要较长的训练时间。其实，总体而言，这些标准在系统性的区别很小。主要选择规则包括：

除非较小的提升也有很大价值，负责选择较快的停止标准
为了最大可能找到一个好的方案，使用GL标准
为了最大化平均解决方案的质量，如果网络只是过拟合了一点点，可以使用PQ标准，否则使用UP标准

参考文献

1 深入理解L1、L2正则化

2 深入理解L1、L2正则化

posted @ 2021-02-27 18:25 图神经网络阅读(756) 评论(0) 编辑收藏举报

刷新页面返回顶部

Blair