三角形外心的坐标公式

三角形外心的坐标公式

外心

三角形外接圆的圆心叫做三角形的外心。三角形外接圆的圆心也就是三角形三边垂直平分线的交点，三角形的三个顶点就在这个外接圆上。

 

 

 

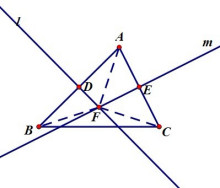
证明F在BC的中垂线上：

∵l、m分别为线段AB、AC的中垂线

∴AF=BF=CF

∴BC中垂线必过点F

给定三角形三个顶点的坐标，如何求三角形的外心的坐标呢？

例如 ：给定a（x1,y1） b（x2,y2） c（x3,y3）求外接圆心坐标O（x，y）
1. 首先，外接圆的圆心是三角形三条边的垂直平分线的交点，我们根据圆心到顶点的距离相等，可以列出以下方程：
       (x1-x)*(x1-x)-(y1-y)*(y1-y)=(x2-x)*(x2-x)+(y2-y)*(y2-y);
       (x2-x)*(x2-x)+(y2-y)*(y2-y)=(x3-x)*(x3-x)+(y3-y)*(y3-y);
2.化简得到：
        2*(x2-x1)*x+2*(y2-y1)y=x2^2+y2^2-x1^2-y1^2;
        2*(x3-x2)*x+2*(y3-y2)y=x3^2+y3^2-x2^2-y2^2;
        　 令　　　　　　　 A1=2*(x2-x1)；
            B1=2*(y2-y1)；
            C1=x2^2+y2^2-x1^2-y1^2;
            A2=2*(x3-x2)；
            B2=2*(y3-y2)；
            C2=x3^2+y3^2-x2^2-y2^2;
            即
                A1*x+B1y=C1;
                A2*x+B2y=C2;
3.最后根据克拉默法则：
          x=((C1*B2)-(C2*B1))/((A1*B2)-(A2*B1))；
          y=((A1*C2)-(A2*C1))/((A1*B2)-(A2*B1))；
因此，x，y为最终结果；
对于空间中的三角形，只不过最后解方程组的时候是三元方程组
Ps：克拉默法则可以用向量积和数量积的方法证明，也可以用高等代数的知识证明

 

 

 

 

代码：

#define double db
#define f(x,y) (x*x+y*y)
pair<db,db> fun(db x1,db y1,db x2,db y2,db x3,db y3){
    cin>>x1>>y1>>x2>>y2>>x3>>y3;
    db d1=f(x2,y2)-f(x1,y1),d2=f(x3,y3)-f(x2,y2);
    db fm=2*((y3-y2)*(x2-x1)-(y2-y1)*(x3-x2));
    db ans_x=((y3-y2)*d1-(y2-y1)*d2)/fm;
    db ans_y=((x2-x1)*d2-(x3-x2)*d1)/fm;
    return make_pair(ans_x,ans_y);
}