同余定理与逆元

同余定理：

数论中的重要概念。给定一个正整数m，如果两个整数a和b满足a-b能够被m整除，即(a-b)/m得到一个整数，

那么就称整数a与b对模m同余，记作a≡b(mod m)。对模m同余是整数的一个等价关系。

同余的主要性质：

 

逆元

利用费马小定理计算逆元

费马小定理：如果p是质数（素数），并且gcd(a,p) == 1, 那么就会满足下面的式子 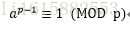，当然了，既然p已经是素数，

那么如果a < p那么就一定会满足这个式子，既然这样我们要得到 a^-1 我们就可以利用上面的式子来计算inv(a) : a^(p-2) = inv(a) (mod p)

这样我们就得到了我们需要的逆元：

long long q_pow(long long a,long long b,long long p)
{
    long long res = 1;
    while(b)
    {
        if(b&1)
        {
            res = (res*a)%p;
        }
        a = (a*a)%p;
        b>>=1;
    }
    return res;
}
long long inverse(long long a,long long p)
{
    return q_pow(a,p-2,p);
}