平衡二叉树详解

平衡二叉树详解

简介

平衡二叉树（Balanced Binary Tree）具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。平衡二叉树的常用实现方法有红黑树、AVL、替罪羊树、Treap、伸展树等。 其中最为经典当属AVL树，我们

总计而言就是：平衡二叉树是一种二叉排序树，其中每一个结点的左子树和右子树的高度差至多等于1。

性值

AVL树具有下列性质的二叉树（注意，空树也属于一种平衡二叉树）：

l  它必须是一颗二叉查找树

l  它的左子树和右子树都是平衡二叉树，且左子树和右子树的深度之差的绝对值不超过1。

l  若将二叉树节点的平衡因子BF定义为该节点的左子树的深度减去它的右子树的深度，则平衡二叉树上所有节点的平衡因子只可能为-1,0,1.

l  只要二叉树上有一个节点的平衡因子的绝对值大于1，那么这颗平衡二叉树就失去了平衡。

实现

平衡二叉树不平衡的情形：

把需要重新平衡的结点叫做α，由于任意两个结点最多只有两个儿子，因此高度不平衡时，α结点的两颗子树的高度相差2.容易看出，这种不平衡可能出现在下面4中情况中：

1.对α的左儿子的左子树进行一次插入

2.对α的左儿子的右子树进行一次插入

3.对α的右儿子的左子树进行一次插入

4.对α的右儿子的右子树进行一次插入

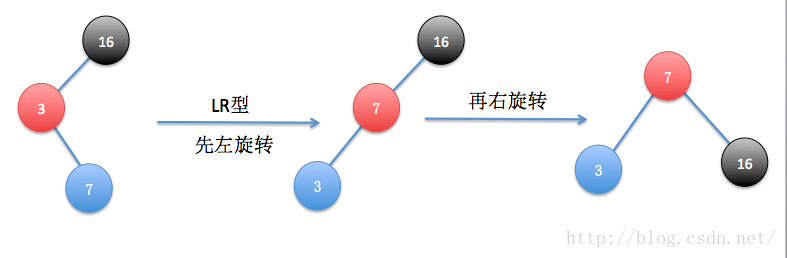
（1）LR型

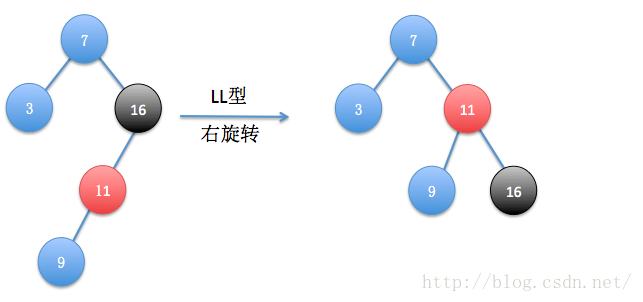
（2）LL型

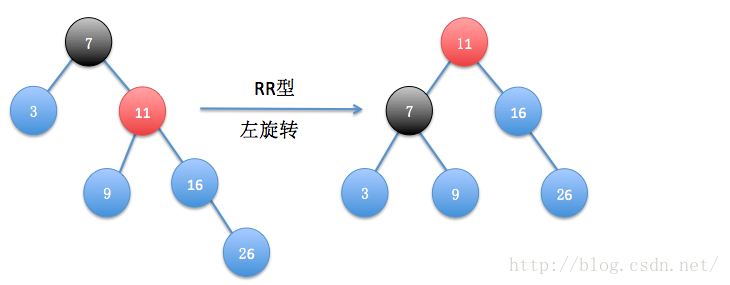
（3）RR型

 

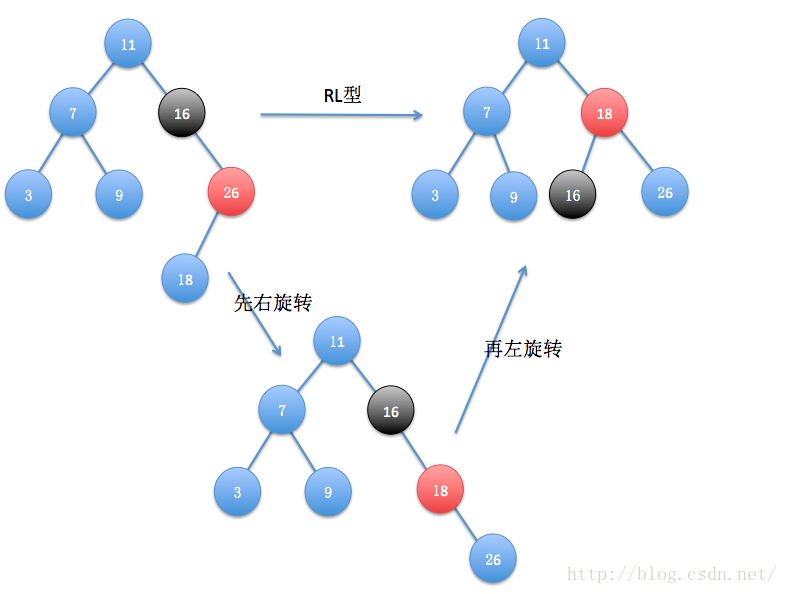
（4）RL型

完整代码

#include<stdio.h>
#include<stdlib.h>
  
//结点设计 
typedef struct Node {
    int key;
    struct Node *left;
    struct Node *right;
    int height;
} BTNode;
  
int height(struct Node *N) {
    if (N == NULL)
        return 0;
    return N->height;
}
  
int max(int a, int b) {
    return (a > b) ? a : b;
}
  
BTNode* newNode(int key) {
    struct Node* node = (BTNode*)malloc(sizeof(struct Node));
    node->key = key;
    node->left = NULL;
    node->right = NULL;
    node->height = 1;
    return(node);
}
  
//ll型调整 
BTNode* ll_rotate(BTNode* y) {
    BTNode *x = y->left;
    y->left = x->right;
    x->right = y;
  
    y->height = max(height(y->left), height(y->right)) + 1;
    x->height = max(height(x->left), height(x->right)) + 1;
  
    return x;
}
  
//rr型调整 
BTNode* rr_rotate(BTNode* y) {
    BTNode *x = y->right;
    y->right = x->left;
    x->left = y;
  
    y->height = max(height(y->left), height(y->right)) + 1;
    x->height = max(height(x->left), height(x->right)) + 1;
  
    return x;
}
  
//判断平衡
int getBalance(BTNode* N) {
    if (N == NULL)
        return 0;
    return height(N->left) - height(N->right);
}
  
//插入结点&数据
BTNode* insert(BTNode* node, int key) {
    if (node == NULL)
        return newNode(key);
  
    if (key < node->key)
        node->left = insert(node->left, key);
    else if (key > node->key)
        node->right = insert(node->right, key);
    else
        return node;
  
    node->height = 1 + max(height(node->left), height(node->right));
  
    int balance = getBalance(node);
  
    if (balance > 1 && key < node->left->key) //LL型
        return ll_rotate(node);
  
    if (balance < -1 && key > node->right->key)     //RR型
        return rr_rotate(node);
  
    if (balance > 1 && key > node->left->key) {   //LR型
        node->left = rr_rotate(node->left);
        return ll_rotate(node);
    }
  
    if (balance < -1 && key < node->right->key) {   //RL型
        node->right = ll_rotate(node->right);
        return rr_rotate(node);
    }
  
    return node;
}
  
//遍历
void preOrder(struct Node *root) {
    if (root != NULL) {
        printf("%d ", root->key);
        preOrder(root->left);
        preOrder(root->right);
    }
}
  
int main() {
    BTNode *root = NULL;
  
    root = insert(root, 2);
    root = insert(root, 1);
    root = insert(root, 0);
    root = insert(root, 3);
    root = insert(root, 4);
    root = insert(root, 4);
    root = insert(root, 5);
    root = insert(root, 6);
    root = insert(root, 9);
    root = insert(root, 8);
    root = insert(root, 7);
  
    printf("前序遍历：");
    preOrder(root);
    return 0;
}