并查集

并查集

一、关于并查集

1. 定义

并查集(Disjoint-Set)是一种可以动态维护若干个不重叠的集合，并支持合并与查询两种操作的一种数据结构。

2. 基本操作

1. 合并(Union/Merge)：合并两个集合。
2. 查询(Find/Get)：查询元素所属集合。
实际操作时，我们会使用一个点来代表整个集合，即一个元素的根结点(可以理解为父亲)。

3. 具体实现

我们建立一个数组fa[ ]或pre[ ]表示一个并查集，fa[i]表示i的父节点。
初始化：每一个点都是一个集合，因此自己的父节点就是自己fa[i]=i
查询：每一个节点不断寻找自己的父节点，若此时自己的父节点就是自己，那么该点为集合的根结点，返回该点。
修改：合并两个集合只需要合并两个集合的根结点，即fa[RootA]=RootB，其中RootA,RootB是两个元素的根结点。

路径压缩：
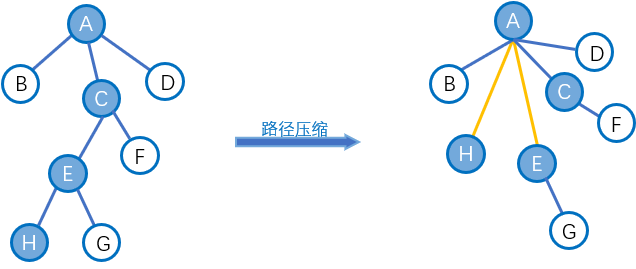
实际上，我们在查询过程中只关心根结点是什么，并不关心这棵树的形态(有一些题除外)。因此我们可以在查询操作的时候将访问过的每个点都指向树根，这样的方法叫做路径压缩，单次操作复杂度为O(logN)O(logN)。
结合下图食用更好(图为状态压缩的过程)：

二、代码实现

初始化的模板：

for(int i=1;i<=n;i++) pre[i]=i;

查询的模板(含路径压缩)：

int Find(int x){
    if(x==pre[x]) return x;
    return pre[x]=Find(pre[x]);
}

 

合并的模板：

void merge(int x,int y){
    int fx=Find(x),fy=Find(y);
    if(fx!=fy) pre[fx]=fy;
}
//主函数内
merge(a,b);