图论---DFS
1. 图的遍历
在理解DFS算法之前,我们首先需要对什么是遍历进行了解,遍历的概念就是:从某一个点出发(一般是首或尾),依次将数据结构中的每一个数据访问且只访问一遍。
2. DFS简介
DFS(Depth-First-Search,深度优先搜索)算法的具体做法是:从某个点一直往深处走,走到不能往下走之后,就回退到上一步,直到找到解或把所有点走完。
在实现这一个依次的访问顺序时,操作动作存储与数据结构(栈)的思想及其相似,同时也由于栈的性质,我们可以通过递归来简化栈的创建,因此DFS算法的两种做法分别时利用栈或者递归实现。
算法步骤(递归或栈实现)
a)访问指定起始地点。
b)若当前访问顶点的邻接顶点有未被访问的顶点,就任选一个访问。如果没有就回退到最近访问的顶点,直到与起始顶点相通的所有点被遍历完。
c)若途中还有顶点未被访问,则再选一个点作为起始顶点,并重复前面的步骤。
3. 图的DFS
我们直接以案例进行讲解,就本图而言,其访问顺序可以是(不唯一):1-2-4-5-3
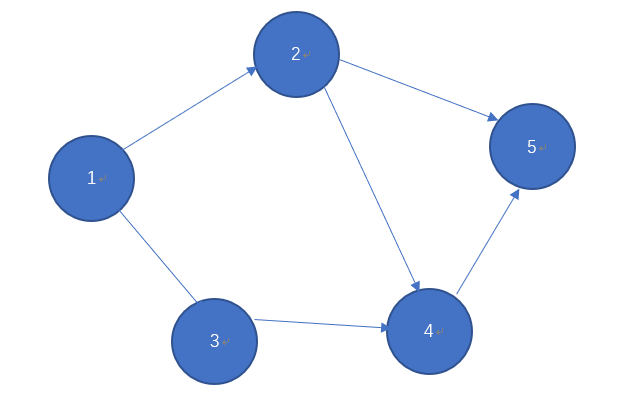
首先从1开始,1结点处可以访问2,3两个结点,那么按照我们自定义的优先顺序线访问2结点,此时,2结点有4,5两个结点访问,依旧按次序访问呢4结点,4结点可以访问5结点,5结点无法继续向下访问故结束访问,并回退4结点,4结点无法没有其他分支且自己已被访问故又退回2结点,2结点的两个分支4,5结点均已被访问,故再退回1结点,此时只有3结点未被访问,访问3结点,最终得到次序:1-2-4-5-3
4.相关代码
DFS算法的相关模板如下:
void dfs()//参数用来表示状态
{
if(到达终点状态)
{
...//根据需求添加
return;
}
if(越界或者是不合法状态)
return;
if(特殊状态)//剪枝,去除一些不需要访问的场景,不一定i俺家
return ;
for(扩展方式)
{
if(扩展方式所达到状态合法)
{
修改操作;//根据题意来添加
标记;
dfs();
(还原标记);
//是否还原标记根据题意
//如果加上(还原标记)就是 回溯法
}
}
}
5. 图的DFS代码:
#include<iostream>
using namespace std;
#define matrix_size 20
typedef struct {
int weight;
}AdjMatrix[matrix_size][matrix_size];
struct MGraph{
int vex[matrix_size];
AdjMatrix arcs;
int vexnum,arcnum;
};
bool visited[matrix_size];
int LocateVex(MGraph *G ,int v){
int i;
for ( i = 0; i < G->vexnum; i++)
{
if (G->vex[i]==v)
{
break;
}
}
if (i>G->vexnum)
{
cout<<"not such vertex"<<endl;
return -1;
}
return i;
}
//构造无向图
void CreateDN(MGraph *G){
cin>>G->vexnum>>G->arcnum;
for (int i = 0; i < G->vexnum; i++)
{
cin>>G->vex[i];
}
for (int i=0; i<G->vexnum; i++) {
for (int j=0; j<G->vexnum; j++) {
G->arcs[i][j].weight=0;
}
}
for (int i = 0; i < G->arcnum; i++)
{
int v1,v2;
cin>>v1>>v2;
int n=LocateVex(G,v1);
int m=LocateVex(G,v2);
if (m==-1||n==-1)
{
cout<<"not this vertex"<<endl;
return ;
}
G->arcs[n][m].weight=1;
G->arcs[m][n].weight=1;
}
return ;
}
//输出函数
void PrintGrapth(MGraph G)
{
for (int i = 0; i < G.vexnum; i++)
{
for (int j = 0; j < G.vexnum; j++)
{
cout<<G.arcs[i][j].weight<<" ";
}
cout<<endl;
}
}
void visitVex(MGraph G,int v){
cout<<G.vex[v];
}
int FirstAdjVex(MGraph G,int v){
for (int i = 0; i < G.vexnum; i++)
{
//查找与数组下标为v的顶点之间有边的顶点,返回它在数组中的下标
if (G.arcs[v][i].weight)
{
return i;
}
}
return -1;
}
int NextAdjVex(MGraph G,int v,int w)
{
//从前一个访问位置w的下一个位置开始,查找之间有边的顶点
for(int i = w+1; i<G.vexnum; i++){
if(G.arcs[v][i].weight){
return i;
}
}
return -1;
}
void DFS(MGraph G,int v){
visited[v]=true;
visitVex(G,v);
for (int w = FirstAdjVex(G,v); w >0; w= NextAdjVex(G,v,w))
{
if (!visited[w])
{
DFS(G,w);
}
}
}
//深度优先搜索
void DFSTraverse(MGraph G){//
int v;
//将用做标记的visit数组初始化为false
for( v = 0; v < G.vexnum; ++v){
visited[v] = false;
}
//对于每个标记为false的顶点调用深度优先搜索函数
for( v = 0; v < G.vexnum; v++){
//如果该顶点的标记位为false,则调用深度优先搜索函数
if(!visited[v]){
DFS( G, v);
}
}
}
int main() {
MGraph G;//建立一个图的变量
CreateDN(&G);//初始化图
DFSTraverse(G);//深度优先搜索图
return 0;
}
因上求缘,果上努力~~~~ 作者:别关注我了,私信我吧,转载请注明原文链接:https://www.cnblogs.com/BlairGrowing/p/13639962.html




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· winform 绘制太阳,地球,月球 运作规律
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 上周热点回顾(3.3-3.9)
· 超详细:普通电脑也行Windows部署deepseek R1训练数据并当服务器共享给他人