排序算法
排序算法
| 冒泡排序 | O(n2) |
| 选择排序 | O(n2) |
| 插入排序 | O(n2) |
| 希尔排序 | O(n1.5) |
| 快速排序 | O(N*logN) |
| 归并排序 | O(N*logN) |
| 堆排序 | O(N*logN) |
| 基数排序 | O(d(n+r)) |
一. 冒泡排序(BubbleSort)
基本思想:两个数比较大小,较大的数下沉,较小的数冒起来。
过程:
- 比较相邻的两个数据,如果第二个数小,就交换位置。
- 从后向前两两比较,一直到比较最前两个数据。最终最小数被交换到起始的位置,这样第一个最小数的位置就排好了。
- 继续重复上述过程,依次将第2.3...n-1个最小数排好位置。

//冒泡排序
void BubbleSort(int [] arr,int len){
for (int i = 0; i < len; i++)
{
for (int j = len-1; j> i; j--)
{
if (arr[j]<arr[j-1]) swap(arr[j],arr[j-1]);
}
}
}
优化:
针对问题:
数据的顺序排好之后,冒泡算法仍然会继续进行下一轮的比较,直到arr.length-1次,后面的比较没有意义的。
方案:
设置标志位flag,如果发生了交换flag设置为true;如果没有交换就设置为false。
这样当一轮比较结束后如果flag仍为false,即:这一轮没有发生交换,说明数据的顺序已经排好,没有必要继续进行下去。
public static void BubbleSort1(int [] arr){
int temp;//临时变量
boolean flag;//是否交换的标志
for(int i=0; i<arr.length-1; i++){ //表示趟数,一共 arr.length-1 次
// 每次遍历标志位都要先置为false,才能判断后面的元素是否发生了交换
flag = false;
for(int j=arr.length-1; j>i; j--){ //选出该趟排序的最大值往后移动
if(arr[j] < arr[j-1]){
temp = arr[j];
arr[j] = arr[j-1];
arr[j-1] = temp;
flag = true; //只要有发生了交换,flag就置为true
}
}
// 判断标志位是否为false,如果为false,说明后面的元素已经有序,就直接return
if(!flag) break;
}
}
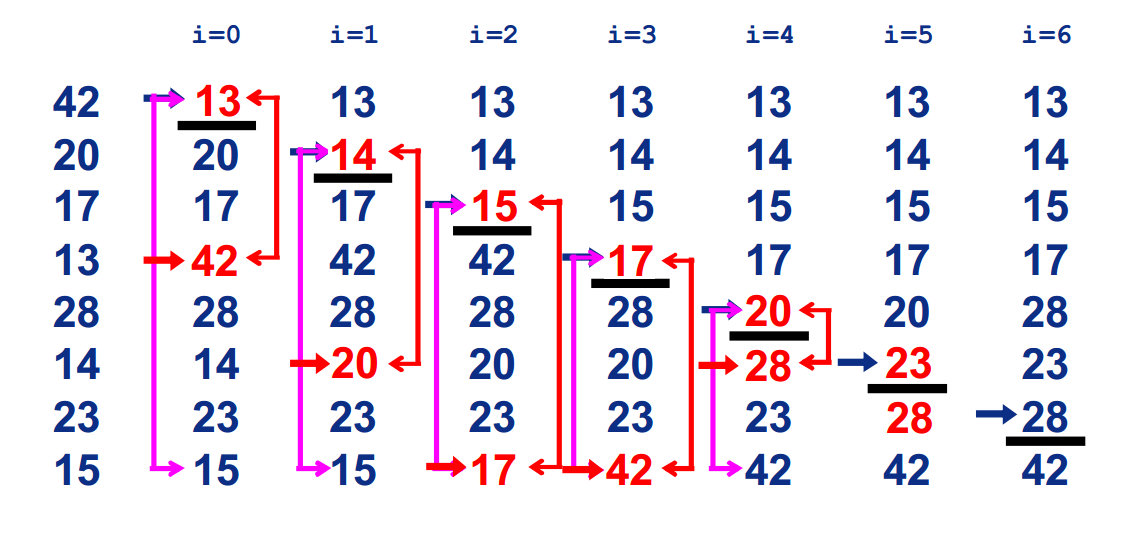
二. 选择排序(SelctionSort)
基本思想:
在长度为N的无序数组中,第一次遍历n-1个数,找到最小的数值与第一个元素交换;
第二次遍历n-2个数,找到最小的数值与第二个元素交换;
第n-1次遍历,找到最小的数值与第n-1个元素交换,排序完成。
//选择排序
void select_sort(int arr[],int len){
for (int i = 0; i < len; i++)
{
int minIndex =i;
for (int j = i+1; j < len; j++)
{
if (arr[j]<arr[minIndex])
{
minIndex=j;
}
}
if (minIndex!=i)
{
swap(arr[minIndex],arr[i]);
}
}
}
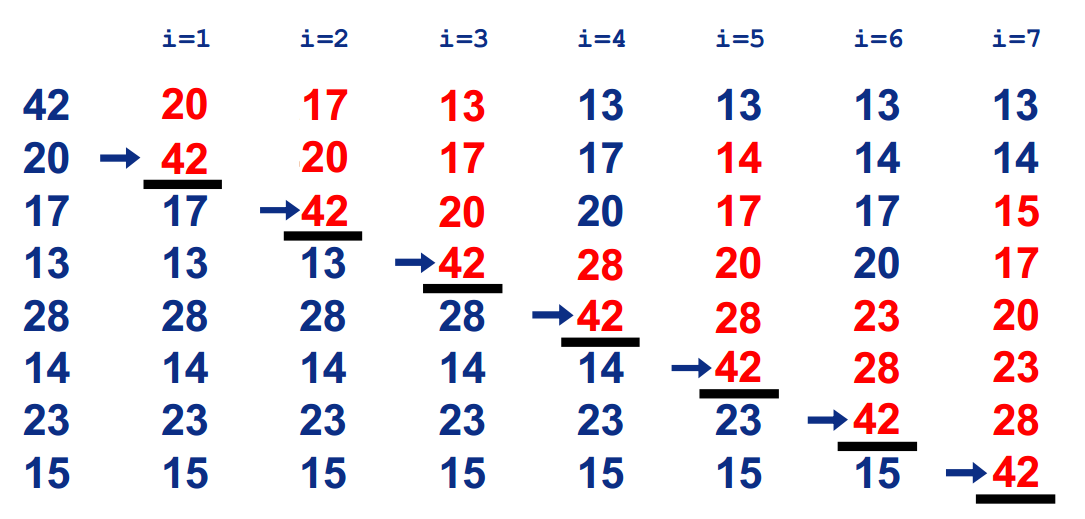
三. 插入排序(Insertion Sort)
基本思想:
在要排序的一组数中,假定前n-1个数已经排好序,现在将第n个数插到前面的有序数列中,使得这n个数也是排好顺序的。如此反复循环,直到全部排好顺序。
过程:
//插入排序
void insert_sort(int arr[],int lenth){
for(int i=0;i<len;i++){
//j=i+1是取拍好序后的第一个未排好序的元素
for (int j = i+1; j > 0; j--)
{
if (arr[j]<arr[j-1])
{
swap(arr[j],arr[j-1]);
}else
{
break;
}
}
}
}
四. 希尔排序(Shell Sort)
前言:
数据序列1: 13-17-20-42-28 利用插入排序,13-17-20-28-42. Number of swap:1;
数据序列2: 13-17-20-42-14 利用插入排序,13-14-17-20-42. Number of swap:3;
如果数据序列基本有序,使用插入排序会更加高效。
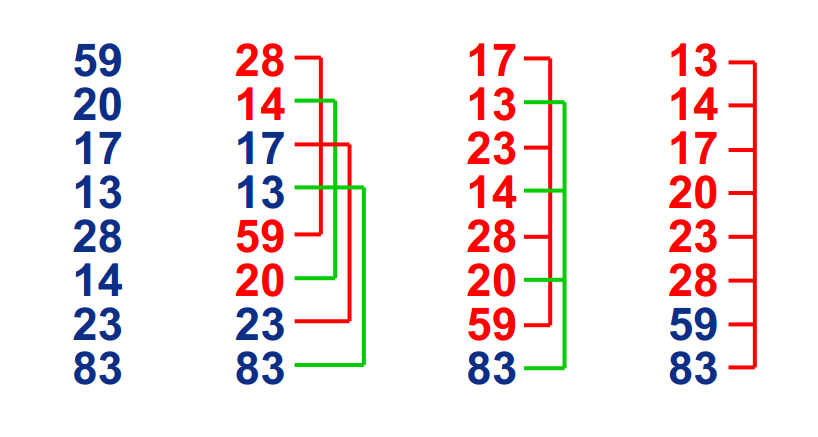
基本思想:
在要排序的一组数中,根据某一增量分为若干子序列,并对子序列分别进行插入排序。
然后逐渐将增量减小,并重复上述过程。直至增量为1,此时数据序列基本有序,最后进行插入排序。
过程:
//希尔排序
void shell_sort(int arr[],int len){
int incre = len;
while (true){
incre = incre/2;
for (int k = 0; k < incre; k++)
{
for (int i = k+incre; i < len; i+=incre)
{
for (int j = i; j > k; j-=incre)
{
if (arr[j]<arr[j-incre])
{
swap(arr[j],arr[j-incre]);
}else
{
break;
}
}
}
}
}
}
五. 快速排序(Quicksort)
基本思想:(分治)
- 先从数列中取出一个数作为key值;
- 将比这个数小的数全部放在它的左边,大于或等于它的数全部放在它的右边;
- 对左右两个小数列重复第二步,直至各区间只有1个数。
void quickSort(int a[],int l,int r){
if(l>r)return;
int i=1,j=r,key=a[l];
while(i<j){
while(i<j&&a[j]>=key){//从右向左找第一个小于key的值
j--;
}
if(i<j){
a[i]=a[j];
i++;
}
while (i<j&&a[i]<key)//从左向右找第一个大于key的值
{
i++;
}
if (i<j)
{
a[j]=a[i];
j--;
}
//i==j
a[i]=key;
quickSort(a,l,i-1);
quickSort(a,i+1,r);
}
}
六. 归并排序(Merge Sort)
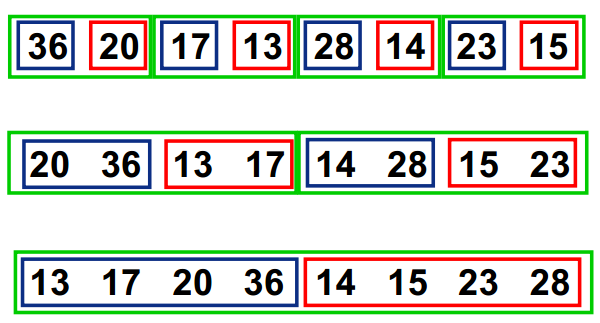
基本思想:
归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法的一个非常典型的应用。
首先考虑下如何将2个有序数列合并。这个非常简单,只要从比较2个数列的第一个数,谁小就先取谁,取了后就在对应数列中删除这个数。然后再进行比较,如果有数列为空,那直接将另一个数列的数据依次取出即可。
解决了上面的合并有序数列问题,再来看归并排序,其的基本思路就是将数组分成2组A,B,如果这2组组内的数据都是有序的,那么就可以很方便的将这2组数据进行排序。如何让这2组组内数据有序了?
可以将A,B组各自再分成2组。依次类推,当分出来的小组只有1个数据时,可以认为这个小组组内已经达到了有序,然后再合并相邻的2个小组就可以了。这样通过先递归的分解数列,再合并数列就完成了归并排序。
public static void merge_sort(int a[],int first,int last,int temp[]){
if(first < last){
int middle = (first + last)/2;
merge_sort(a,first,middle,temp);//左半部分排好序
merge_sort(a,middle+1,last,temp);//右半部分排好序
mergeArray(a,first,middle,last,temp); //合并左右部分
}
}
//合并 :将两个序列a[first-middle],a[middle+1-end]合并
public static void mergeArray(int a[],int first,int middle,int end,int temp[]){
int i = first;
int m = middle;
int j = middle+1;
int n = end;
int k = 0;
while(i<=m && j<=n){
if(a[i] <= a[j]){
temp[k] = a[i];
k++;
i++;
}else{
temp[k] = a[j];
k++;
j++;
}
}
while(i<=m){
temp[k] = a[i];
k++;
i++;
}
while(j<=n){
temp[k] = a[j];
k++;
j++;
}
for(int ii=0;ii<k;ii++){
a[first + ii] = temp[ii];
}
}
七. 堆排序(HeapSort)
堆排序
堆排序是利用堆这种数据结构而设计的一种排序算法,堆排序是一种选择排序,它的最坏,最好,平均时间复杂度均为O(nlogn),它也是不稳定排序。首先简单了解下堆结构。
堆
堆是具有以下性质的完全二叉树:每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆。如下图:
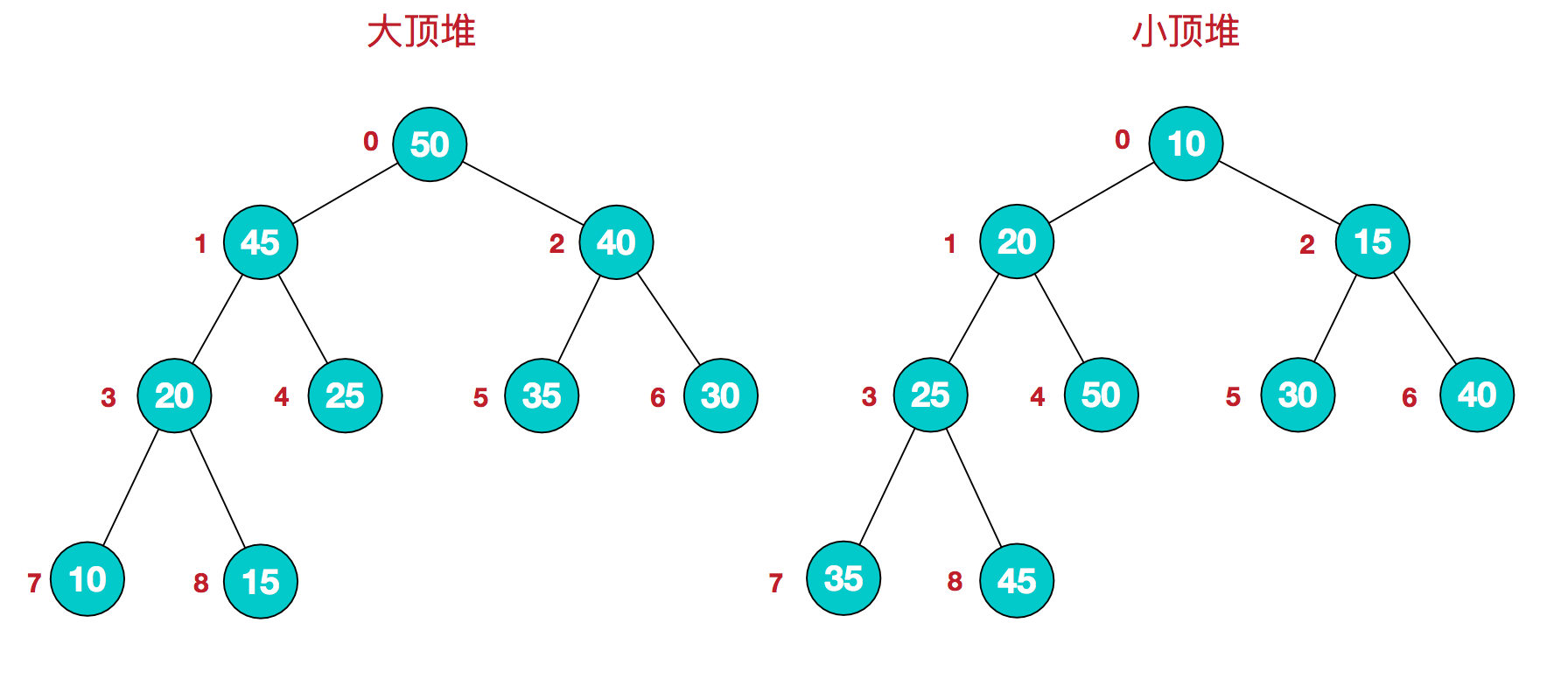
基本思想:
a.将无需序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆;
b.将堆顶元素与末尾元素交换,将最大元素"沉"到数组末端;
c.重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序。
package sortdemo;
import java.util.Arrays;
/**
* Created by chengxiao on 2016/12/17.
* 堆排序demo
*/
public class HeapSort {
public static void main(String []args){
int []arr = {9,8,7,6,5,4,3,2,1};
sort(arr);
System.out.println(Arrays.toString(arr));
}
public static void sort(int []arr){
//1.构建大顶堆
for(int i=arr.length/2-1;i>=0;i--){
//从第一个非叶子结点从下至上,从右至左调整结构
adjustHeap(arr,i,arr.length);
}
//2.调整堆结构+交换堆顶元素与末尾元素
for(int j=arr.length-1;j>0;j--){
swap(arr,0,j);//将堆顶元素与末尾元素进行交换
adjustHeap(arr,0,j);//重新对堆进行调整
}
}
/**
* 调整大顶堆(仅是调整过程,建立在大顶堆已构建的基础上)
* @param arr
* @param i
* @param length
*/
public static void adjustHeap(int []arr,int i,int length){
int temp = arr[i];//先取出当前元素i
for(int k=i*2+1;k<length;k=k*2+1){//从i结点的左子结点开始,也就是2i+1处开始
if(k+1<length && arr[k]<arr[k+1]){//如果左子结点小于右子结点,k指向右子结点
k++;
}
if(arr[k] >temp){//如果子节点大于父节点,将子节点值赋给父节点(不用进行交换)
arr[i] = arr[k];
i = k;
}else{
break;
}
}
arr[i] = temp;//将temp值放到最终的位置
}
public static void swap(int []arr,int a ,int b){
int temp=arr[a];
arr[a] = arr[b];
arr[b] = temp;
}
}
八.计数排序
算法的步骤如下:
第一步:找出原数组中元素值最大的,记为max。
第二步:创建一个新数组count,其长度是max加1,其元素默认值都为0。
第三步:遍历原数组中的元素,以原数组中的元素作为count数组的索引,以原数组中的元素出现次数作为count数组的元素值。
第四步:创建结果数组result,起始索引index。
第五步:遍历count数组,找出其中元素值大于0的元素,将其对应的索引作为元素值填充到result数组中去,每处理一次,count中的该元素值减1,直到该元素值不大于0,依次处理count中剩下的元素。
第六步:返回结果数组result。
public int[] countSort(int[] A) {
// 找出数组A中的最大值
int max = Integer.MIN_VALUE;
for (int num : A) {
max = Math.max(max, num);
}
// 初始化计数数组count
int[] count = new int[max+1];
// 对计数数组各元素赋值
for (int num : A) {
count[num]++;
}
// 创建结果数组
int[] result = new int[A.length];
// 创建结果数组的起始索引
int index = 0;
// 遍历计数数组,将计数数组的索引填充到结果数组中
for (int i=0; i<count.length; i++) {
while (count[i]>0) {
result[index++] = i;
count[i]--;
}
}
// 返回结果数组
return result;
}
优化版
基础版能够解决一般的情况,但是它有一个缺陷,那就是存在空间浪费的问题。
比如一组数据{101,109,108,102,110,107,103},其中最大值为110,按照基础版的思路,我们需要创建一个长度为111的计数数组,但是我们可以发现,它前面的[0,100]的空间完全浪费了,那怎样优化呢?
将数组长度定为max-min+1,即不仅要找出最大值,还要找出最小值,根据两者的差来确定计数数组的长度。
public int[] countSort2(int[] A) {
// 找出数组A中的最大值、最小值
int max = Integer.MIN_VALUE;
int min = Integer.MAX_VALUE;
for (int num : A) {
max = Math.max(max, num);
min = Math.min(min, num);
}
// 初始化计数数组count
// 长度为最大值减最小值加1
int[] count = new int[max-min+1];
// 对计数数组各元素赋值
for (int num : A) {
// A中的元素要减去最小值,再作为新索引
count[num-min]++;
}
// 创建结果数组
int[] result = new int[A.length];
// 创建结果数组的起始索引
int index = 0;
// 遍历计数数组,将计数数组的索引填充到结果数组中
for (int i=0; i<count.length; i++) {
while (count[i]>0) {
// 再将减去的最小值补上
result[index++] = i+min;
count[i]--;
}
}
// 返回结果数组
return result;
}
进阶版步骤
以数组A = {101,109,107,103,108,102,103,110,107,103}为例。
第一步:找出数组中的最大值max、最小值min。
第二步:创建一个新数组count,其长度是max-min加1,其元素默认值都为0。
第三步:遍历原数组中的元素,以原数组中的元素作为count数组的索引,以原数组中的元素出现次数作为count数组的元素值。
第四步:对count数组变形,新元素的值是前面元素累加之和的值,即count[i+1] = count[i+1] + count[i];。
第五步:创建结果数组result,长度和原始数组一样。
public int[] countSort3(int[] A) {
// 找出数组A中的最大值、最小值
int max = Integer.MIN_VALUE;
int min = Integer.MAX_VALUE;
for (int num : A) {
max = Math.max(max, num);
min = Math.min(min, num);
}
// 初始化计数数组count
// 长度为最大值减最小值加1
int[] count = new int[max-min+1];
// 对计数数组各元素赋值
for (int num : A) {
// A中的元素要减去最小值,再作为新索引
count[num-min]++;
}
// 计数数组变形,新元素的值是前面元素累加之和的值
for (int i=1; i<count.length; i++) {
count[i] += count[i-1];
}
// 创建结果数组
int[] result = new int[A.length];
// 遍历A中的元素,填充到结果数组中去
for (int j=0; j<A.length; j++) {
result[count[A[j]-min]-1] = A[j];
count[A[j]-min]--;
}
return result;
}
九.桶排序

templatevoid BucketSort(vector&A, int n)
{
int i ,j;
vector B[7]; //桶容器
for (i = 0; i < n; i++)
{
int temp = n*A[i];
B[temp].push_back(A[i]);
}
for (i = 0; i < n; i++)
sort(B[i].begin(), B[i].end()); //对每个桶排序
int index = 0;
for (i = 0; i < n; i++)
{
for (j = 0; j < B[i].size(); j++)
A[index++] = B[i][j];
}
}
int main(void)
{
vectorarr = { 0.897, 0.565, 0.656, 0.1234, 0.665, 0.3434 };
int n = arr.size();
BucketSort(arr, n);
for (auto i = 0; i < n; i++)
cout << arr[i] << " ";
cout << endl;
}
十.桶排序
基数排序图文说明
通过基数排序对数组{53, 3, 542, 748, 14, 214, 154, 63, 616},它的示意图如下:

在上图中,首先将所有待比较树脂统一为统一位数长度,接着从最低位开始,依次进行排序。
1. 按照个位数进行排序。
2. 按照十位数进行排序。
3. 按照百位数进行排序。
排序后,数列就变成了一个有序序列。
int maxbit(int data[], int n) //辅助函数,求数据的最大位数
{
int d = 1; //保存最大的位数
int p = 10;
for(int i = 0; i < n; ++i)
{
while(data[i] >= p)
{
p *= 10;
++d;
}
}
return d;
}
void radixsort(int data[], int n) //基数排序
{
int d = maxbit(data, n);
int *tmp = newint[n];
int *count = newint[10]; //计数器
int i, j, k;
int radix = 1;
for(i = 1; i <= d; i++) //进行d次排序
{
for(j = 0; j < 10; j++)
count[j] = 0; //每次分配前清空计数器
for(j = 0; j < n; j++)
{
k = (data[j] / radix) % 10; //统计每个桶中的记录数
count[k]++;
}
for(j = 1; j < 10; j++)
count[j] = count[j - 1] + count[j]; //将tmp中的位置依次分配给每个桶
for(j = n - 1; j >= 0; j--) //将所有桶中记录依次收集到tmp中
{
k = (data[j] / radix) % 10;
tmp[count[k] - 1] = data[j];
count[k]--;
}
for(j = 0; j < n; j++) //将临时数组的内容复制到data中
data[j] = tmp[j];
radix = radix * 10;
}
delete[]tmp;
delete[]count;
}
因上求缘,果上努力~~~~ 作者:图神经网络,转载请注明原文链接:https://www.cnblogs.com/BlairGrowing/p/13540147.html


