树的概念

树的概念

之前介绍的所有的数据结构都是线性存储结构。本章所介绍的树结构是一种非线性存储结构，存储的是具有“一对多”关系的数据元素的集合。

 

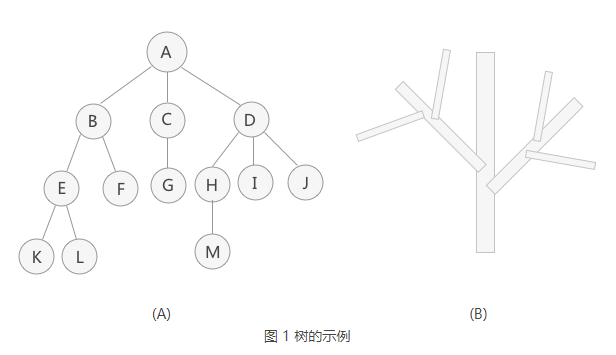
图 1(A) 是使用树结构存储的集合 {A,B,C,D,E,F,G,H,I,J,K,L,M} 的示意图。对于数据 A 来说，和数据 B、C、D 有关系；对于数据 B 来说，和 E、F 有关系。这就是“一对多”的关系。

基本术语

①结点： 数据元素 + 若干指向子树的分支

②结点的度: 分支的个数

③树的度: 树中所有结点的度的最大值

④叶子结点: 度为零的结点

⑤分支结点: 度大于零的结点

⑥(从根到结点的)路径：  由从根到该结点所经分支和结点构成。

⑦孩子结点： 一个结点的直接后继

⑧双亲结点: 一个结点的直接前驱

⑨兄弟结点: 同一双亲结点的孩子结点之间互称~ ~。

⑩ 堂兄弟、祖先结点、子孙结点

结点的层次: 假设根结点的层次为0 ，依次累加 。

树的深度： 树中 叶子 结点所在 的

有向树： 有确定的根；树根和子树根之间为有向关系。

有序树： 子树之间存在确定的次序关系。

无序树：子树之间不存在确定的次序关系。

森林： 是m m （ m≥0 ）棵互不相交的树的集合

 

二叉树定义：

满足以上两个条件的树型结构为 二叉树 。

①每个结点的度都不大于2；

②每个结点的孩子结点次序不能任意颠倒。

二叉树或为 空树 ， 或是由一个 根结点 加上两棵分别称为 左子树 和 右子树 的 、 互不相交的二叉树组成 。

                                       

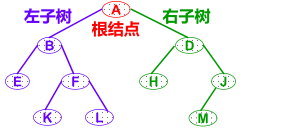
表示方法

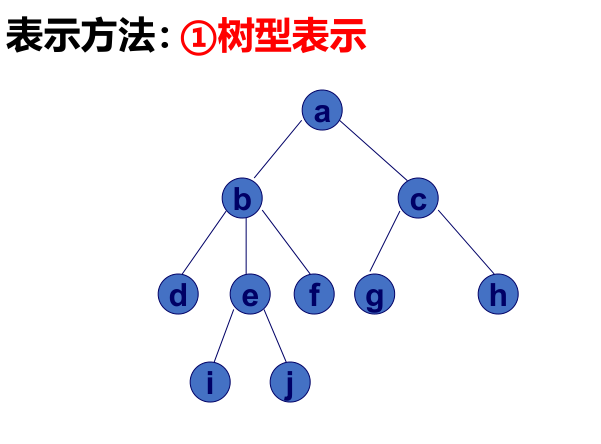
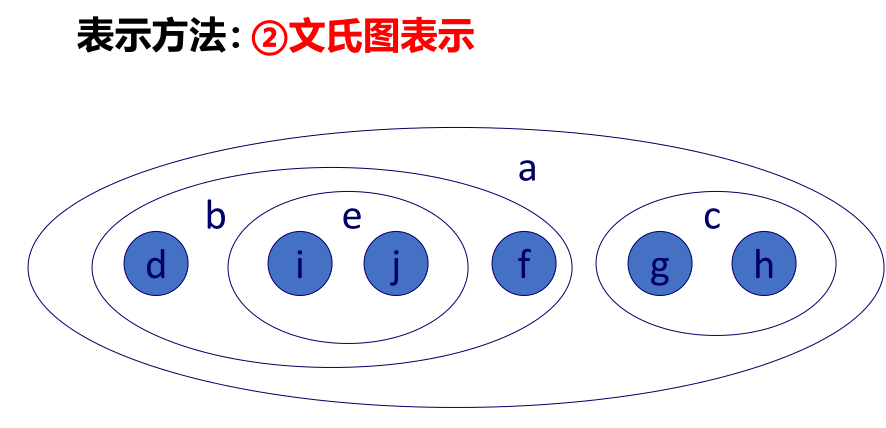
二叉树形态：

 

                   

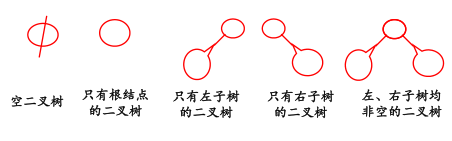
性质：

1 在二叉树的第 i 层上至多有2 ⁱ 个结点

用归纳法证明：

（1 ） 当 i = 0  层时，只有一个根结点： 2  ⁱ = 2 ⁰ = 1  ；

（2  ） 假设 i=k 时成立，即第k 层上至多有2  ^k 个结点；

（3 ） 那么第 k+1 层上最多有2 ^k × 2  个，即2 ^k+1 个 。

结论成立，证毕。

2 深度为 k 的二叉树上至多含 2 ^k+1 -1 个结点(k≥0)。

证明：

基于上一条性质，深度为 k 的二叉树上的结点数至多为

   

3 对任何一棵二叉树，若它含有n₀ 个叶子结点、n₂ 个度为 2 的结点，则必存在关系式：

 

           

   

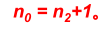
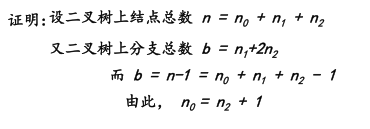
对于一个二叉树来说，除了度为 0 的叶子结点和度为 2 的结点，剩下的就是度为 1 的结点（设为 n₁），那么总结点 n=n₀+n₁+n₂。同时，对于每一个结点来说都是由其父结点分支表示的，假设树中分枝数为 B，那么总结点数 n=B+1。而分枝数是可以通过 n₁ 和 n₂ 表示的，即 B=n₁+2*n₂。所以，n 用另外一种方式表示为 n=n₁+2*n₂+1。

两种方式得到的 n 值组成一个方程组，就可以得出 n₀=n₂+1。

 

满二叉树

如果二叉树中除了叶子结点，每个结点的度都为 2，则此二叉树称为满二叉树。

                       

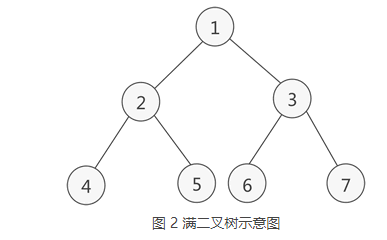
满二叉树除了满足普通二叉树的性质，还具有以下性质：

1. 满二叉树中第 i 层的节点数为 2^i-1 个。
2. 深度为 k 的满二叉树必有 2^k-1 个节点 ，叶子数为 2^k-1。
3. 满二叉树中不存在度为 1 的节点，每一个分支点中都两棵深度相同的子树，且叶子节点都在最底层。
4. 具有 n 个节点的满二叉树的深度为 log₂(n+1)。

完全二叉树

如果二叉树中除去最后一层节点为满二叉树，且最后一层的结点依次从左到右分布，则此二叉树被称为完全二叉树。

 

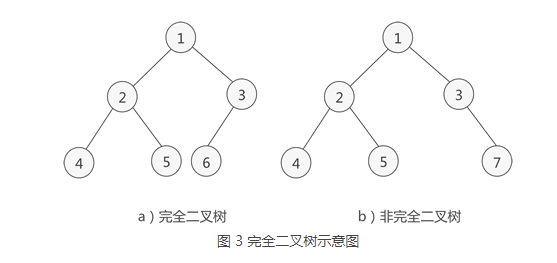
完全二叉树的性质

1) n 个结点的完全二叉树的深度为 ⌊log₂n⌋+1。

2)对于具有n个结点的完全二叉树，如果按照从上到 下和从左到右的顺序对树中的所有结点从1开始

进行编 号，则对于任意的序号为i的结点，有：

(1) 如果i=0，则它是根结点，它没有父结 ,如果i>0， 则它的父结点的下标为 [(i-1)/2];

(2) 如果2i+1≤n-1， 则下标为 则下标为i的结点的左子结点的下标为 2i+1; 否则，下标为i的结 点没有左子结点;

(3) 如果2i+2≤n-1，则下标为 则下标为i的结点的右 子结点的下标为 2i+2; 否则，下标为i的结 点没有右子结点。

 

关系：满二叉树必为完全二叉树，而完全二叉树不一定是满二叉树。

扩充的二叉树

 

                                   

 

 

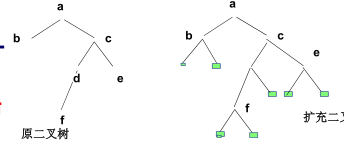
• 加 在扩充的二叉树里外部结点（叶结点）都是新增加 的结点

• 如果原二叉树有ｎ个结点，在扩充的二叉树里这n个结点的度数都是2。因此扩充的二叉树有 2n 条边，2n+1 个结点，除n 个原来二叉树结点，还有 n+1是新增加的外部结点

 

性质：

6 在扩充的二叉树里，新增加的外部结点的个数比原来的内部结点个数多1

                   

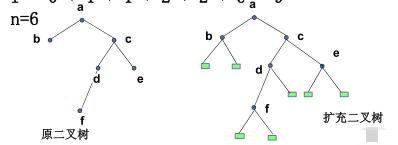
定义：外部路径长度E和I内部路径长度E = I + 2n

如下图的扩充二叉树中: :

E = 2 + 2 + 4 + 4 + 3 + 3 + 3 = 21

I =  0 + 1 +  1 +  2 + 2 + 3 = 9