BF算法(串模式匹配算法)
主串和子串
主串与子串:如果串 A(如 "shujujiegou")中包含有串 B(如 "ju"),则称串 A 为主串,串 B 为子串。主串与子串之间的关系可简单理解为一个串 "包含" 另一个串的关系。
实现串的模式匹配的算法主要有以下两种:
- 普通的模式匹配算法;
- 快速模式匹配算法;
BF算法原理
普通模式匹配算法,其实现过程没有任何技巧,就是简单粗暴地拿一个串同另一个串中的字符一一比对,得到最终结果。
例如,使用普通模式匹配算法判断串 A("abcac")是否为串 B("ababcabacabab")子串的判断过程如下:
首先,将串 A 与串 B 的首字符对齐,然后逐个判断相对的字符是否相等,如图 1 所示:
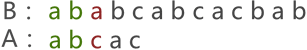
图 1 串的第一次模式匹配示意图
图 1 中,由于串 A 与串 B 的第 3 个字符匹配失败,因此需要将串 A 后移一个字符的位置,继续同串 B 匹配,如图 2 所示:
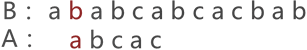
图 2 串的第二次模式匹配示意图
图 2 中可以看到,两串匹配失败,串 A 继续向后移动一个字符的位置,如图 3 所示:
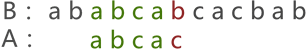
图 3 串的第三次模式匹配示意图
图 3 中,两串的模式匹配失败,串 A 继续移动,一直移动至图 4 的位置才匹配成功:

图 4 串模式匹配成功示意图
由此,串 A 与串 B 以供经历了 6 次匹配的过程才成功,通过整个模式匹配的过程,证明了串 A 是串 B 的子串(串 B 是串 A 的主串)。
接下来,我们要编写代码实现两个串的模式匹配(图 1 ~图 4)。
BF算法实现

链表形式:
//求串p 在串t 中第一次出现的位置,即p 的第一个元素在串t 中的序号(下标+1)
int index(LinkString t,LinkString p){
int i=0,j=0; //初始化
while (i<p->n&&j<t->n)
{
if(p->c[i]==t->c[j]){
++i,++j;
}else
{
j=j-i+1;
i=0;
}
}
if (i>=p->n)
{
return j-p->n+1;
}else
{
return 0;
}
}
顺序表形式
int index(LinkString t,LinkString p){
int i=0,j=0; //初始化
while (i<p->n&&j<t->n)
{
if(p->c[i]==t->c[j]){
++i,++j;
}else
{
j=j-i+1;
i=0;
}
}
if (i>=p->n)
{
return j-p->n+1;
}else
{
return 0;
}
}
BF算法时间复杂度
该算法最理想的时间复杂度 O(n),n 表示串 A 的长度,即第一次匹配就成功。
BF 算法最坏情况的时间复杂度为 O(n*m),n 为串 A 的长度,m 为串 B 的长度。例如,串 B 为 "0000000001",而串 A 为 "01",这种情况下,两个串每次匹配,都必须匹配至串 A 的最末尾才能判断匹配失败,因此运行了 n*m 次。
总结
BF 算法的实现过程很 "无脑",不包含任何技巧,在对数据量大的串进行模式匹配时,算法的效率很低。
因上求缘,果上努力~~~~ 作者:图神经网络,转载请注明原文链接:https://www.cnblogs.com/BlairGrowing/p/13034497.html


