访问所有点的最小时间

　　平面上有 n 个点，点的位置用整数坐标表示 points[i] = [xi, yi]。请你计算访问所有这些点需要的最小时间（以秒为单位）。

你可以按照下面的规则在平面上移动：

　　每一秒沿水平或者竖直方向移动一个单位长度，或者跨过对角线（可以看作在一秒内向水平和竖直方向各移动一个单位长度）。

必须按照数组中出现的顺序来访问这些点。

 

 

 

示例 1：

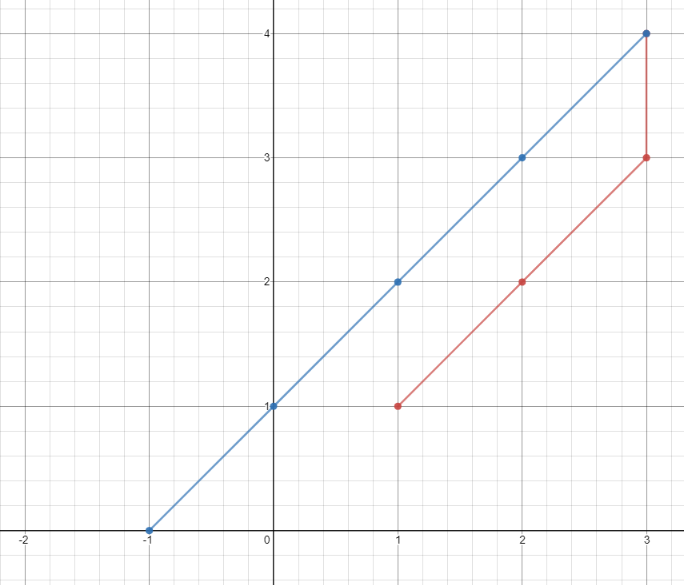
　　输入：points = [[1,1],[3,4],[-1,0]]
　　输出：7
　　解释：一条最佳的访问路径是： [1,1] -> [2,2] -> [3,3] -> [3,4] -> [2,3] -> [1,2] -> [0,1] -> [-1,0]
　　从 [1,1] 到 [3,4] 需要 3 秒
　　从 [3,4] 到 [-1,0] 需要 4 秒
　　一共需要 7 秒
示例 2：

　　输入：points = [[3,2],[-2,2]]
　　输出：5
 

提示：

　　points.length == n
　　1 <= n <= 100
　　points[i].length == 2
　　-1000 <= points[i][0], points[i][1] <= 1000

 

方法一：切比雪夫距离
　　对于平面上的两个点 x = (x0, x1) 和 y = (y0, y1)，设它们横坐标距离之差为 dx = |x0 - y0|，纵坐标距离之差为 dy = |x1 - y1|，对于以下三种情况，我们可以分别计算出从 x 移动到 y 的最少次数：

　　dx < dy：沿对角线移动 dx 次，再竖直移动 dy - dx 次，总计 dx + (dy - dx) = dy 次；

　　dx == dy：沿对角线移动 dx 次；

　　dx > dy：沿对角线移动 dy 次，再水平移动 dx - dy 次，总计 dy + (dx - dy) = dx 次。

　　可以发现，对于任意一种情况，从 x 移动到 y 的最少次数为 dx 和 dy 中的较大值 max(dx, dy)，这也被称作 x 和 y 之间的 切比雪夫距离。

　　由于题目要求，需要按照数组中出现的顺序来访问这些点。因此我们遍历整个数组，对于数组中的相邻两个点，计算出它们的切比雪夫距离，所有的距离之和即为答案。

 

#include<iostream>
#include<vector>
#include<cmath>
using namespace std;
int points[100][2];

int inputValues(){
    int n;
    cout<<"enter how much pair you wannt to use"<<endl;
    cin>>n;
    for (int i = 0; i < n; i++)
    {
        cin>>points[i][0]>>points[i][1];
    }
    return n;
   
}
int minTimeToVisitAllPoints( int points[][2] ,int len) {
    int x0=points[0][0],x1 = points[0][1];
    int ans;
    for (int i = 1; i <len; i++)
    {
        int y0=points[i][0],y1=points[i][1];
        ans+=max(abs(x0-y0),abs(x1-y1));
        x0=y0;
        x1= y1;
    }
    return ans;    
}
int main(){
    int len = inputValues();
    cout<<minTimeToVisitAllPoints(points,len) ;
    
}

允许运行结果：