Diffusion Model

参考

李宏毅 2023 - Diffusion Model

概念

Diffusion

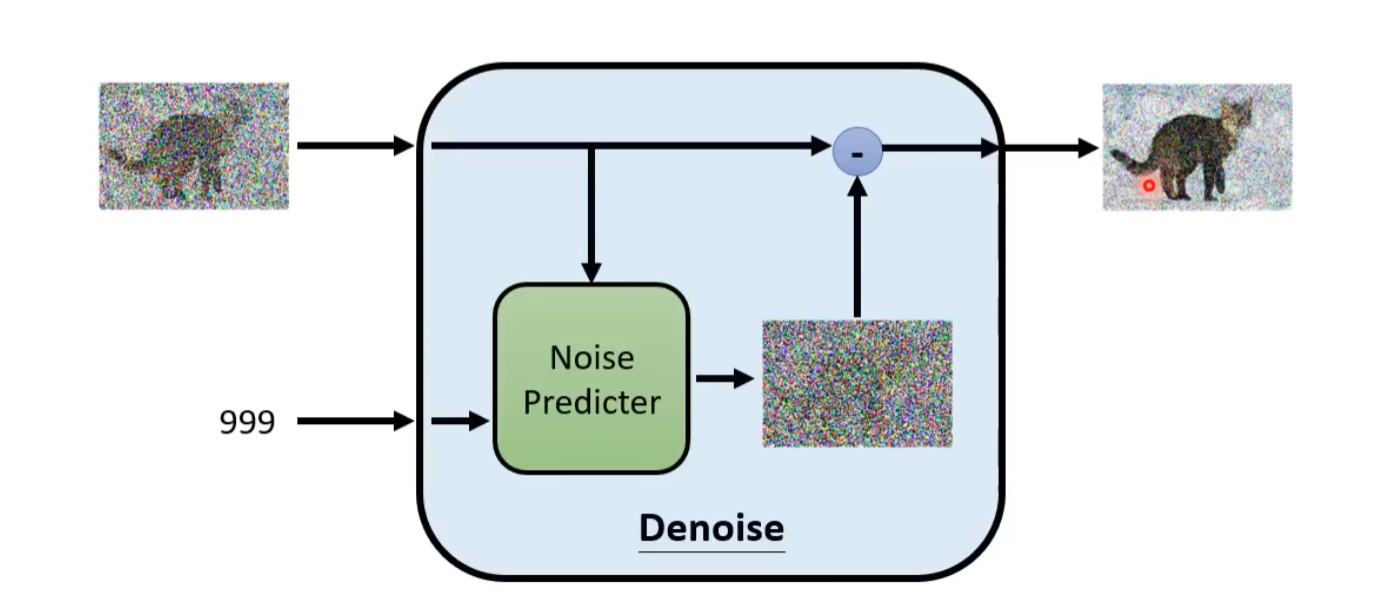
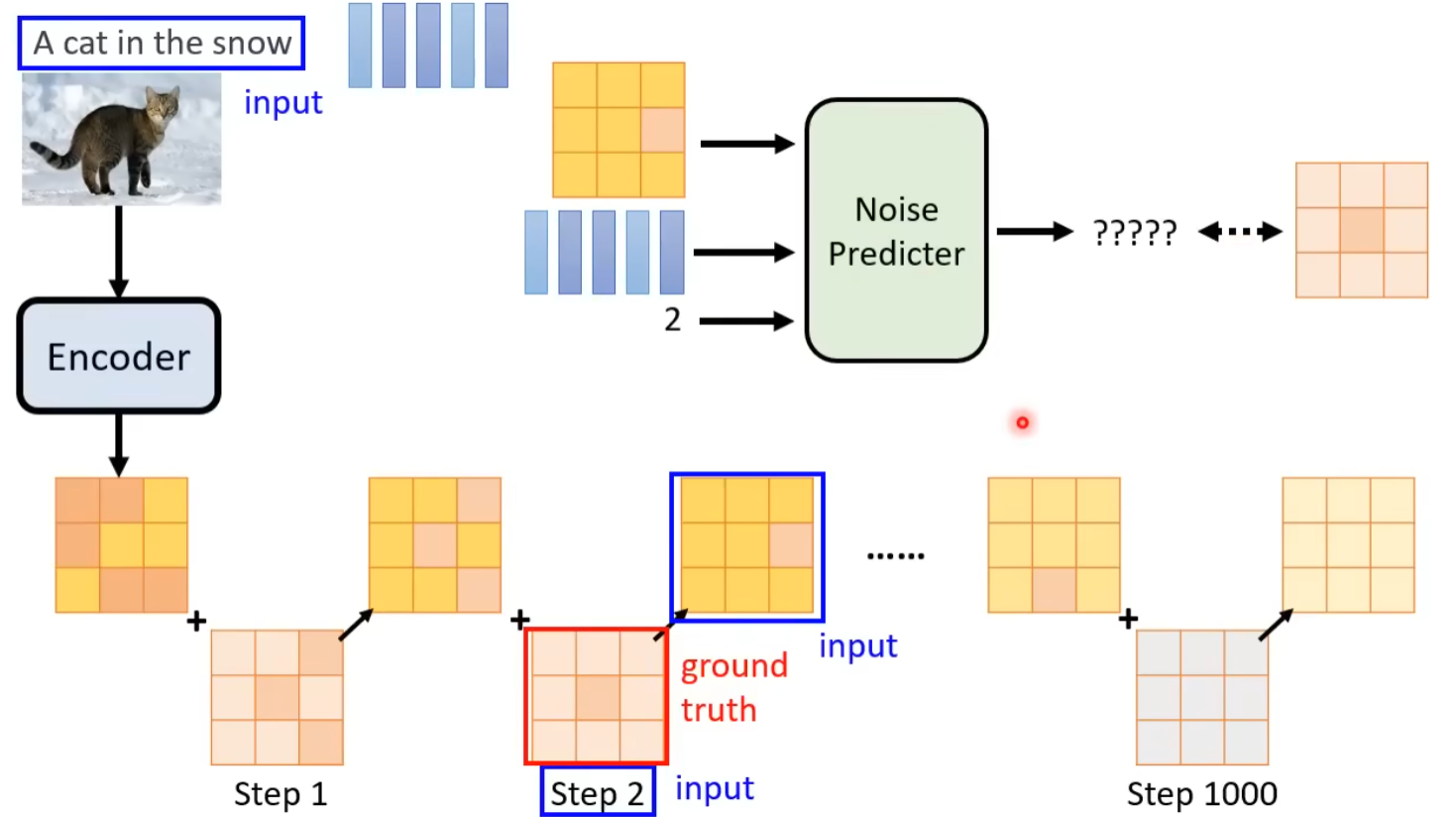
训练 N 个噪音预测器，每个预测器都是一个神经网络，每个神经网络都是一个噪音预测器

模型的 Ground Truth 来自于将原始的图片加上噪音，然后输入到神经网络中

How to Text-to-Image?

需要大量的 Text-Image Pair，比如说经典的数据来源LAION

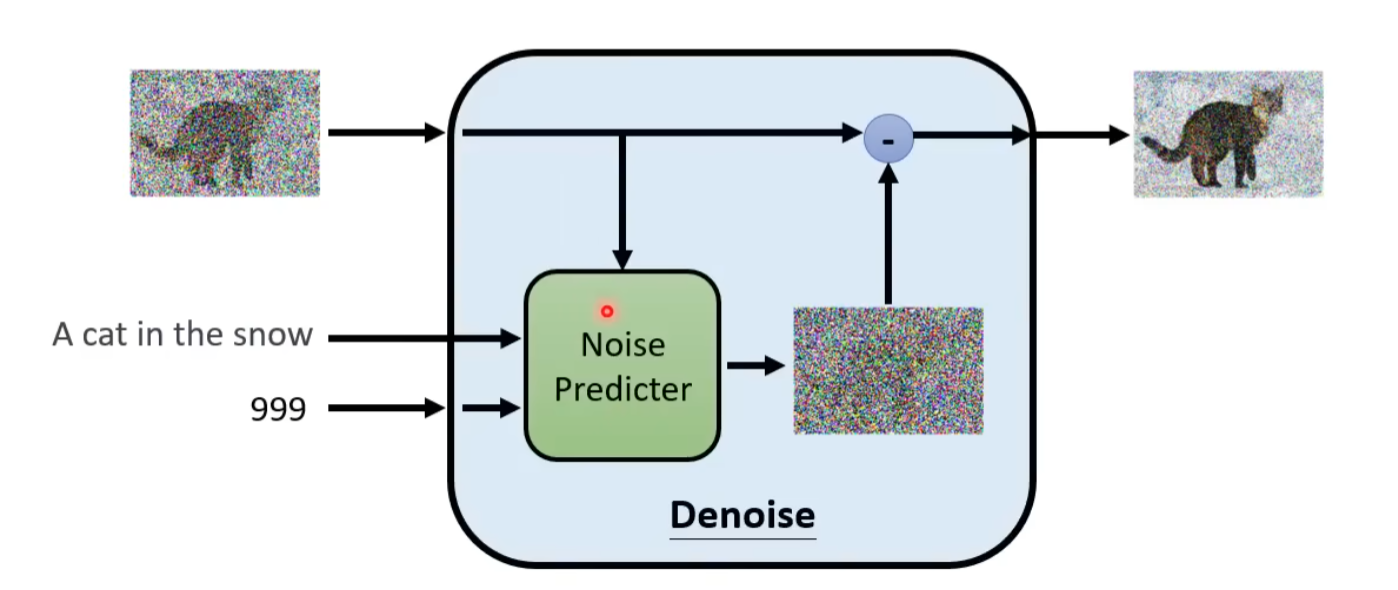
那么做到这一点非常简单，就是将 Text 加入到 Noise Predictor 中，然后训练一个噪音预测器

Stable Diffusion

需要一个 text 的 embedding，然后将这个 embedding 作为 Generation Model 的输入

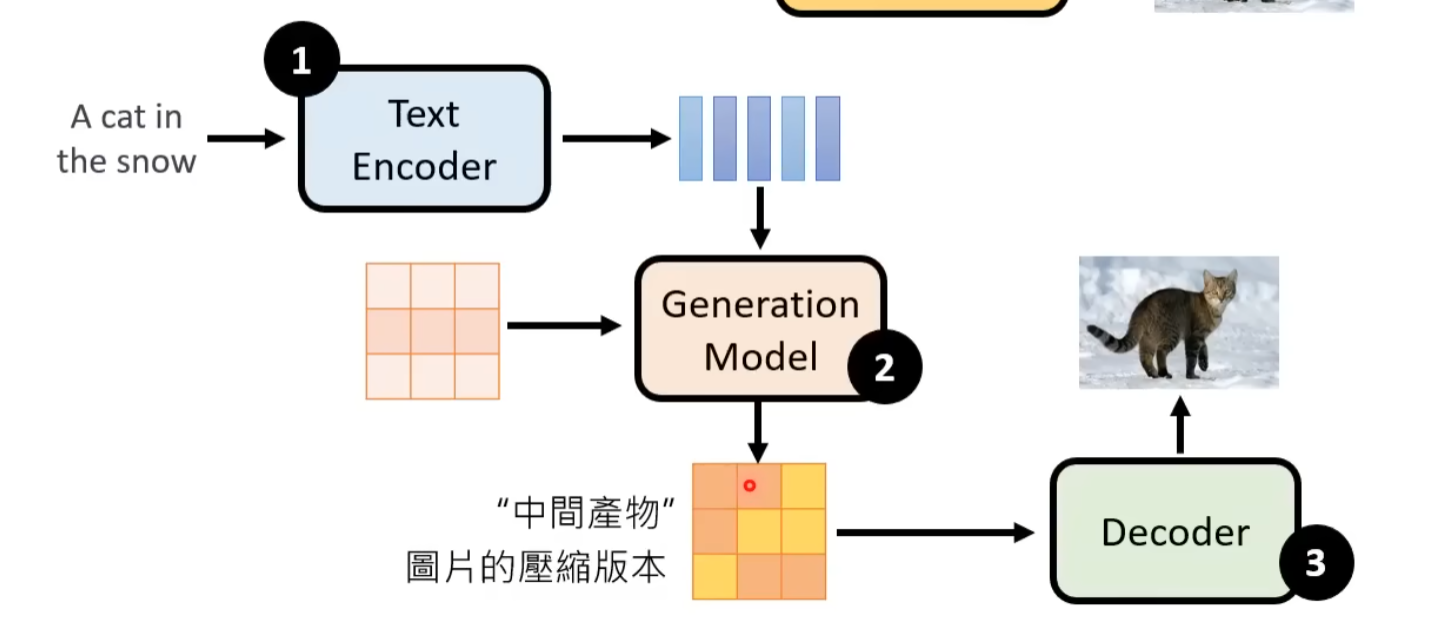
Encoder

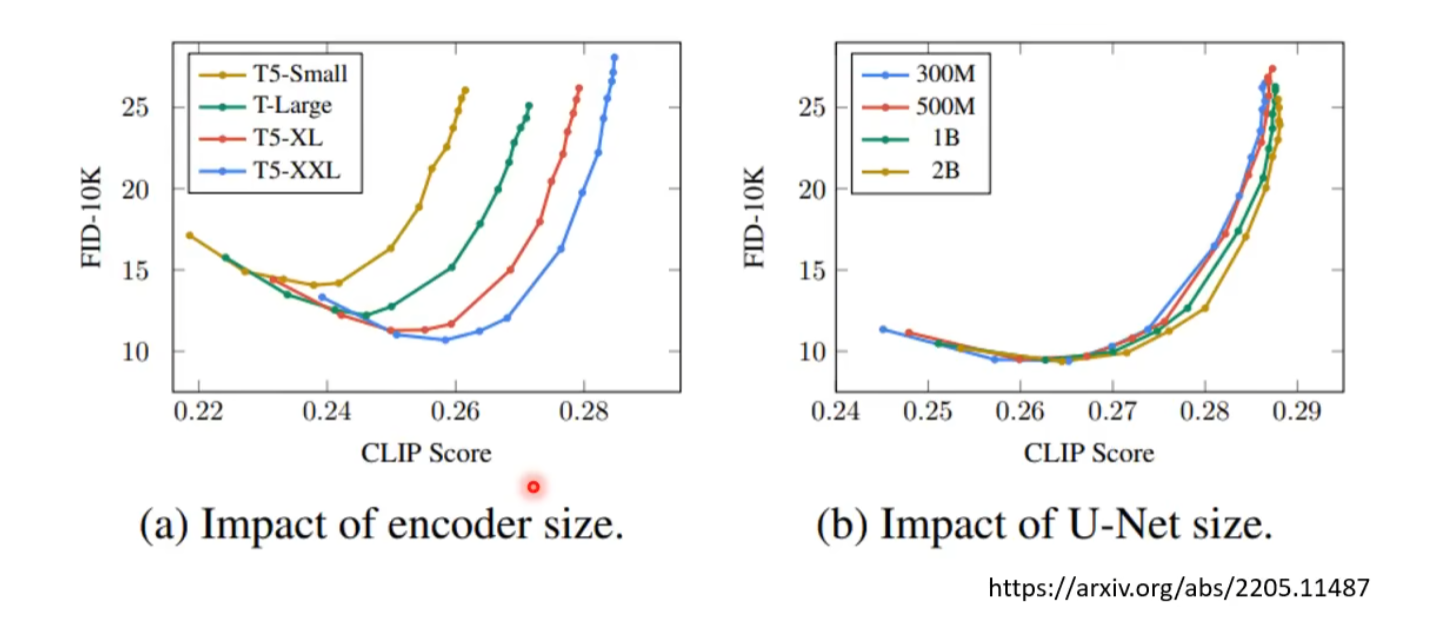
• Text Encoder 的影响

  现在可以使用 BERT、GPT 等网络生成文字的 embedding

  FID Score: 越低越好

  Clip Score: 越高越好

  

• 指标

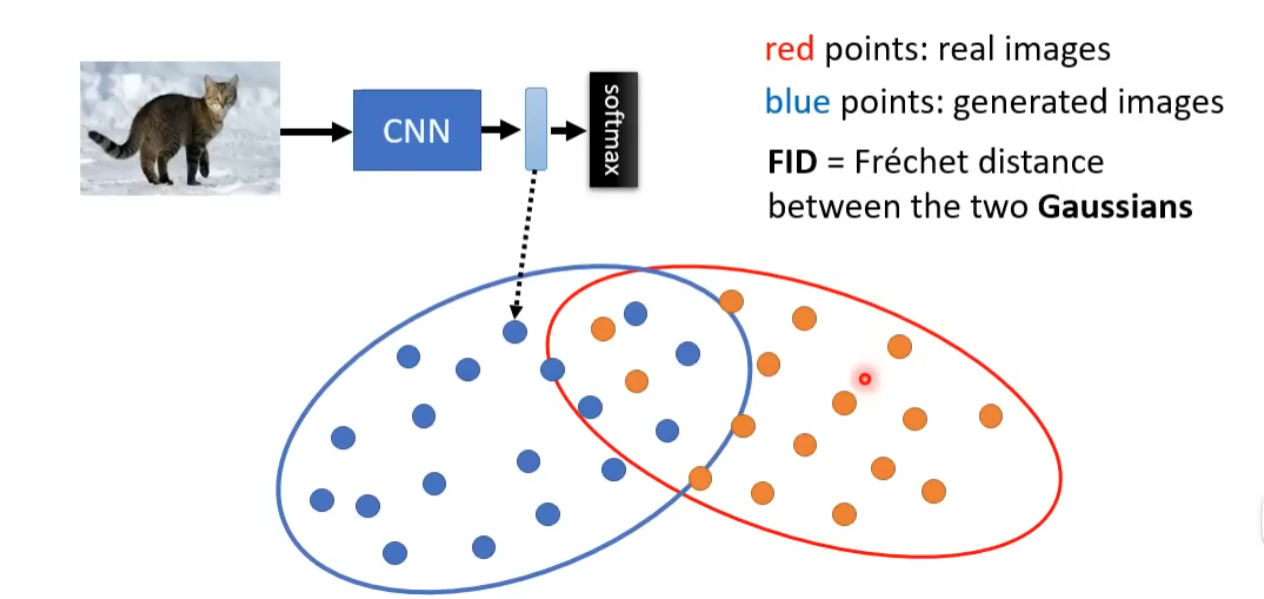
  • FID : 描绘真实图片和生成图片的距离

    假设两类表示向量的分布是高斯分布，计算两个高斯分布的距离

    需要大量的图片计量 FID

    

  • Clip Score: 用于评估生成的图片和文本的相似度

    CLIP 模型做 Text-Image Embedding 的对比学习， CLIP Score 就是这个对比学习的结果

    描述了生成的图片和文本的相似度

Decoder

训练不依赖 Text-Image Pair，仅以 Image 为输入

如果只是一个降采样的结果，实际上就是做一个 Super Resolution 的任务

如果中间产物是一个 Latent Representation，那么就是一个 AE 的任务（如何保证 latent 在同一个分布里面？）

Generator

此时的 Ground Truth 的 noise 是加入在 AE 对图片的 Encoder 后的 Latent Representation 上的

总结

• 训练 一个 Auto-Encoder，目的是为了使用到大量的没有文本配对的图片信息，然后将图片的信息转换为一个 latent representation
• 使用一个 Text Encoder，将文本转换为一个 embedding
• 训练一个 Generator，将这个 text embedding + denoise step + latent representation 转换为 ground truth 的 latent representation
  • 每一步的 ground truth 都有原始的 letent representation 加上噪音

Diffusion Model 原理

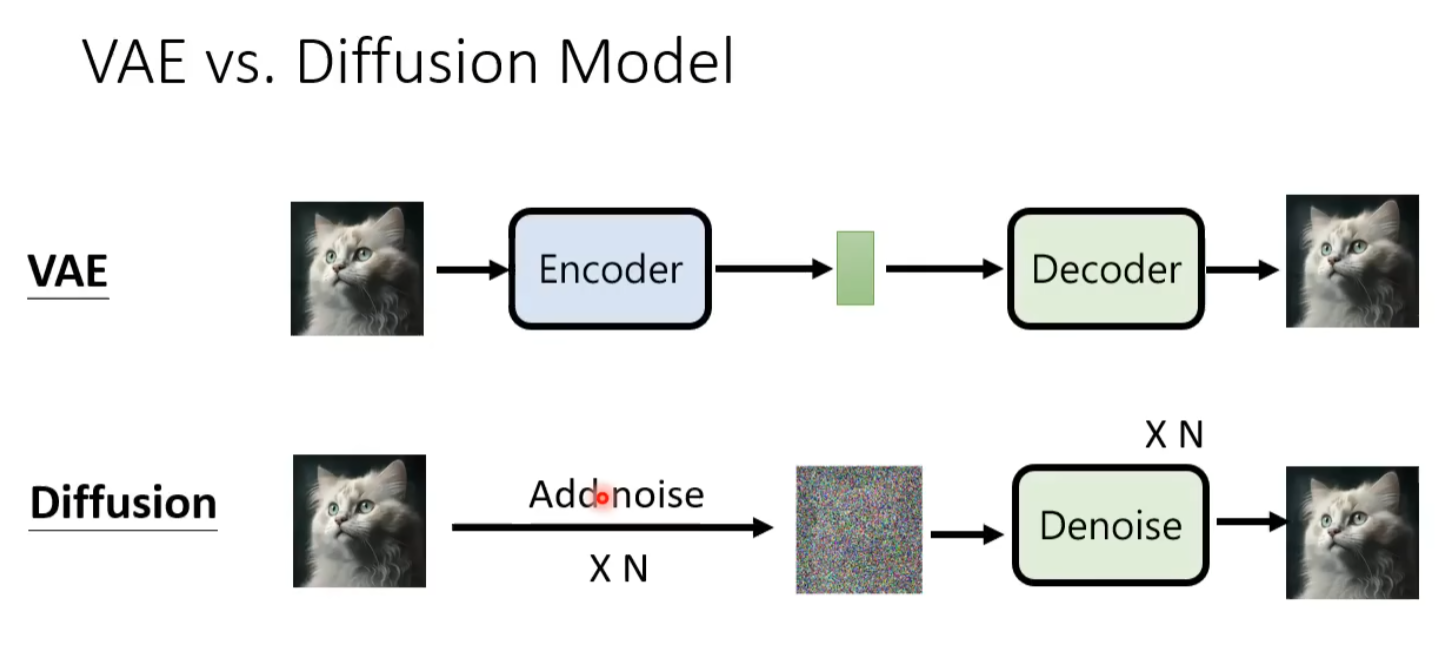
VAE 和 Diffusion Model 很相似（from 李宏毅）

DDPM-Training

• \(x_0\) 代表干净的图片
• \(t\) 代表一个加噪音的步骤数目
• \(\sqrt{\bar{a_t}}x_0 + \sqrt{1 - \bar{a_t}} \epsilon\)，代表用预先定义好的权值加权求和得出之后的 noise image， \(\bar{\alpha_1}, \dots, \bar{\alpha_T}\) 越来越小
• \(\epsilon_\theta\)，代表噪音预测器

这样训练的过程与之前介绍的 diffusion model 的训练过程不是很一样

这样训练过程直接做一次噪音，然后直接预测这个噪音，而不是像之前的 diffusion model 那样，每一步都预测噪音

DDPM-Generation

• \(z\)，每一次先生成一个噪音
• \(\frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha_t}}} \epsilon_\theta(x_t, t)\), 代表预测的噪音
• 最后还要加入一个噪音，得到最终的图片

Image Generation 的 共同目标

从简单分布采样出的随机向量\(z\)，经过生成器\(G(z)\)，得到最终想要的图片\(x\)

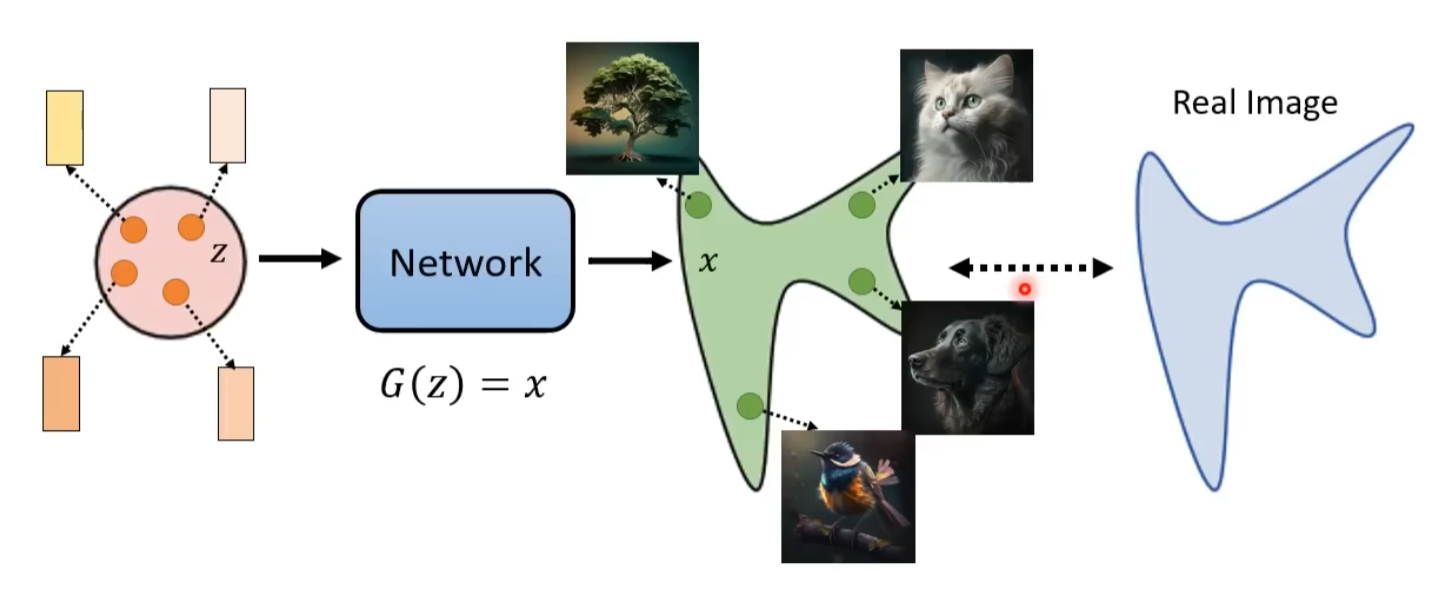
为了限制解的空间，我们需要加先验/条件，使用 Text Encoder 得到的 embedding 作为先验

为什么极大似然估计等于最小化 KL 散度？

\[\theta^* = \arg \min_\theta - \sum_{i=1}^N \log p_\theta(x_i ; \theta) \approx - \mathbb{E}_{x - p_{data}} [\log p_\theta(x ; \theta)] \\ = \arg \min_\theta - \mathbb{E}_{x - p_{data}} [\log \frac{p_\theta(x ; \theta)}{p_{data}(x)}] \\ = \arg \min_\theta - \int p_{data}(x) \log \frac{p_\theta(x ; \theta)}{p_{data}(x)} dx = \arg \min_\theta KL(p_{data} || p_\theta) \]

---

VAE

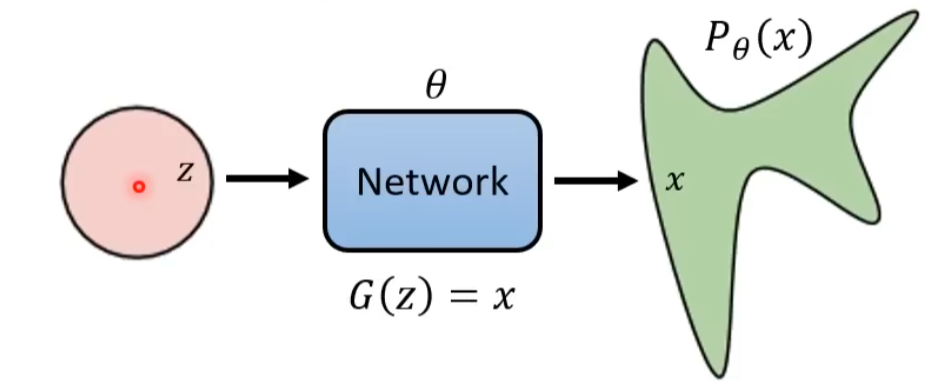
对于 VAE，\(P_\theta(x) = \int P(z) P_\theta(x|z) \text{d}z\)

但是在实际情况下，\(P_\theta(x|z) = \begin{cases} 1 & \text{if } G(z) = x \\ 0 & \text{if } G(z) \neq x \end{cases}\)

因此在 VAE 中，将\(G(z)\)视作一个高斯分布的均值，\(P_\theta(x|z) = \mathcal{N}(G(z), \sigma^2)\)

VAE 利用 EM 算法同样的思想，通过迭代求解积分

\[P_\theta(x) = P(x, z) / P(z | x) \]

\[\log P_\theta(x) = \log P(x, z) - \log P(z | x) \]

两边对\(z\)求积分

\[\log P_\theta(x) = \int_z q(z | x) \log \frac{P(x, z) }{q(z | x)}d z + \int_z q(z | x) \log \frac{q(z | x)}{P(z | x)} dz \\ \geq \int_z q(z | x) \log \frac{P(x, z) }{q(z | x)}d z = \mathbb{E}_{z \sim q(z | x)} [\log \frac{P(x, z) }{q(z | x)}] \]

我们不需要关心\(q(z|x)\) 的具体形式，只需要关心 KL 散度的最小值，因此我们可以通过变分推断的方法，先最小化 KL 散度，然后再最大化 Lower Bound

DDPM

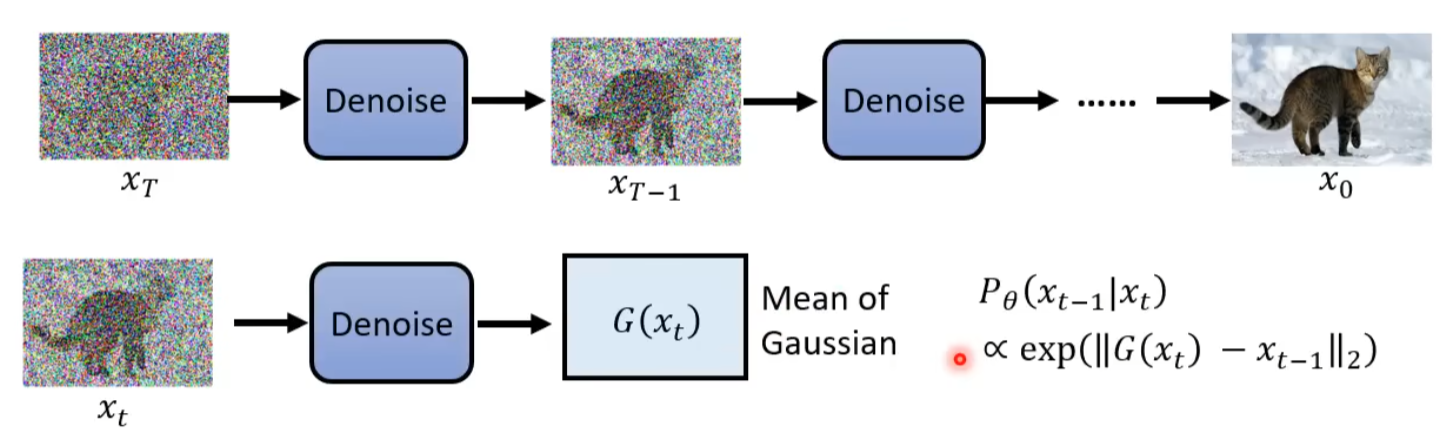
假设具有马尔可夫性质，\(P(x_0, \dots, x_T) = P(x_T) \prod_{t=1}^{T} P(x_{t-1} | x_{t})\)

那么我们可以得到

\[P_\theta(x_0) = \int P(x_0, x_1, \dots, x_T) \text{d}x_1 \dots \text{d}x_T \\ = \int P(x_T) \prod_{t=1}^{T} P(x_{t-1} | x_{t}) \text{d}x_1 \dots \text{d}x_T \]

DDPM:

\[\max \mathbb{E}_{q(x_1, \dots, x_T | x_0)} [\log P(x_0, x_1, \dots, x_T)] - \mathbb{E}_{q(x_1, \dots, x_T | x_0)} [\log q(x_1, \dots, x_T | x_0)] \]

为了求解 q，我们用如下的方法

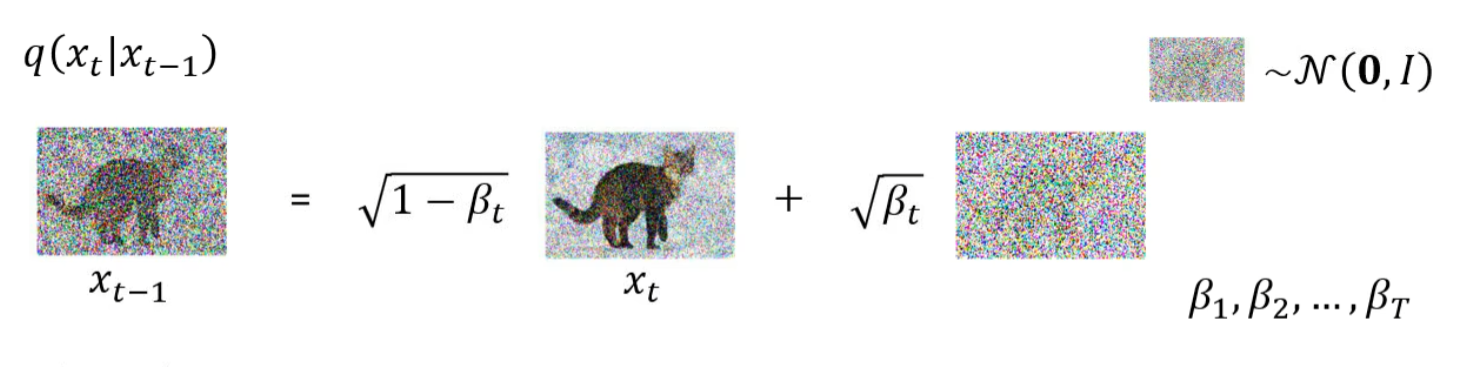
求解 q 不需要一个序列的数据，因为序列的数据合并起来等同于采样一个噪声

---

求解变分：Understanding Diffusion Models: A Unified Perspective

这一段在说明从 Diffusion 原始 IDEA 到算法描述的过程，以后再来看