ch11 特征选择与稀疏学习

子集选择与评价

缓解维度灾难的另一种重要方法是进行特征筛选，同时它也能降低学习任务的难度，只留下关键特征。

对当前学习任务有用的属性称为“相关特征”，而对当前学习任务没有用的属性称为“无关特征”，包含信息能被其他特征表示的属性称为“冗余特征”。

如果想要从原始特征集中选择出一个子集，那么就是一个特征选择问题。特征选择通常包含以下两个环节

• 子集搜索：搜索最优特征子集
  暴力搜索会遇见组合爆炸问题，所以需要一些启发式方法，如贪心法（前向、后向、双向）

• 子集评价：评价特征子集的好坏
  评价指标有很多，如信息增益、信息增益比、基尼指数、方差、相关系数等

常见的特征选择方法有：过滤法、包裹法、嵌入法

过滤法

先对数据集进行特征选择，再用特征子集训练模型，特征选择过程与学习过程无关

著名的算法有：Relief、Relief-F

Relief 设计了一个相关统计量用于度量特征的重要性

相关统计量：对于每一个样本点$x_i$，寻找与其最近邻的样本点$x_{i,nh}$（同类）和$x_{i,nm}$（异类），于是我们可以定义如下的相关统计量

$$\delta^j = \sum_{i=1}^m - \text{diff}(x_{i,j}, x_{i,nh,j})^2 + \text{diff}(x_{i,j}, x_{i,nm,j})^2$$

那么最终得到的一个统计量向量越大，说明子集选择的越好，分类性能越强

包裹法

直接利用学习器的性能来评价特征子集的好坏，通常效果更好，但计算开销也更大

著名的算法有：LVW 框架，在特征选择的过程中使用了随机算法

嵌入法

将特征选择过程与学习过程融为一体，直接在学习器上进行特征选择

著名的算法有： L1 正则化、L2 正则化

对于线性回归算法，我们通常认为有这样一条直线可以拟合数据

$$Y = XW$$

当$X$不可逆时，我们使用最小二乘法，即

$$\min \| Y - XW \|_2^2$$

$$W = (X^T X)^{-1} X^T Y$$

当$X$列不满秩时，即$X^T X$不可逆，即样本特征多于样本数，此时我们可以使用正则化

$$\min \| Y - XW \|_2^2 + \lambda \| W \|_2^2$$

$$W = (X^T X + \lambda I)^{-1} X^T Y$$

保证了$X^T X + \lambda I$可逆，从而解决了多重共线性问题

这是一种罚函数法，即在目标函数中加入了一个罚函数，使得优化问题变得更加复杂

最直观的罚函数是 L0 范数，即非零元素的个数，但是 L0 范数是一个非凸函数，所以我们通常使用 L1 范数，L1 通常能获得稀疏解，即有些特征的权重为 0

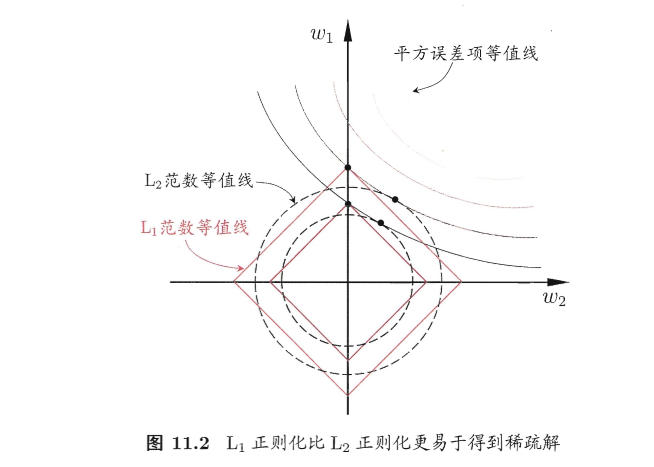
因此可以说，L1 正则化是一种特征选择方法

L1 正则化的求解方法

可以使用近端梯度下降法（Proximal Gradient Descent），对于优化目标

$$\min_x f(x) + \lambda \| x \|_1$$

如果满足 Lipschitz 连续梯度条件，希望$\nabla f$不要变化太快，即

$$\exist L > 0, \quad \| \nabla f(x) - \nabla f(y) \|_2 \leq L \| x - y \|_2, \quad \forall x, y \\ \iff \frac{\| \nabla f(x) - \nabla f(y) \|}{\| x - y \|} \leq L \\ \Rightarrow \nabla^2 f(x) \preceq L$$

那么在$x_k$处对目标函数进行二阶泰勒展开，有

$$f(x) \approx f(x_k) + \nabla f(x_k)^T (x - x_k) + \frac{L}{2} \| x - x_k \|_2^2 \\ = \frac{L}{2} \| x - (x_k - \frac{1}{L} \nabla f(x_k)) \|_2^2 + \text{const}$$

那么我们可以得到

$$x_{k+1} = \arg \min_x \frac{L}{2} \| x - (x_k - \frac{1}{L} \nabla f(x_k)) \|_2^2 \\ \Rightarrow x_{k+1} = x_k - \frac{1}{L} \nabla f(x_k)$$

最小值可以通过如上的迭代方式求解，即梯度下降法是对 二次拟合函数的近似

那么应用到 L1 正则化的问题上，我们可以得到

$$x_{k+1} = \arg \min_x f(x_k) + \nabla f(x_k)^T (x - x) + \frac{L}{2} \| x - x_k \|_2^2 + \lambda \| x \|_1 \\ \Rightarrow x_{k+1} = \arg \min_x \frac{L}{2} \| x - (x_k - \frac{1}{L} \nabla f(x_k)) \|_2^2 + \lambda \| x \|_1$$

这个问题不存在交叉项，因此可以使用坐标轴下降法（Coordinate Descent）求解，即

$$x_i^{(k+1)} = \arg \min_{x_i} \frac{L}{2} (x_i - z_i^{k})^2 + \lambda |x_i|$$

求导数，令导数为 0，即可得到

$$x_i^{(k+1)} = \begin{cases} z_i^{(k)} - \frac{\lambda}{L}, & z_i^{(k)} > \frac{\lambda}{L} \\ 0, & |z_i^{(k)}| \leq \frac{\lambda}{L} \\ z_i^{(k)} + \frac{\lambda}{L}, & z_i^{(k)} < -\frac{\lambda}{L} \end{cases}$$

L1 正则化的求解方法

字典学习与稀疏表示

学习到整个数据矩阵的稀疏性

$$\min{B, \alpha_i} \sum_{i=1}^m \| x_i - B \alpha_i \|_2^2 + \lambda \| \alpha_i \|_1 \\ \iff \min_{B, A} \| X - BA \|_F^2 + \lambda \| A \|_1$$

可以使用 PGD 类似的思想交替优化$B, A$

• Step 1：固定$B$, 求解$A$

$$\min_{\alpha_i} \| x_i - B \alpha_i \|_2^2 + \lambda \| \alpha_i \|_1$$

• Step 2：固定$A$, 求解$B$

$$\min_B \| X - BA \|_F^2$$

这个问题可以通过 SVD 分解求解，即每一步固定其他$B$中的列，求解$B$中的一列，$\min_{b_i} \| E_i - b_i\alpha^i \|_F^2$